Производные и дифференциалы высших порядков

Если функция y = f (x) дифференцируема на некотором промежутке, то она имеет на этом промежутке производную y ' = f ’(x), которая в свою очередь, может иметь производную: (y ')' = (f ’(x))' = y '', называемая второй производной для функции y = f (x). Она обозначается:

Может случиться, что новая функция y ''(x) имеет производную, она называется третьей производной для функции y = f (x). Ее обозначения:

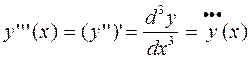
Производная “n”-ого порядка функции y = f (x) обозначается:

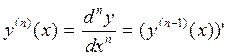
Вторым дифференциалом функции y = f(x) в точке x называется выражение, обозначаемое d² y и вычисляемое по формуле:

,

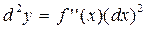если x – независимая переменная.

Дифференциал третьего порядка функции y = f (x):

,

если x – независимая переменная. И так далее.

Замечание: дифференциал уже второго порядка не обладает свойством инвариантности формы.