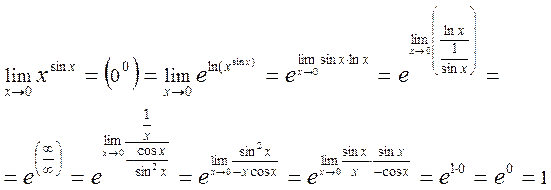Свойства функций, непрерывных на отрезке

Теорема 1. Если функция f (x) на отрезке [ a; b ] непрерывна, то она достигает на этом отрезке своих наименьшего m и наибольшего M значений, то есть для любых x Î [ a; b ] выполняется неравенство:

m ≤ f (x) ≤ M.

Теорема 2. Если функция f (x) на отрезке [ a; b ] непрерывна, то для любого числа С, удовлетворяющего неравенству m ≤ С ≤ M, на отрезке [ a; b ], найдется хотя бы одна точа х _о, в которой выполняется равенство:

f (х _о) = С.

Теорема 3. Если функция f (x) на отрезке [ a; b ] непрерывна и на концах этого отрезка имеет значения различных знаков, то существует хотя бы одна точка х _оÎ (a; b), в которой выполняется равенство:

f (х _о) = 0.

Теорема 4 (теорема Ролля)

Если функция f (x) определена на [ a; b ] и выполнены следующие условия:

1. f (x) непрерывна на [ a; b ];

2. f (x) дифференцируема на (a; b);

3. f (a) = f (b),

то внутри этого отрезка найдется хотя бы одна точка х _о, в которой выполняется равенство:

f ' (х_о) = 0.

Доказательство. Так как f (x) непрерывна на [ a; b ], то она достигает на этом отрезке своих наименьшего m и наибольшего M значений.

Возможны два случая:

1) m = M,

2) m < M.

1) Если m = M, то f (x) = const = m = M. Тогда f '(x) = 0 при любом x Î (a; b).

Следовательно, в этом случае теорема верна и при этом в качестве х _о можно рассматривать любое значение x Î (a; b).

2) Если m < M, то, исходя из условия f (a) = f (b), по крайней мере одно из чисел m или M не равно f (a) = f (b). Для определенности предположим, что M – наибольшее значение f (x) достигается не на концах отрезка [ a; b ], а в некоторой внутренней точке х _о Î (a; b). Тогда в точке х _о для приращения функции справедливо неравенство: D y = f (х _о + D x) - f (х _о) ≤ 0, так как f (х _о) = M – наибольшее значение f (x) на [ a; b ] и D x такое, что х _о + D x Î [ a; b ].

· Если D x > 0, то 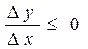и существует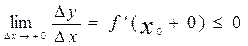

· Если D x < 0, то и существует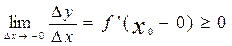

Так как по условию теоремы функция f (x) дифференцируема при x Î (a; b), то b в точке х _о существует производная. Значит справедливы равенства:

f ' (х _о +0) = f ' (х _о -0) = f ' (х _о) = 0.

Теорема доказана.

Геометрический смысл теоремы Ролля

С геометрической точки зрения терема Ролля означает, что график функции, непрерывной на отрезке [ a; b ], дифференцируемой на интервале (a; b) и принимающей на концах отрезка равные значения, имеет хотя бы одну точку (х _о ; f (х _о)), где х _оÎ (a; b), в которой касательная параллельна оси O x (рис.7)

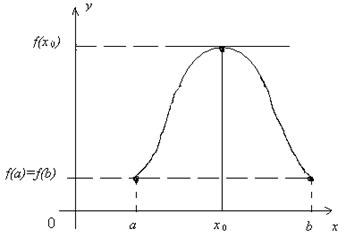
Рис. 7

Теорема 5 (теорема Лагранжа).

Если функция f (x) определена на [ a; b ] и выполнены следующие условия:

1) f (x) непрерывна на отрезке [ a; b ],

2) f (x) дифференцируема на интервале (a; b), то внутри этого отрезка существует хотя бы одна точка х _о, в которой выполняется равенство:

f ' (х_о) = .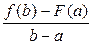

Доказательство: Рассмотрим вспомогательную функцию F (x) = f (x) + l× x, где l = const. Потребуем, что бы для F (x) выполнялось условие F (a) = F (b).

Так как F (a) = f (a) + l × a; F (b) = f (b) + l × b, то получим равенство:

f (a) + l × a = f (b) + l × b.

Отсюда выразим значение l:

l = - .

При этом значении l функция F (x) = f (x) - .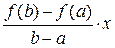

Функция F (x) удовлетворяет всем условиям теоремы Ролля:

F (x) непрерывна на [ a; b ]:

F (x) дифференцируема на (a; b)

F (a) = F (b).

Следовательно, по теореме Ролля на (a; b) существует хотя бы одна точка х _о, в которой выполняется равенство:

F ' (х _о) = 0.

Найдем F '(x):

F ' (x) = f '(x) -

Поэтому F ' (x) = f ' (х_о) -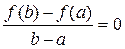

=> f ' (х_о) =

Теорема доказана.

Геометрический смысл теоремы Лагранжа

С геометрической точки зрения теорема Лагранжа означает, что график функции, непрерывной на отрезке [ a; b ] и дифференцируемой на интервале (a; b), имеет хотя бы одну точку (х _о; f (х _о), в которой касательная параллельна секущей, проходящей через точки A (a; f (a)) и B (b; f (b)) (рис.8)

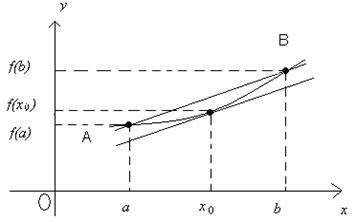
Рис. 8

Теорема 6 (теорема Коши).

Если функции f (x) и g (x) определены на отрезке [ a; b ] и удовлетворяют условиям:

1) f (x) и g (x) непрерывны на [ a; b ];

2) f (x) и g (x) дифференцируемы на (a; b);

3) g ' (x) ¹ 0 при любом x Î (a; b),

то внутри отрезка [ a; b ] найдется хотя бы одна точка х _о, в которой выполняется равенство:

Доказательство аналогично доказательству теоремы 5 при вспомогательной функции

F (x) = f (x) + l × g (x),

где l = const, которую выбирают так, чтобы F (a) = F (b).

Теорема 7 (правило Лопиталя).

Если функции f (x) и g (x) определены в некоторой окрестности точки х _о и в этой окрестности они удовлетворяют условиям:

1) f (x) и g (x) дифференцируемы в каждой точке, за исключением, может быть, самой точки х _о;

2) g ' (x) ¹ 0 для любого x из этой окрестности;

3) 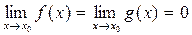или

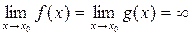
тогда, если существует конечный или бесконечный, то выполняется равенство:

= .

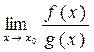Замечание 1. Это правило Лопиталя используется для раскрытия неопределенностей типа 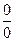или 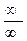, возникающих при вычислении пределов. Если под знаком предела оказывается неопределенность другого типа: 0× ∞, ∞ - ∞, 1⁰, 0⁰ или ∞ ⁰, то с помощью тождественных алгебраических преобразований такая неопределенность приводится к 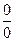или 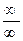, а затем можно применить правило Лопиталя.

Замечание 2. Если к условиям теоремы 6 добавить дифференцируемость функций f '(x) и g '(x) в окрестности точки х _о, то при выполнении остальных требований для f '(x) и g '(x) правило Лопиталя можно применить повторно. При этом будет справедливо равенство:

= =

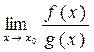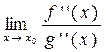
Пример 1. Вычислить предел:

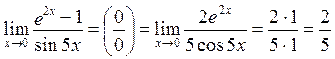
Пример 2. Вычислить предел:

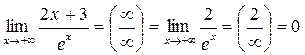
Пример 3. Вычислить предел:

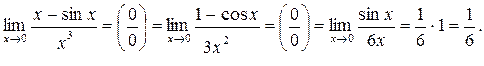
Пример 4. Вычислить предел:

.

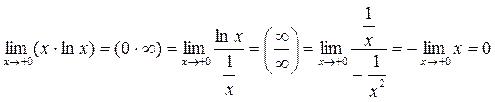Пример 5. Вычислить предел:

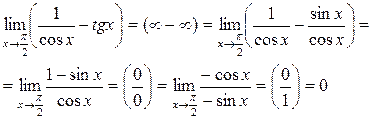
Пример 6. Вычислить предел: