
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Схема исследования функции. Построение графика
|
|
(слайды 8, 9 и 10 в презентации)
1) Найти область определения функции y = f (x) – множество D(f) тех значений x, при которых y = f (x) имеет смысл.
2) Исследовать функцию на периодичность: выяснить, существует ли наименьшее положительное число T, что
f (x +T) = f (x) для любого x Î D(f).
Если «да», то целесообразно далее исследовать функцию и строить ее график только на некотором отрезке длиной периода T.
Затем продолжить график на всю область определения, разбивая ее на интервалы длины T, в которых повторяется картинка графика.
3) Исследовать функцию на четность и нечетность: выяснить, выполняются ли равенства:
f (- x) = f (x) для любого x Î D(f) – четность,
или f (- x) = - f (x) для любого x Î D(f) – нечетность.
Это позволяет узнать есть ли симметрия графика:
относительно оси O y – четная
или относительно начала координат – нечетная.
4) Найти точки пресечения графика функции с осями координат:
а) с осью O y: точка (0; f (o)), если OÎ D(f),
б) с осью O y: точка (x k; 0), где x kÎ D(f) и является решением уравнения f (x) = 0.
5) Найти промежутки знакопостоянства: выяснить, при каких x Î D(f) выполняются неравенства f (x) > 0 (при этом график функции расположен выше оси O x) и f (x) < 0 (при этом график функции расположен ниже оси O x).
6) Исследовать функцию на непрерывность, установить тип точек разрыва (см. §6, п.1).
7) Найти вертикальные и наклонные асимптоты (см. §6, п.1).
8) Найти промежутки убывания и возрастания, экстремумы функции (см. §6, п.2 и п.3).
9) Найти множество E(f) значений функции.
10) Найти промежутки выпуклости, вогнутости и точки перегиба графика (см. §6, п.4).
11) Построить график функции, используя свойства, установленные в проведенном исследовании. Если в некоторых промежутках график остался неясным, то его уточняют по дополнительным точкам.
Пример. Исследовать функцию y = (x +2) e - x и построить ее график.
1) D(y) = R.
2) Функция не периодическая.
3) Так как y (- x) # y (x) и y (- x) # - y (x), то функция общего вида, не является ни четной, ни нечетной.
4) Точка пересечения графика
с O x: (-2; 0), с O y: (0; 2)
5) При x Î (-¥; -2) функция отрицательная,
при x Î (-2; +¥) функция положительная.
6) Функция непрерывна при x Î R.
7) Вертикальных асимптот нет.
Наклонные асимптоты: y = k x + b.
а) 
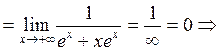 k=0 при x®+¥
k=0 при x®+¥
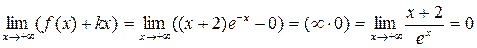 .
.
b=0 при x®+¥.
Следовательно, y = 0 – наклонная (горизонтальная) асимптота при x ®+¥.
б) 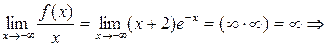
при x ®-¥ наклонной асимптоты нет.
8) f ’(x) = ((x +2) e - x )’ = 1× e - x +(x +2)× (- e - x ) = e - x (1- x -2) = -(x +1) e - x .
D(y ’) = R.
y ’ = 0: -(x +1) e - x = 0 Þ x = -1, f (-1) = 1× e 1 = e.
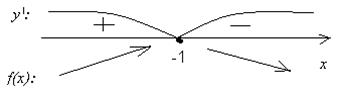
при x Î (-¥; -1) f (x) возрастает,
при x Î (-1; +¥) f (x) убывает,
при x = -1 f m ax (-1) = (-1+2) e -(-1) = e.
9) E(f) = (-¥; e), так как
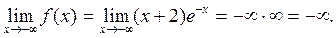

и f m ax (-1) = e.
10) f ”(x) = (-(x +1) e - x)’ = -1 e - x +(x +1) e - x = e - x (x +1-1) = xe - x.
D(f ”) = R
f ”(x) = 0: xe - x = 0 Þ x = 0, f (0) = 2.
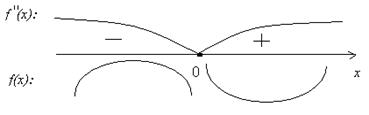
при x Î (-¥; 0) график f (x) выпуклый
при x Î (-(0; +¥) график f (x) вогнутый
Точка (0; 2) – точка перегиба графика.
11) Сведем результаты проведенного исследования в таблицу и построим график (рис. 12)
| x | -¥; -1 | -1 | -1; 0 | 0; +¥ | |
| знак f ’(x) | + | - | - | - | |
| знак f ”(x) | - | - | - | + | |
| F (x) | e | ||||

| 
| 
| 
| 
|
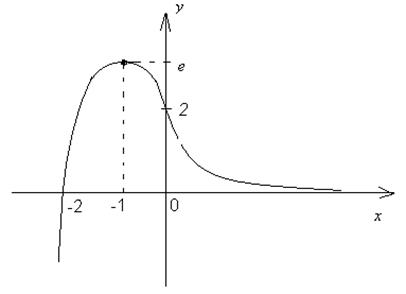
Рис. 12