Выпуклость, вогнутость и точки перегиба графика функции

Пусть функция y = f (x) дифференцируема в любой точке промежутка (a; b). Тогда она имеет конечную производную в любой точке этого промежутка. Значит, существует касательная к графику функции y = f (x) в любой его точке (x; f (x)), a < x < b.

Определение 8. График функции y = f (x), дифференцируемой в каждой точке промежутка (a; b) называется выпуклым (вогнутым) на этом промежутке, если для любого x Î (a; b) график расположен не выше (не ниже) касательной к графику в точке (x; f (x)) (слайд 7 в презентации).

Теорема 5 (достаточное условие выпуклости или вогнутости кривой).

Пусть функция y = f (x) дважды дифференцируема на промежутке (a; b) и f ”(x) для x Î (a; b) сохраняет свой знак, то кривая y = f (x) выпуклая, если f ”(x) £ 0 при x Î (a; b), и кривая y = f (x) вогнутая, если f ”(x) ³ 0 при x Î (a; b).

Доказательство. Для определенности рассмотрим случай, когда f ”(x) ³ 0 для x Î (a; b). Обозначим x ₀ любую точку промежутка (a; b). Построим касательную к кривой y = f (x) в точке (x ₀; f (x ₀)): y _касат = f (x ₀) + f (x ₀)(x - x ₀). Покажем, что график функции y = f (x) лежит не ниже этой касательной, то есть выполняется неравенство (рис.11):

f (x) – y _касат. (x) ³ 0 для любого x Î (a; b).

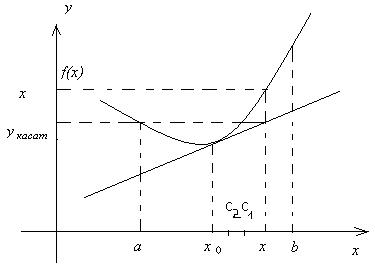
Рис. 11

f (x) – y _касат(x) = f (x) – (f (x ₀) + f ’(x ₀)(x - x ₀)) =

= f (x) – f (x ₀) – f ’(x ₀)(x - x ₀) = (f (x) - f (x ₀)) - f ’(x ₀)(x - x ₀), где x Î (a; b), (1)

На [ x ₀; x ] функция y = f (x) удовлетворяет условию теоремы Лагранжа. То есть на [ x ₀; x ] найдется хотя бы одна точка c₁, для которой выполняется равенство:

F (x) – f (x ₀) = f ’(c₁)(x - x ₀).

Поставим в равенство (1) полученное соотношение:

f (x) – y _касат(x) = f ’(c₁)(x - x ₀) – f ’(x ₀)(x - x ₀) = (x - x ₀)× (f ’(c₁) – f ’(x ₀)). (2)

На [ x ₀; c₁] функция f ’(x) удовлетворяет условию теоремы Лагранжа. То есть на (x ₀; c₁) найдется хотя бы одна точка с₂, для которой выполняется равенство:

f ’(c₁) – f ’(x ₀) = f ”(c₂)(c₁- x ₀).

Подставим в равенство (2) полученное соотношение:

f (x) – y _касат(x) = (x - x ₀)× f ”(c₂)(c₁- x ₀). (3)

Если x > x ₀, то c₁ > x ₀ и c₂ > x ₀, то есть x - x ₀ < 0 и с₁- x ₀ < 0.

По предположению f ”(x) ³ 0. Тогда f (x) – y _касат(x) ³ 0.

Если x < x ₀, то c₁ < x ₀ и c₂ < x ₀, то есть x - x ₀ > 0 и c₁- x ₀ > 0.

Тогда f (x) – y _касат(x) ³ 0.

Следовательно, при любом x Î (a; b) выполняется неравенство:

f (x) – y _касат(x) ³ 0.

Аналогично можно доказать, что если f ”(x) £ 0 при любом x Î (a; b), то кривая y = f (x) на (a; b) будет выпуклой.

Теорема доказана.

Определение 9. Пусть в точке (x ₀; f (x ₀)) существует касательная. Тогда точка (x ₀; f (x ₀)), отделяющая выпуклую часть кривой от вогнутой или наоборот называется точкой перегиба графика функции y = f (x).

Теорема 6 (достаточное условие точки перегиба).

Если функция y = f (x) дифференцируема в окрестности точки x _0, вторая производная функции f ”(x ₀) = 0 или не существует и f ”(x) меняет свой знак при переходе x через точку x ₀, то точка (x ₀; f (x ₀)) – точка перегиба кривой y = f (x).

Доказательство. Для определенности рассмотрим слeчай, когда f ”(x) при переходе через точку x ₀ изменяет знак с «+» на «-».

Тогда в левой полуокрестности точки x ₀ f ”(x) > 0, то есть кривая при x < x ₀ вогнутая, а в правой полуокрестности точки x ₀ f ”(x) < 0, то есть кривая при x > x ₀ выпуклая.

Следовательно, точка (x ₀; f (x ₀)) по определению является точкой перегиба графика функции y = f (x).

Аналогично рассматривается другой случай, когда f ”(x) при переходе через точку x ₀ изменяет знак с «-» на «+».

Теорема доказана.