Асимптоты плоской кривой

Определение 1. Если точка M(x; y) перемещается по кривой y = f (x) так, что хотя бы одна из координат точки стремиться к ¥ и при этом расстояние от этой точки до некоторой прямой стремиться к 0, то эта прямая называется асимптотой кривой y = f(x).

Асимптоты бывают двух видов: вертикальные и наклонные.

Определение 2. Прямая x = a называется вертикальной асимптотой кривой y = f (x), если хотя бы один из односторонних пределов

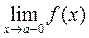или

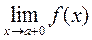
равен +¥ или -¥

Замечание. Если прямая x = a является вертикальной асимптотой кривой y = f (x), то в точке x = a функция f (x) имеет разрыв второго рода. Наоборот. Если в точке x = a функция f (x) имеет разрыв второго рода, то прямая x = a является вертикальной асимптотой кривой y = f (x).

Определение 3. Прямая y = k x + b называется наклонной асимптотой кривой y = f (x) при x ®+¥ (или x ®-¥), если функцию f (x) можно представить в виде:

,

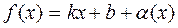где a(x) – бесконечно малая функция при x ®+¥ (или x ®-¥).

Теорема 1. Для того чтобы кривая y = f (x) имела наклонную асимптоту при x ®+¥ (или x ®-¥) необходимо и достаточно существования двух конечных пределов:

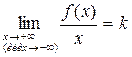и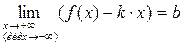

Доказательство. Ограничимся случаем x ®+¥.

Необходимость. Пусть y = k x + b – наклонная асимптота при x ®+¥ кривой y = f (x). Тогда функция f (x) представима в виде:

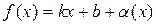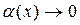, где при .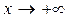

Убедимся в существовании конечных пределов:

.

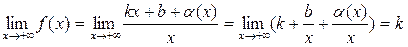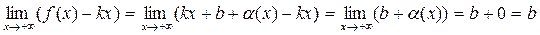
необходимость доказана.

Достаточность. Пусть существуют конечные пределы 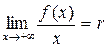и .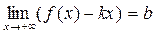

Тогда по свойству конечных пределов второй предел можно переписать в виде:

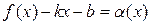, где a(x) – бесконечно малая при x ®+¥.

Отсюда получаем:

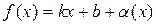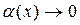, где при .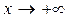

Достаточность доказана.

Пример 1. Найти асимптоты кривой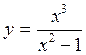

Решение.

1) D(y) = (-¥; -1) È (-1; 1) È (1; + ¥).

2) Точки x = -1 и x = 1 являются точками разрыва второго рода, так как:

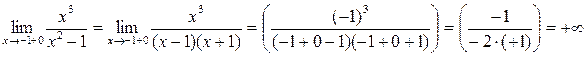
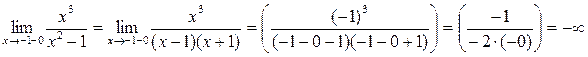
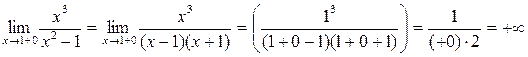
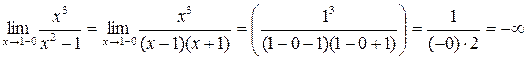
Поэтому прямые x = -1 и x = 1 являются вертикальными асимптотами.

3) Вычислим предел:

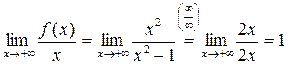, k = 1.

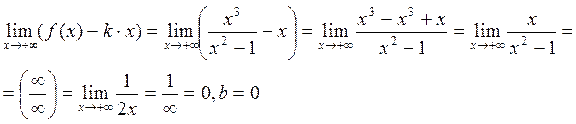
Отсюда следует, что при x ®+¥ прямая y = 1× x +0, т.е. y = x - наклонная асимптота при x®+¥.

Найдем наклонную асимптоту при x ®-¥.

Вычисляя те же пределы при x ®-¥, получим k = 1 и b = 0, то есть прямая y = x является наклонной асимптотой при x® -¥.

Ответ: x = ± 1 – вертикальные асимптоты

y = x – наклонная асимптота при x ® ±¥.