Непрерывность функции в точке и на промежутке

Определение 1. Функция f (x) называется непрерывной в точке x ₀Î D(f), если она определена в некоторой окрестности точки x₀ и предел f (x) в точке x₀ равен значению функции в этой точке, то есть:

= .

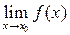Замечание. Из определения 1 следует правило вычисления предела функции в точке ее непрерывности:

= =

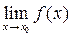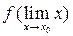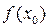
То есть предел функции в точке ее непрерывности равен значению функции в этой точке.

Определение 2. Функция f (x) называется непрерывной в точке x ₀Î D(f), если она определена в некоторой окрестности этой точки и бесконечно малому приращению аргумента 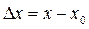соответствует бесконечно малое приращение функции , то есть: .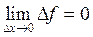

Определение 3. Функция f (x) называется непрерывной в точке x ₀Î D(f), если она определена в некоторой окрестности этой точки и существует правый и левый предел f (x) в точке 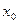, причем они равны междусобой и равны значению функции в этой точке, то есть:

а) 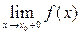= А;

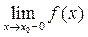б) = В;

в) А = В = .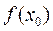

Определение 4. Функция f (x) называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка.