
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вычеты функций относительно особых точек.
|
|
Вычет в «бесконечности»
Для возможности более полного изучения свойств функции вводится понятие вычета в бесконечности, при этом она рассматривается как функция на сфере Римана(сфера Римана- система отсчета, заданная на сфере). Пусть бесконечно удалённая точка является изолированной особой точкой  , тогда вычетом в бесконечности называется комплексное число, равное
, тогда вычетом в бесконечности называется комплексное число, равное
 .
.
Цикл интегрирования в этом определении ориентирован положительно, то есть против часовой стрелки.
Аналогично предыдущему случаю вычет в бесконечности имеет представление и в виде коэффициента лорановского разложения в окрестности бесконечно удалённой точки:
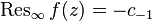 .
.
Вычет дифференциальной формы
С точки зрения анализа на многообразиях вводить специальное определение для некоторой выделенной точки сферы Римана (в данном случае, бесконечно удалённой) неестественно. Более того, такой подход затруднительно обобщить на более высокие размерности. Поэтому понятие вычета вводится не для функций, а для дифференциальных 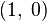 -форм на сфере Римана:
-форм на сфере Римана:
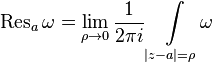 .
.
На первый взгляд разницы в определениях никакой, однако теперь 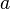 — произвольная точка
— произвольная точка 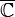 , и смена знака при вычислении вычета в бесконечности достигается за счёт замены переменных в интеграле.
, и смена знака при вычислении вычета в бесконечности достигается за счёт замены переменных в интеграле.
Логарифмические вычеты
Интеграл 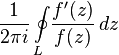 называется логарифмическим вычетом функции
называется логарифмическим вычетом функции  относительно контура
относительно контура 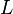 .
.