Правила приближенных вычислений

1. Сложение и вычитание. При сложении (и вычитании) приближен­ных чисел в окончательном результате следует сохранять столько де­сятичных знаков, сколько их в числе с наименьшим числом десятичных знаков, то есть в самом грубом слагаемом.

Например: 4.463 + 12, 38 + 1, 17273 + 121, 0262

Самое грубое слагаемое - второе имеет только два знака после запятой. Округлим остальные слагаемые до третьего знака после запя­той. Получим:

4, 463 + 12, 38 + 1, 173 + 121, 026 ≈ 139, 042 = 139, 04

В окончательном результате оставили только два знака после запятой.

Примечание: Если при округлении отбрасываемая часть состоит из одной цифры 5, то число округляют так, чтобы пос­ледняя цифра оставалась четной. Например, 12, 65 ≈ 12, 6; 9, 75 ≈ 9, 8.

2. Умножение и деление. При умножении (и делении) следует ок­руглять сомножители так, чтобы каждый из них содержал столько зна­чащих цифр, сколько их имеет сомножитель с наименьшим числом знача­щих цифр.

В промежуточных вычислениях оставляют на одну значащую цифру больше. В окончательном результате эта " запасная цифра" отбрасыва­ется. Например,

1, 2 ∙ 37, 82 ∙ 27380 ≈ 1, 2 ∙ 37, 8 ∙ 274 ∙ 100 = 1, 2∙ 10⁶,

43, 2/0, 63452 ≈ 43, 2/0, 6345 = 68, 1

Исключение: Можно сохранять еще одну цифру, если произведение начинается с единицы, а наименее точное число с какой-либо другой цифры. Например, 17, 63 ∙ 0, 88≈ 0, 88∙ 17, 6 =15, 5 (а не 15).

3. Возведение в степень (квадрат или куб). В результате следует сохранять столько значащих цифр, сколько их имеет возводимое в
степень приближенное число (последняя цифра квадрата и особенно куба при этом менее надежна, чем последняя цифра основания). Напри­мер, (1.32)² ≈ I, 74.

4. Извлечение квадратных и кубических корней. В результате
следует брать столько значащих цифр, сколько их имеет подкоренное
число. Последняя цифра квадратного и особенно кубического корня при этом более надежна, чем последняя цифра подкоренного.

5. Сложные выражения. В сложных вычислениях, если некоторые данные имеют больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в сте­пень, извлечении корня), чем другие, то их предварительно следует округлить, сохраняя только одну лишнюю цифру. Например,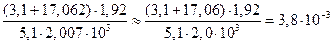

6. При решении задач по обработке лабораторных данных, необходимо пользоваться калькулятором с учетом всех перечисленных выше
правил.

При соблюдении этих правил можно считать, что в среднем полу­ченные результаты будут иметь все знаки верными, хотя в отдельных случаях возможна ошибка в 1- 2 единицы последнего знака.