
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Цифровой согласованный фильтр
|
|
В разделе рассматривалась основная особенность согласованного фильтра – то, что его импульсная характеристика представляет собой запаздывающую версию зеркального отображения (поворота относительно оси t = 0) входного сигнала. Таким образом, если сигнал равен s (t), его зеркальное отображение имеет вид s (-t), а зеркальное отображение, запаздывающее на Т секунд, имеет вид s (T-t). Следовательно, импульсная характеристика h (t), соответствующая сигналу s (t), будет равна следующему:
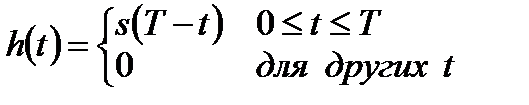 . (10.6)
. (10.6)
На рисунках 4.7 и 4.8 Л2 представлена основная функция коррелятора – интегрирование произведения принятого зашумленного сигнала с каждым опорным сигналом и определение наилучшего соответствия. Схемы, показанные на этих рисунках, подразумевают использование аналоговой аппаратуры (умножителей и интеграторов) и непрерывных сигналов. На них не отражена возможность реализации коррелятора или согласованного фильтра с использованием цифровых технологий и дискретных сигналов. Пример подобной реализации приведен на рисунке 4.10, где показан согласованный фильтр, использующий цифровую аппаратуру. Входной сигнал r (t) состоит из сигнала-прототипа si{t)и шума n (t); ширина полосы сигнала W =l/2T где Т – длительность передачи символа. Таким образом, минимальная частота дискретизации по Найквисту равна fs=2W= 1/ T, а время взятия выборки (Ts)должно быть не больше времени передачи символа. Другими словами, на символ должно приходиться не менее одной выборки. В реальных системах подобная дискретизация производится с частотой, в 4 или более раз превышающей минимальную частоту Найквиста. Платой за это является не увеличение полосы передачи, а увеличение быстродействия процессора. В моменты t = kTs выборки (как показано на рисунке 4.10, а)сдвигаются в регистре, так что более ранние из них располагаются правее. При дискретизации (взятии выборки) полученного сигнала непрерывное время t заменяется дискретным кТs, или просто к, что дает право использовать дискретную запись:
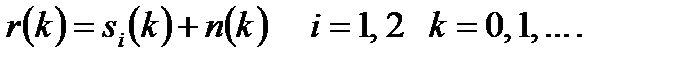
где i – индекс определяющий символ из M -арного набора (в нашем случае – двоичного);
к – дискретное время.
На рисунке 10.10 согласованный фильтр аппроксимируется регистром сдвига с весовыми коэффициентами сi (n), где п = 0,..., N – 1 – временной индекс весовых коэффициентов и разрядов регистра. В приведенном примере число разрядов регистра и количество выборок на символ равны 4. Итак, суммирование, показанное на рисунке, происходит в моменты времени от n = 0 до n = 3. Из расположения сумматора на схеме понятно, что решение относительно значения принятого сигнала принимается после заполнения регистра 4 выборками. Отметим, что для простоты в примере на рисунке 10.10, б выборки si (k)могут принимать только три значения (0, ±1). В реальных системах каждая выборка (и весовой коэффициент) – это 6-10 бит. Множеству весовых коэффициентов фильтра { сi (п)}соответствует импульсная характеристика фильтра; согласование весовых коэффициентов с выборками сигнала производится согласно дискретному варианту уравнения (4.26):
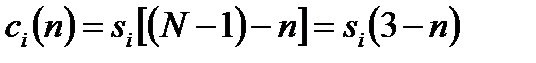 . (10.7)
. (10.7)
Использование дискретной формы интеграла свертки из уравнения (А.44, б) позволяет записать выражение с выхода коррелятора в момент времени, соответствующий k -й выборке:
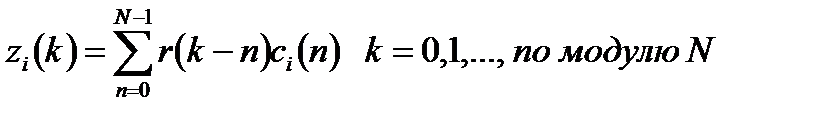 . (10.8)
. (10.8)
а) дискретный согласованный фильтр
б) пример детектирования с использованием дискретного
Рисунок 10.10 – Цифровой согласованный фильтр
Здесь х по модулю у – это остаток деления х на у, индекс к соответствует времени принятия выборок и выхода фильтра, а n фиктивная переменная времени. В формуле (4.28) выражение r(k – n) содержит и, которое можно рассматривать как «возраст» выборки (как давно она находится в фильтре). В выражении сi(n) n удобно рассматривать как адрес весового коэффициента. Предполагается, что система синхронизирована и упорядочение символов во времени известно. Также предполагается, что шум имеет нулевое среднее, так что математическое ожидание принятой выборки равно следующему:
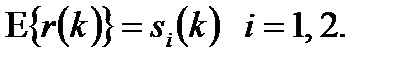
Следовательно, при передаче si(t) математическое ожидание выхода согласованного фильтра равно следующему:
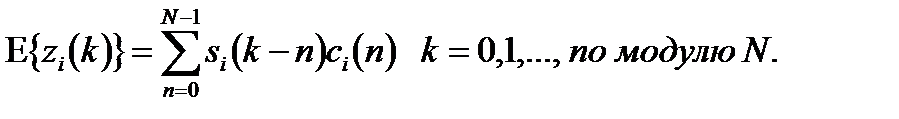 (10.9)
(10.9)
На рисунке 10.10, б, где сигналы-прототипы изображены как функции времени, видим, что крайняя слева выборка (амплитуда, равная +1) графика s1(t) представляет выборку в момент времени k = 0. Предполагая, что получен был сигнал s1(t) и для упрощения записи мы пренебрегли шумом, можем записать принятую выборку r(k) как s1(k). Выборки заполняют разряды согласованного фильтра, и в конце каждого периода передачи символа в крайнем правом разряде каждого регистра расположена выборка k = 0. Отметим, что в формулах (4.28) и (4.29) временные индексы и эталонных весовых коэффициентов расположены в порядке, обратном к временному индексу k – п выборок, что является ключевой особенностью интеграла свертки. То, что наиболее ранняя выборка теперь соответствует крайнему справа весовому коэффициенту, обеспечивает значащую корреляцию. Даже если действия согласованного фильтра мы математически опишем как свертку сигнала с импульсной характеристикой фильтра, конечный результат будет корреляцией сигнала с копией самого себя. По этой причине коррелятор можно реализовать как согласованный фильтр.
На рисунке 10.10, б детектирование, происходящее после выхода сигнала с согласованного фильтра, осуществляется обычным образом. Для принятия двоичного решения выходы zi(k) проверяются при каждом значении k= N-1, соответствующем концу символа. При условии передачи s1(t) и пренебрежении шумом, уравнения (4.27)-(4.29) можно объединить и записать выходы коррелятора в моменты времени k = N – 1 =3:
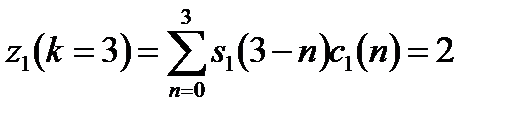 (10.3, a)
(10.3, a)
и
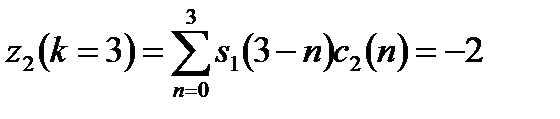 . (10.3, б)
. (10.3, б)
Поскольку z1(k = 3) больше z2(k = 3), детектор принимает решение, что передан был символ s1(t).
Может возникнуть вопрос: чем согласованный фильтр на рисунке.10, б отличается от коррелятора на рисунке 4.8. В случае согласованного фильтра в ответ на каждую новую выборку на входе появляется новое значение на выходе; следовательно, выход представляет собой временной ряд, такой как на рисунке 10.7, б (последовательность возрастающих положительных и отрицательных корреляций с входной синусоидой). Подобную последовательность на выходе согласованного фильтра можно получить при использовании нескольких корреляторов, работающих на разных начальных точках входного временного ряда. Отметим, что за время передачи символа на выходе коррелятора получаем максимальное значение сигнала в момент времени Т (рисунок 3.7, б). Если синхронизировать согласованный фильтр и коррелятор.
Некогерентное детектирование сигналов FSK
Детектор, выполняющий некогерентное детектирование FSK-модулированных сигаалов, описываемых уравнением (4.8), можно реализовать с помощью корреляторов, подобных показанным на рисунке 9.7. При этом оборудование приема следует настроить как детектор энергии без измерения фазы. По этой причине некогерентный детектор обычно требует вдвое большего числа ветвей-каналов, чем когерентный. На рисунке 9.18 показаны синфазный (I) и квадратурный (Q) каналы, используемые для некогерентного детектирования набора сигналов в бинарной модуляции FSK (BFSK). Отметим, что две верхние ветви настроены на детектирование сигнала с частотой ω 1 для синфазной ветви опорный сигнал имеет вид 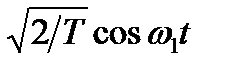 , а для квадратурной –
, а для квадратурной – 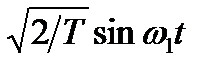 . Подобным образом две нижние ветви настроены на детектирование сигнала с частотой ω 2 для синфазной ветви опорный сигнал имеет вид
. Подобным образом две нижние ветви настроены на детектирование сигнала с частотой ω 2 для синфазной ветви опорный сигнал имеет вид 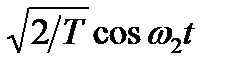 , а для квадратурной –
, а для квадратурной – 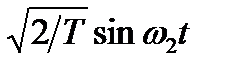 . Предположим, что принятый сигнал r(t) имеет вид точно
. Предположим, что принятый сигнал r(t) имеет вид точно 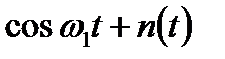 , т.е. фаза точно равна нулю. Следовательно, сигнальный компонент принятого сигнала точно соответствует (по частоте и фазе) опорному сигналу верхней ветви. В такой ситуации максимальный выход должен дать интегратор произведений верхней ветви. Вторая ветвь должна дать нулевой выход (проинтегрированный шум с нулевым средним), поскольку ее опорный сигнал
, т.е. фаза точно равна нулю. Следовательно, сигнальный компонент принятого сигнала точно соответствует (по частоте и фазе) опорному сигналу верхней ветви. В такой ситуации максимальный выход должен дать интегратор произведений верхней ветви. Вторая ветвь должна дать нулевой выход (проинтегрированный шум с нулевым средним), поскольку ее опорный сигнал  ортогонален сигнальному компоненту сигнала r(t). При ортогональной передаче сигналов (см. раздел 4.5.4Л.2) третья и четвертая ветви также должны дать близкие к нулю выходы порядка нуля, поскольку их опорные сигналы также ортогональны сигнальному компоненту сигнала r(t).
ортогонален сигнальному компоненту сигнала r(t). При ортогональной передаче сигналов (см. раздел 4.5.4Л.2) третья и четвертая ветви также должны дать близкие к нулю выходы порядка нуля, поскольку их опорные сигналы также ортогональны сигнальному компоненту сигнала r(t).
Рассмотрим теперь другую возможность. Пусть принятый сигнал r(t) имеет вид sin ω 1t + n(t). В этом случае максимальный выход должна дать вторая ветвь схемы (рисунок 10.18), а выходы других ветвей должны быть близки нулю. В реальной системе сигнал r(t) скорее всего описывается
Рисунок 10.18 – Квадратурный приемник
выражением 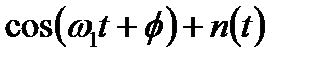 , т.е. входной сигнал будет частично коррелировать с опорным сигналом cos ω 1t и частично – с сигналом sin ω 1t. Поэтому некогерентный квадратурный приемник ортогональных сигналов и требует синфазной и квадратурной ветви для каждого возможного сигнала набора. Блоки, показанные на рисунке 4.18 после интеграторов произведений, выполняют операцию возведения в квадрат, что предотвращает появление возможных отрицательных значений. Затем для каждого класса сигналов набора (в бинарном случае – для двух) складываются величины
, т.е. входной сигнал будет частично коррелировать с опорным сигналом cos ω 1t и частично – с сигналом sin ω 1t. Поэтому некогерентный квадратурный приемник ортогональных сигналов и требует синфазной и квадратурной ветви для каждого возможного сигнала набора. Блоки, показанные на рисунке 4.18 после интеграторов произведений, выполняют операцию возведения в квадрат, что предотвращает появление возможных отрицательных значений. Затем для каждого класса сигналов набора (в бинарном случае – для двух) складываются величины 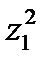 из синфазного канала и
из синфазного канала и 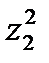 из квадратурного канала. На конечном этапе формируется тестовая статистика z(T) и выбирается сигнал с частотой ω 1, или ω 2, в зависимости от того, какая пара детекторов энергии дала максимальный выход.
из квадратурного канала. На конечном этапе формируется тестовая статистика z(T) и выбирается сигнал с частотой ω 1, или ω 2, в зависимости от того, какая пара детекторов энергии дала максимальный выход.
Существует еще одна возможная реализация некогерентного детектирования сигналов FSK. В этом случае используются полосовые фильтры, центрированные на частоте 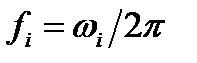 с полосой Wf= 1/T, за которыми, как показано на рисунке 4.19, следуют детекторы огибающей. Детектор огибающей состоит из выпрямителя и фильтра нижних частот. Детекторы согласовываются с огибающими сигнала, а не с самими сигналами. При определении огибающей фаза несущей не имеет значения. При бинарной FSK решение относительно значения переданного символа принимается путем определения, какой из двух детекторов огибающей дает большую амплитуду на момент измерения. Подобным образом для системы, использующей многочастотную фазовую манипуляцию (multiple frequency shift-keying – MFSK), решение относительно принадлежности переданного символа к одному из М возможных принимается путем определения, какой из М детекторов огибающей дает максимальный выход.
с полосой Wf= 1/T, за которыми, как показано на рисунке 4.19, следуют детекторы огибающей. Детектор огибающей состоит из выпрямителя и фильтра нижних частот. Детекторы согласовываются с огибающими сигнала, а не с самими сигналами. При определении огибающей фаза несущей не имеет значения. При бинарной FSK решение относительно значения переданного символа принимается путем определения, какой из двух детекторов огибающей дает большую амплитуду на момент измерения. Подобным образом для системы, использующей многочастотную фазовую манипуляцию (multiple frequency shift-keying – MFSK), решение относительно принадлежности переданного символа к одному из М возможных принимается путем определения, какой из М детекторов огибающей дает максимальный выход.
Рисунок 10.19 – Некогерентное детектирование сигналов FSK
с использованием детекторов огибающей
Детектор огибающей, изображенный на блочной диаграмме (рисунок 4.19), кажется проще квадратурного приемника, показанного на рисунке 4.18, но не стоит забывать, что.использование (аналоговых) фильтров обычно приводит к большей массе и стоимости детекторов огибающей по сравнению с квадратурным приемником. Поскольку квадратурные приемники могут реализовываться цифровым образом, с появлением больших интегральных схем их использование в качестве некогерентных детекторов стало предпочтительнее. Детектор, показанный на рисунке 4.19, может реализовываться цифровым образом, использование аналоговых фильтров заменяется выполнением дискретных.
Основная литература 1[155: 174].
Дополнительная литература 3[78: 96].
Контрольные вопросы
1.Что означает цифровой согласованный фильтр?
2.Что такое когерентное детектирование?
3. Что такое некогерентное детектирование?
Лекция №11. (1 час.)