Расширенный код Голея

Одним из наиболее практичных блочных кодов является двоичный расширенный код Голея (extended Golay code) (24, 12), который образован путем прибавления битов чет­ности к совершенному коду (23, 12), известному как код Голея (Golay code). Эти до­полнительные биты повышают минимальное расстояние 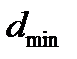с 7 до 8, что дает степень кодирования 1/2, реализовать которую проще (с точки зрения системного тактового генератора), чем степень кодирования кода Голея, равную 12/23. Расширенный код Голея значительно мощнее рассмотренного в предыдущем разделе кода Хэмминга. Цена, которую приходится платить за повышение эффективности, заключается в бо­лее сложном декодере и, соответственно, более широкой полосе пропускания.

Для расширенного кода Голея 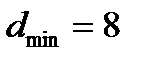, поэтому, исходя из уравнения (6.44), можно сказать, что код гарантирует исправление всех трехбитовых ошибок. Кроме того, де­кодер можно сконструировать так, чтобы он исправлял некоторые модели с четырьмя ошибками. Поскольку исправить можно только 16, 7% моделей с четырьмя ошибками, декодер, для упрощения, обычно реализуется для исправления только трехбитовых моделей ошибки [5]. Если предположить жесткое декодирование, то вероятность би­товой ошибки для расширенного кода Голея можно представить как функцию веро­ятности р ошибки в канальном символе (см. уравнение (6.46)):

(11.77)

График зависимости (11.77) показан на рис. 6.21; вероятность появления ошибки для рас­ширенного кода Голея значительно меньше, чем у кодов Хэмминга. Исходя из уравне