Известные блочные коды. Коды Хэмминга

Коды Хэмминга (Hamming codes) — это простой, класс блочных кодов, которые имеют следующую структуру:

(n, k ) = (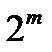 - 1, 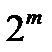- 1 - т), (13.1)

где m = 2, 3,.... Минимальное расстояние этих кодов равно 3, поэтому, согласно уравнениям (6.44) и (6.47), они способны исправлять все однобитовые ошибки или определять все модели ошибки из двух или малого числа ошибок в блоке. Декодиро­вание с помощью синдромов особенно хорошо подходит к кодам Хэмминга. Фактиче­ски синдром можно превратить в двоичный указатель местоположения ошибки [5]. Хотя Хэмминга не являются слишком мощными, они принадлежат к очень ог­раниченному классу блочных кодов, называемых совершенными; их особенности опи­сывались в разделе 6.5.4 коды. Если предположить, что используется жесткое декодирование, вероятность появ­ления битовой ошибки можно записать с помощью уравнения (6.46):

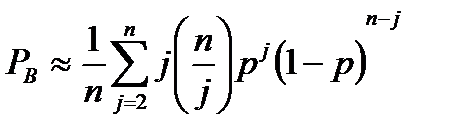(13.2)

Здесь р — вероятность ошибочного приема канального символа (вероятность перехода в двоичном симметричном канале). Для отдельных кодов коррекции ошибок (таких как ко­ды Хэмминга) вместо уравнения (6.72) мы можем использовать другое эквивалентное уравнение (это уравнение (Г. 16), которое выводится в приложении Г ):

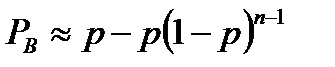(13.3)

На рис. 6.21 Л.2 приведен график зависимости вероятности ошибки в декодированном бите от вероятности ошибки в канальном символе, на котором сравниваются разные блочные коды. Для кодов Хэмминга на графике взяты значения m = 3, 4 и 5 или (п, к)- (7, 4), (15, 11), (31, 26). Для описания гауссового канала с использованием коге­рентной демодуляции сигналов BPSK, вероятность ошибки в канальном символе можно выразить через 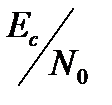, как это было сделано в уравнении (4.79Л2):

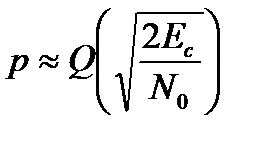(13.4)

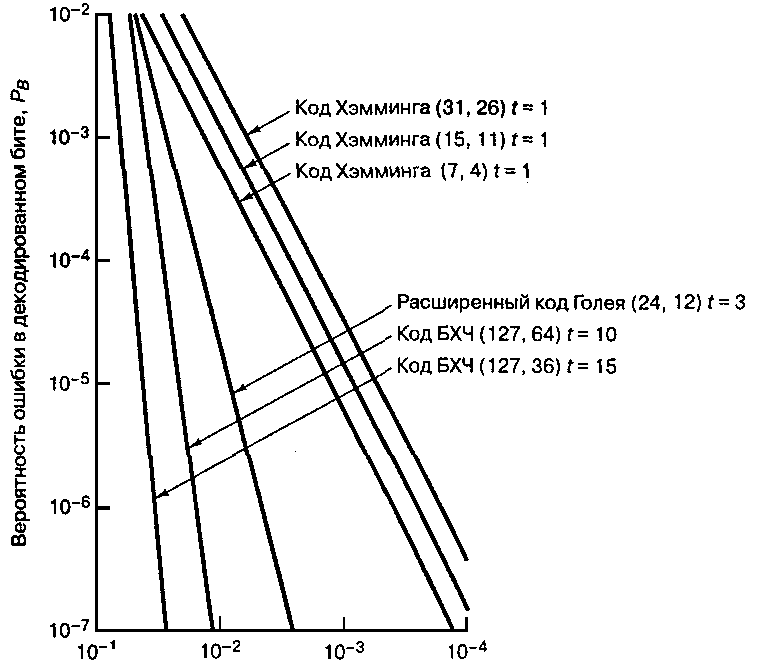
Вероятность ошибочного приёма канального символа, р

Рис. 11.21. Зависимость вероятности битовой ошибки от вероятности

ошибки в канальном символе для нескольких блочных кодов

. Здесь 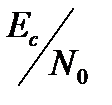— отношение энергии кодового символа к спектральной плотности мощ­ности шума, a Q(X) определено в уравнении (3.43). Чтобы связать 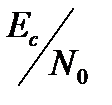с энергией би­та информации на единицу плотности спектрального шума (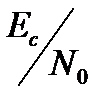), используем сле­дующее выражение:

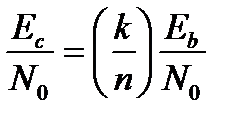. (11.5)

Для кодов Хэмминга уравнение (6.75) принимает следующий вид:

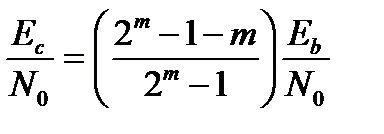. (11.6)

Объединяя уравнения (6.73), (6.74) и (6.76), 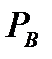при когерентной демодуляции сигна­лов BPSK в гауссовом канале можно выразить как функцию 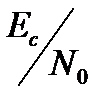. Результаты для различных типов блочных кодов отображены на рис. 11.22. Для кодов Хэмминга взяты следующие значения (п, к)= (7, 4), (15, 11), (31, 26).

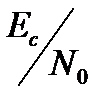(дБ)

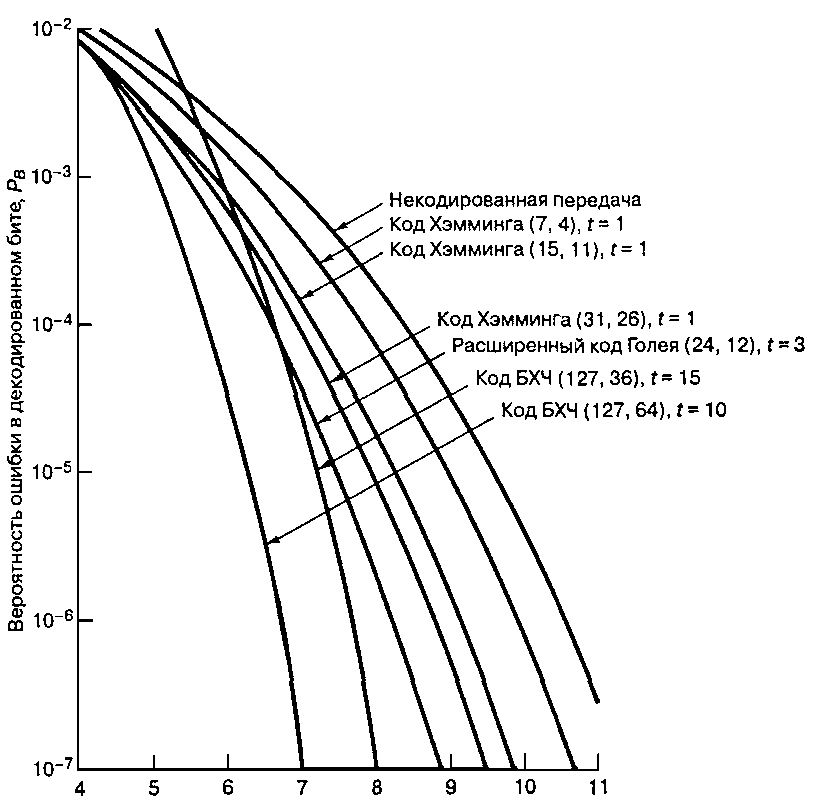
Рис. 11.22. Зависимость 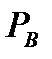от 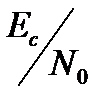при когерентной

демодуляции сигна­лов BPSK в гауссовом канале для

нескольких блочных кодов