Примеры решения задач. Пример 1. Определить число N молекул, содержащихся в объеме V=1 мм3 воды, и массу m1 молекулы воды

Пример 1. Определить число N молекул, содержащихся в объеме V =1 мм³ воды, и массу m ₁ молекулы воды. Считая условно, что молекулы воды имеют вид шариков, соприкасающихся друг с другом, найти диаметр d молекул.

Решение. Число n молекул, содержащихся в некоторой массе m, равно произведению числа Авогадро N_A на количество вещества n:

N = n N_A.

Так как количество вещества

n = m/m,

где m - молярная масса, то

.

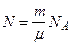Выразив в этой формуле массу как произведение плотности на объем V, получим

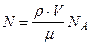(1)

Подставим в формулу (1) следующие значения величин: r =10³ кг/м³; V = 1 мм³=10^-9 м³; m =18× 10^-3 кг/моль; N_A =6, 02× 10²³ моль^-1 и произведем вычисления:

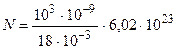молекул=3, 34× 10¹⁹ молекул.

Массу m₁ одной молекулы можно найти делением молярной массы на число Авогадро:

.

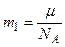Подставив сюда числовые значения m и N, найдем массу молекулы воды:

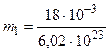кг = 2, 99× 10^-26 кг.

Если молекулы воды, плотно прилегают друг к другу, то можно считать, что на каждую молекулу приходится объем (кубическая ячейка) V₁=d³, где d - диаметр молекулы. Отсюда

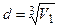. (2)

Объем V ₁ найдем, разделив молярный объем V_m на число молекул в моле, т.е. на число Авогадро N _A:

V₁ =V_m /N_A.

Подставим полученное выражение V ₁ в формулу (2):

.

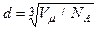Входящий в эту формулу молярный объем определяется выражением V_m =m / r. Тогда искомый диаметр молекулы

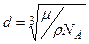(3)

Проверим, дает ли правая часть выражения (3) единицу длины:

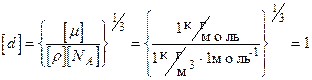м.

Теперь подставим числовые значения физических величин в формулу (3) и произведем вычисления:

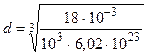м = 3, 11× 10^-10 м = 311 пм.

Пример 2. В баллоне объемом V = 10 л находится гелий под давлением р₁ =1 МПа и при температуре

Т ₁ = 300 К. После того как из баллона было взято

m =10 г гелия, температура в баллоне понизилась до Т ₂=290 К. Определить давление р ₂ гелия, оставшегося в баллоне.

Решение. Для решения задачи воспользуемся уравнением Менделеева-Клапейрона, применив его к конечному состоянию газа:

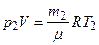, (1)

где m₂ -масса гелия в баллоне в конечном состоянии; m - молярная масса гелия; R - молярная газовая постоянная.

Из уравнения (1) выразим искомое давление р₂:

. (2)

Массу гелия m ₂ выразим через массу m ₁, соответствующую начальному состоянию, и массу m гелия, взятого из баллона:

m₂ = m₁ - m. (3)

Массу гелия m ₁ найдем также из уравнения Менделеева-Клапейрона, применив его к начальному состоянию:

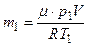. (4)

Подставляя в выражение (3) массу m ₁ из формулы (4), а затем полученное выражение m ₂ в формулу (2), найдем

,

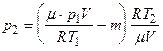или после преобразования и сокращения

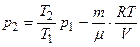. (5)

Пример 3. Баллон содержит m ₁=80 кг кислорода и m ₂=320 г аргона. Давление смеси p =1 МПа, температура Т =300 К. Принимая данные газа за идеальные, определить объем V баллона.

Решение. По закону Дальтона, давление смеси равно сумме парциальных давлений газов, входящих в состав смеси. Парциальным давлением газа называется давление, которое производил бы этот газ, если бы только он один находился в сосуде, занятом смесью.

По уравнению Менделеева-Клапейрона, парциальные давления кислорода p ₁ и аргона р ₂ выражаются формулами:

; .

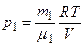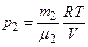Следовательно, по закону Дальтона давление смеси газов

р = р ₁+ р ₂, или ,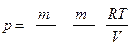

откуда объем баллона

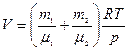(1)

Выразим в единицах СИ числовые значения величин, входящих в формулу: m ₁=80 г=0, 08 кг, m₁=32× × 10^-3 кг/моль, m ₂=320 г=0, 32 кг, m₂=40× 10^-3 кг/моль, р =1 МПа=10⁶ Па, R =8, 31 Дж/(моль× К).

Подставим числовые значения в формулу (1) и произведем вычисления:

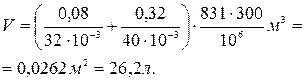
Пример 4. Вычислить удельные теплоемкости с_v и c_p смеси неона и водорода, если массовая доля неона w ₂=20 %. Значения удельных теплоемкостей газов взять из предыдущего примера.

Решение. Удельную теплоемкость смеси при постоянном объеме c_v найдем следующим образом. Теплоту, необходимую для нагревания смеси на D Т, выразим двумя способами:

Q=c_V (m ₁ +m ₂)D T, (1)

Q= (c_{V, 1} m ₁ +c_{V, 2} m ₂)D T, (2)

где с_{V, 1} - удельная теплоемкость неона; с_{V, 2} - удельная теплоемкость водорода.

Приравняв правые части (1) и (2) и разделив обе части полученного равенства на D Т, получим

с_V (m ₁ +m ₂)= c_{V, 1} m ₁ +c_{V, 2} m ₂,

откуда

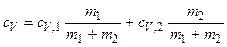, (3)

или

с_V = c_{V, 1} w ₁ +c_{V, 2} m ₂, (4)

где 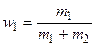и 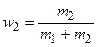- массовые доли неона и водорода в смеси.

Подставив в формулу (4) числовые значения величин, найдем:

с_V = (6, 24× 10²× 0, 8+1, 04× 10⁴× 0, 2) Дж/(кг× К) =

= 2, 58× 10³ Дж/(кг× К).

Рассуждая таким же образом, получим формулу для вычисления удельной теплоемкости смеси при постоянном давлении:

с_р = с_{р, 1} w ₁ + c _{p , 2} w ₂. (5)

Подставим в формулу (5) числовые значения величин:

с_р= 1, 04× 10³× 0, 8+1, 46× 10⁴× 0, 2 Дж/(кг× К)=3, 75× 10³ Дж/(кг× К).

Пример 5. Кислород массой m =2 кг занимает объем V ₁=1 м³ и находится под давлением р ₁=0, 2 МПа. Газ был нагрет сначала при постоянном давлении до объема V ₂=3 м³, а затем при постоянном объеме до давления р ₃=0, 5 МПа. Найти изменение D U внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.

Решение. Изменение внутренней энергии газа выражается формулой

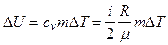(1)

где i -число степеней свободы молекул газа (для двухатомных молекул кислорода i =5); m-молярная масса.

Начальную и конечную температуру газа найдем из уравнения Клапейрона-Менделеева :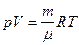

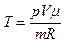. (2)

Выпишем заданные величины в единицах СИ: m= 2 кг, m=32× 10^-3 кг/моль, R =8, 31 Дж/(моль× К), V ₁=1 м³, V ₂= V ₃=3 м³, р ₁= р ₂=0, 2 МПа=2× 10⁵ Па, р ₃=0, 5 Мпа =

=5× 10⁵ Па. Подставляя эти значения в выражение (2) и выполняя арифметические действия, получим:

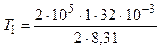К = 385 К;

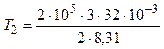К = 1155 К = 1, 16 кК;

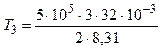К = 2887 К = 2, 89 кК.

Подставляя в выражение (1) числовые значения величин, входящих в него, и выполняя арифметические действия, находим

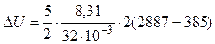Дж= 3, 24× 10⁶ Дж =3, 24 МДж

Работа расширения газа при постоянном давлении выражается формулой .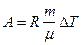

Подставив числовые значения величин, получим

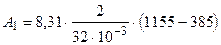Дж = 0, 400× 10⁶ Дж.

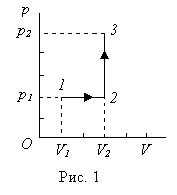
Работа газа, нагреваемого при постоянном объеме, равна нулю, т.е. А ₂=0. Следовательно, полная работа, совершенная газом, равна

А=А ₁+ А ₂=0, 4× 10⁶ Дж.

Согласно первому началу термодинамики, теплота Q, переданная газу, равна сумме изменения внутренней энергии D U и работы А: Q = D U+A, следовательно,

Q =0, 4× 10⁶ Дж+3, 24× 10⁶ Дж=3, 64× 10⁶ Дж=3, 64 МДж.

График процесса приведен на рис.1.

Пример 6. В цилиндре под поршнем находится водород массой m =0, 02 кг при температуре T =300 К. Водород сначала расширился адиабатически, увеличив свой объем в n ₁=5 раз, а затем был сжат изотермически, причем объем газа уменьшился в n ₂=5 раз. Найти температуру в конце адиабатического расширения и работу, совершенную газом при этих процессах. Изобразить процесс графически.

Решение. Температуры и объемы газа, совершающего адиабатический процесс, связаны между собой соотношением

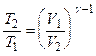, или ,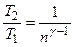

где g-отношение теплоемкости газа при постоянном давлении и постоянном объеме (для водорода как двухатомного газа g=1, 4):

n ₁ = V ₂/ V ₁ = 5.

Отсюда получаем следующее выражение для конечной температуры Т ₂:

.

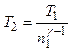Подставляя числовые значения заданных величин, находим

.

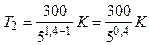Так как 5^{0, 4}=1, 91 (находится логарифмированием), то

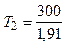К= 157 К.

Работа А ₁ газа при адиабатическом расширении может быть определена по формуле

,

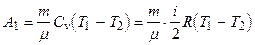где C_v - молярная теплоемкость газа при постоянном объеме.

Подставив числовые значения величин: R =8, 31 Дж/(моль× К), i =5 (для водорода как двухатомного газа), m=2× 10^-3 кг/моль, m =0, 02 кг, Т ₁=300 К, Т ₂=157 К в правую часть последней формулы и выполняя арифметические действия, получим

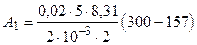Дж=2, 98× 10⁴ Дж.

Работа А ₂ газа при изотермическом процессе может быть выражена в виде

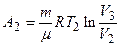, или ,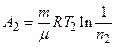

где n ₂= V ₂/ V ₃=5.

Подставляя известные числовые значения величин, входящих в правую часть этого равенства, и выполняя арифметические действия, находим

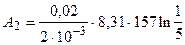Дж= = -2, 10× 10⁴ Дж.

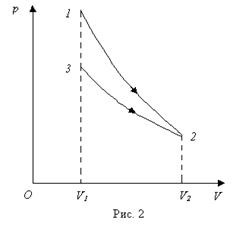
Знак “минус” показывает, что работа совершается над газом внешними силами. График процесса приведен на рис.2

Пример 7. Тепловая машина работает по обратимому циклу Карно. Температура нагревателя Т ₁=500 К. Определить термический к.п.д. h цикла и температуру Т ₂ охладителя тепловой машины, если за счет каждого килоджоуля теплоты, полученной от нагревателя, машина совершает работу А =350 Дж.

Решение. Термический к.п.д. тепловой машины, называемый также коэффициентом использования теплоты, показывает, какая доля теплоты, полученной от нагревателя, превращается в механическую работу. Термический к.п.д. выражается формулой

,

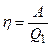где Q ₁ - теплота, полученная от нагревателя; А - работа, совершенная рабочим телом тепловой машины.

Подставив числовые значения в эту формулу, получим

.

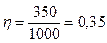Зная к.п.д. цикла, можно по формуле 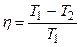определить температуру охладителя Т₂:

Т ₂= Т ₁(1- h).

Подставив в эту формулу полученное значение к.п.д. и температуры Т ₁ нагревателя, получим

Т ₂=500(1-0, 35) К=325 К.

Пример 8. В сосуде объемом V =30 л находится m =100 г кислорода под давлением р =3× 10⁵ Па. Определить наиболее вероятное значение кинетической энергии молекул О₂.

Решение. Вероятное значение кинетической энергии молекул соответствует максимум кривой распределения Максвелла по кинетическим энергиям

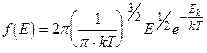(1)

Задача сводится к нахождению экстремума функции f (E).

Определим первую производную g ’(E) и приравняем ее нулю, получим

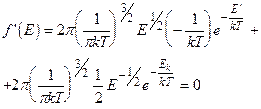(2)

Отсюда Е _в =kT/2 (3) температуру найдем из уравнения Менделеева-Клайперона

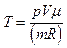(4)

Подставим (4) в (3) и получим

=16× 10^-22Дж=

=1, 6× 10^-21 Дж.

Пример 9. Определить массу воздуха в цилиндре с основанием D S =1 м² и высотой h =1 км. Считать, что воздух находится при нормальных условиях.

Решение. Распределение Больцмана для одномерного случая имеет вид

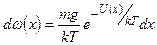
Число молекул dN в слое воздуха толщиной dx на высоте х от поверхности Земли

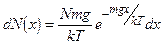
Проинтегрировав dN (x) по х в пределах от 0 до h, найдем полное число молекул в данном цилиндре

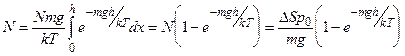
Умножив N на массу одной молекулы, получим искомую массу

,
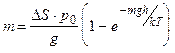