Дифференциальные уравнения движения невязкой жидкости

ОСНОВНЫЕ УРАВНЕНИЯ ГИДРОДИНАМИКИ

Дифференциальные уравнения движения невязкой жидкости

Выделим в потоке невязкой жидкости элементарный объем в форме параллелепипеда со сторонами dx, dy, dz (рис. 4.1). Второй закон Ньютона для массы жидкости в этом объеме в проекции на ось 0x

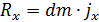, (4.1)

где R_x - проекция равнодействующей внешних сил; 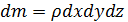- масса жидкости; j_x - проекция ускорения, определяемая формулой (3.9) из Лекции 4:

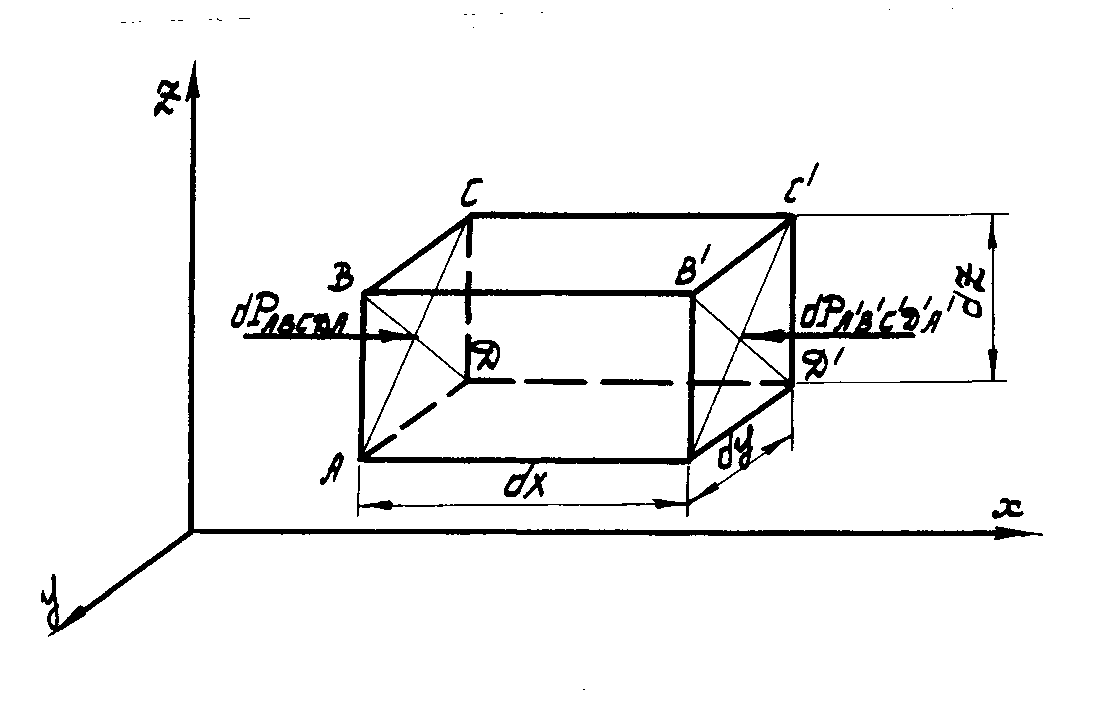Рис. 4.1

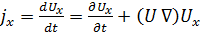Проекция силы давления на грань АВСД

dP_АВСД=p·dy·dz,

где p - среднее давление на грань.

Среднее давление на грань A'B'C'Д'

.

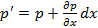Сила давления на эту грань

.

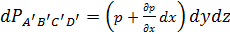Проекции на ось 0x сил давления на другие грани параллелепипеда равны нулю, поэтому сумма проекций сил давления на грани АВСД и A'B'C'Д'

.

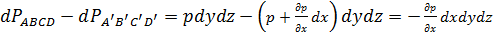Проекция объемных (массовых) сил на ось 0x 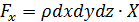, где X - проекция ускорения, вызванного массовыми силами, на ось 0x.

Подставляя выражения для проекций сил в (4.1), получим

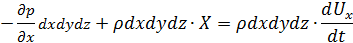
или, после деления на ,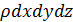

.

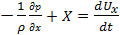Аналогичные уравнения можно написать и для других координатных осей.

В результате получим уравнения Эйлера для движения сплошной среды:

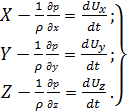(4.2)

Три уравнения (4.2) содержат четыре неизвестные функции U_x, U_y, U_z и p. Поэтому для решения системы необходимо еще одно уравнение, связывающее эти функции. Такое уравнение есть – это уравнение неразрывности (3.15) (или (3.17) для несжимаемой жидкости).

Уравнения Эйлера, учитывая формулы (3.9), записывают также в виде:

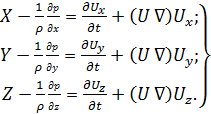(4.2а)