Гипотезы Буссинеска и Прандтля о турбулентных напряжениях

Рассмотрим прямолинейный установившийся турбулентный поток с неравномерным распределением усредненных скоростей (рис. 5.8).

Гипотеза Буссинеска, связывающая турбулентные напряжения τ _Т с усредненной скоростью :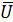

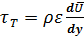, (5.39)

где ε - кинематический коэффициент турбулентной вязкости.

Рис. 5.8

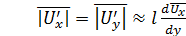. (5.40)

Следовательно,

.

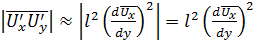Модуль касательного турбулентного напряжения (А), входящего в уравнения Рейнольдса, теперь выражается как

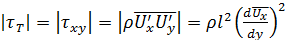. (5.41)

Коэффициент l в (5.40) и (5.41) называют длиной пути перемешивания. Для определения этого понятия допускается, что жидкая частица, имевшая в слое 1 усредненную скорость 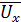(рис. 5.8), под влиянием турбулентной пульсации 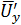перемещается на расстояние l в слой 2, где усредненная скорость равна 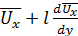. Основное допущение этой гипотезы заключается в том, что путь l между слоями 1 и 2 частица проходит без взаимодействия с другими частицами, т. е. так же, как молекула газа проходит путь свободного пробега. Тогда в результате смешения с частицами слоя 2 переместившаяся частица приобретает усредненную скорость этого слоя, т. е. в нем будет иметь место пульсация продольной скорости.

Связь между кинематическим коэффициентом турбулентной вязкости ε и длиной l устанавливается из сопоставления (5.39) и (5.41):

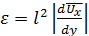. (5.42)

Гипотезы Буссинеска и Прандтля сводят задачу отыскания связи турбулентных касательных напряжений с усредненными скоростями к задаче определения функций координат ε и l.

Задача определения функций ε и l решается с привлечением экспериментальных данных и дополнительных гипотез. Прандтль, в частности, предположил, что для полуограниченного турбулентного потока вблизи плоской стенки справедлива линейная связь длины l и расстояния y от стенки: l = ϰ y (где ϰ - универсальная постоянная).