
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Интегрирование уравнений Эйлера
|
|
Уравнения равновесия
Умножим уравнения (2.7) соответственно на dx, dy и dz и сложим:
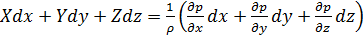 . (2.8)
. (2.8)
Выражение в скобках правой части (2.8) - полный дифференциал гидростатического давления dp, следовательно,
ρ (Xdx + Ydy + Zdz) = dp. (2.9)
Уравнение (2.9) - основное дифференциальное уравнение гидростатики.
Проинтегрируем (2.9) для случая, когда жидкость заключена в закрытый сосуд и покоится под действием силы тяжести и внешнего давления p 0 на свободную поверхность (рис. 2.3).
Горизонтальную плоскость X0Y назовём плоскостью сравнения. Проекции g на координатные оси Х =0, Y =0, Z=-g. Значит
 Рис. 2.3
Рис. 2.3
|
Интегрируем (2.10):
p=-ρ gz+C. (2.11)
При р=р 0 и z=z 0 C=p 0 + ρ gz 0.
Подставим это выражение в (2.11):
p = -ρ gz + р 0+ ρ gz 0, (2.12)
или
p = p 0 + ρ g (z 0 - z) = p 0 + ρ gh. (2.13)
Окончательно
p = p 0 + ρ gh. (2.14)
Разделив (2.12) на ρ g, получим:
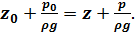 (2.15)
(2.15)
Уравнения (2.14) и (2.15) – два вида основного уравнения гидростатики в интегральной форме.