
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Синтез комбинационных схем на 8-канальных мультиплексорах
|
|
Пусть требуется реализовать функцию f1(v) (рис. 4.7, а) четырех переменных x4, x3, x2 и x1 на мультиплексоре 8 → 1. Такой мультиплексор имеет три адресных входа, на которые можно подать три из четырех переменных. Пусть на адресные входы мультиплексора с весами 4, 2, 1 подаются переменные x3, x2 и x1 соответственно. Тогда адрес входного канала мультиплексора Di, будет определяться числом i = e3 e2 e1 = 0, 1, …, 7. Напомним, что клетки диаграмм Вейча четырех переменных нумеруются числами j = e4 e3 e2 e1 = 0, 1...., 15 (рис. 4.7, в) на основании обозначения их сторон переменными  . Аналогично можно пронумеровать клетки диаграммы Вейча адресами каналов i мультиплексора, не учитывая переменную
. Аналогично можно пронумеровать клетки диаграммы Вейча адресами каналов i мультиплексора, не учитывая переменную 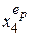 (рис. 4.7, г).
(рис. 4.7, г).

Рис. 4.7 Диаграммы Вейча для функций f1(v), f2(v)
Как видно из (рис. 4.7, г) числа i произвели разбиение диаграммы Вейча на восемь частей, каждая из которых представляет собой диаграмму Вейча для одной переменной x 4. Эти восемь диаграмм Вейча одной переменной х 4 определяют функции 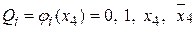 , которые следует подать на информационные входы мультиплексора Qi. Из рис. 4.7, а и рис. 4.7, г следует, что
, которые следует подать на информационные входы мультиплексора Qi. Из рис. 4.7, а и рис. 4.7, г следует, что
D 0 =  , D 1 = 1, D 2 = 0, D 3 = 0,
, D 1 = 1, D 2 = 0, D 3 = 0,
D 4 =  , D 5 = x 4, D 6 = x 4, D 7 = 0.
, D 5 = x 4, D 6 = x 4, D 7 = 0.
Проверка результата синтеза:

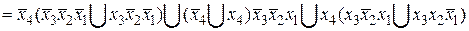 ,
,
что совпадает с функцией, представленной на (рис. 4.7, а).
По полученным значениям Di, можно реализовать функцию f 1 (v) на мультиплексоре 8 → 1 (рис. 4.8).
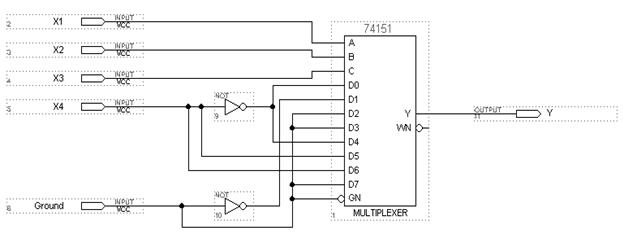
Рис. 4.8 Реализация функции f1(v) на мультиплексоре 8 à 1 (SN74ALS151)
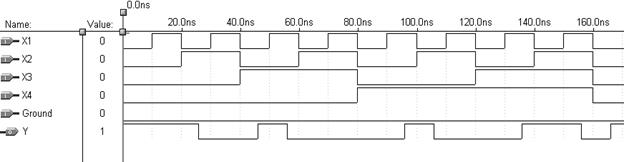
Рис. 4.9 Временные диаграммы для реализации функции f1(v) на мультиплексоре 8 à 1 (SN74ALS151)
При выборе иных переменных в качестве адресных получится другая схема. Предпочтение следует отдать той схеме, на информационные входы которой подается большее число констант 0 и 1. Оптимальную с этой точки зрения схему можно получить, выполнив синтез для всех возможных вариантов комбинаций адресных сигналов, разбиения диаграмм Вейча для которых показаны на (рис. 4.10).
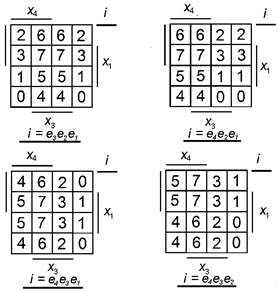
Рис. 4.10 Диаграммы Вейча для функций f1(v), f2(v)
Таблица 4.4
Значения Di, для различных комбинаций адресных сигналов
| Вход | I | |||
| e3 e2 e1 | e4 e2 e1 | e4 e3 e1 | e4 e3 e2 | |
| D0 | 
| 
| ||
| D1 | 
| 
| ||
| D2 | 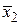
| 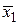
| ||
| D3 | ||||
| D4 | 
| X1 | ||
| D5 | x4 | 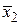
| ||
| D6 | x4 | x3 | x2 | X1 |
| D7 | 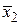
| 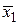
|
В (табл. 4.4) указаны значения Di, для различных комбинаций адресных сигналов. Наилучший вариант схемы получается при задании адресов числами i = e 4 e 2 e 1; все значения Di, заменены на инверсные 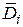 , так как выход мультиплексора 155КП5 инверсный).
, так как выход мультиплексора 155КП5 инверсный).
Из рис. 4.7а следует, что МДНФ функции

Так как внутренний дешифратор мультиплексора 8→ 1 реализует восемь минтермов трех переменных, то в качестве адресных сигналов следует использовать те переменные, которые входят в МДНФ наибольшее число раз. В этом случае внутренний дешифратор мультиплексора будет нести наибольшую логическую нагрузку. Такой подход к выбору адресных сигналов позволяет исключить полный перебор всех вариантов. Из полученной МДНФ видно, что наименьшее число раз в нее входит первичный терм  , поэтому в качестве адресных сигналов предпочтительнее использовать переменные x 4, x 2 и x 1.
, поэтому в качестве адресных сигналов предпочтительнее использовать переменные x 4, x 2 и x 1.
Из (рис. 4.7, б) следует, что МДНФ функции
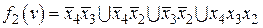 .
.
Из формулы видно, что функция f 2(v) является вырожденной (не зависит от переменной x 1). Задав адреса числами i = e 4 e 3 e 2, на основании (рис. 4.3, б) можно получить:
D 0 = 1, D 1 = 1, D 2 = 1, D 3 = 0,
D 4 = 1, D 5 = 0, D 6 = 0, D 7 = 1.
По полученным значениям Di, можно реализовать функцию f2(v) на мультиплексоре 8 → 1 (рис. 4.11).
 Рис. 4.11 Реализация функции f2(v) на мультиплексоре 8 à 1 (SN74ALS151)
Рис. 4.11 Реализация функции f2(v) на мультиплексоре 8 à 1 (SN74ALS151)

Рис. 4.12 Временные диаграммы для реализации функции f2(v) на мультиплексоре 8 à 1 (SN74ALS151)
4.6 Синтез на двухразрядных 4-канальных мультиплексорах
Двухразрядные мультиплексоры 4→ 1 достаточно просто использовать для реализации двух функций трех и четырех переменных. Пусть функции f 1(v) и f 2(v) заданы диаграммами Вейча (рис. 4.7, а, б). Мультиплексор 4→ 1 имеет два адресных входа, а значит, возможны шесть вариантов выбора переменных для адресных сигналов: x 2и x 1, x 3и x 1, x 4и x 1, x 3и x 2, x 4 и x 2, x 4и x 3. Соответствующие числа i = ep eq (p ≠ q) будут определять адреса каналов мультиплексора. Так как числа i двухразрядные, то они будут разбивать диаграмму Вейча четырех переменных на четыре части, каждая из которых представляет собой диаграмму Вейча для двух переменных, не использованных в качестве адресных. На (рис. 4.15) показаны все шесть вариантов разбиения диаграмм Вейча адресами i. Так как адресные сигналы у двухразрядного мультиплексора 4→ 1 общие для обоих разрядов, то можно проводить только совместную минимизацию функций f1(v) и f2(v).
Для оптимального выбора адресных переменных следует подсчитать общее число первичных термов  , входящих в обе МДНФ, и в качестве адресных переменных выбрать те, первичные термы которых входят наибольшее число раз в эти МДНФ. В данном примере такими переменными являются x 4 и x 2. Тогда на основании (рис. 4.7, а, б) и (рис. 4.15) можно получить:
, входящих в обе МДНФ, и в качестве адресных переменных выбрать те, первичные термы которых входят наибольшее число раз в эти МДНФ. В данном примере такими переменными являются x 4 и x 2. Тогда на основании (рис. 4.7, а, б) и (рис. 4.15) можно получить:
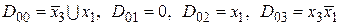 - для f 1(v);
- для f 1(v);
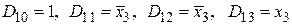 – для f 2(v).
– для f 2(v).
Этим значениям информационных входов соответствует схема, изображенная на рис. 4.13.

Рис. 4.13 Реализация функций f1(v) и f2(v) на мультиплексоре SN74ALS153
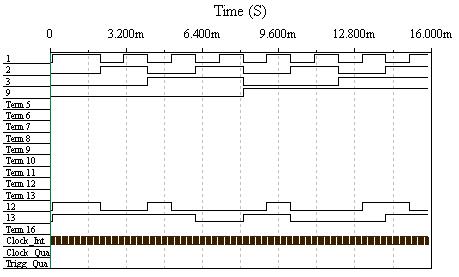
Рис. 4.14 Временные диаграммы для реализация функций f1(v) и f2(v)
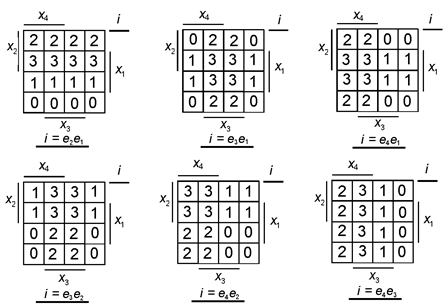
Рис. 4.15 Варианты разбиения диаграмм Вейча адресами i
Как известно, МДНФ и МКНФ могут значительно различаться по число входящих в них первичных термов, поэтому для оптимального выбора адресных переменных следует использовать также подсчет вхождений первичных термов  в МКНФ (или в МДНФ инверсной функции). Изложенный метод выбора адресных переменных можно использовать в качестве инженерного метода синтеза КС на мультиплексорах для исключения перебора всех возможных вариантов.
в МКНФ (или в МДНФ инверсной функции). Изложенный метод выбора адресных переменных можно использовать в качестве инженерного метода синтеза КС на мультиплексорах для исключения перебора всех возможных вариантов.