Следовательно, действие силы на твердое тело не изменяется при переносе ее параллельно самой себе в другую точку твердого тела, если добавить пару сил.

Произвольную систему сил, приложенную к твердому телу, можно заменить одной силой — главным вектором и одной парой сил — главным моментом, не нарушая при этом со­стояние твердого тела.

~ .

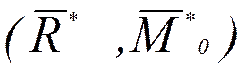Условия и уравнения равновесия произвольной пространственной системы сил

Для равновесия произвольной пространственной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор и главный момент этой системы сил равнялись нулю.

Условия равновесия в векторной форме:

.

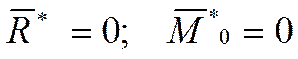Уравнения равновесия:

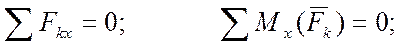
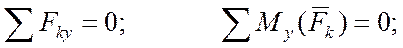
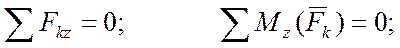
Задача 1. Дверь ABDE весом G =240 Н удерживается открытой на угол FBD = 120^о двумя веревками. К веревке DFK, перекинутой через блок F, подвешен груз весом Q =60 Н; веревка EL, протянутая перпендикулярно двери, закреплена в точке L пола. Размеры двери: АВ =2 м, АЕ =0, 8 м. Определить реакции подпятника А и подшипника В и натяжение веревки EL. (рисунок 1).

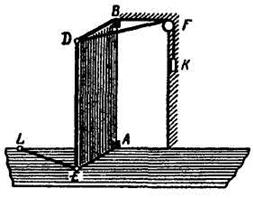
Рис.1

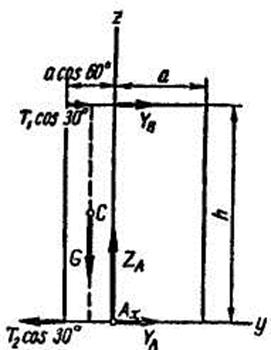
Рисунок 2.

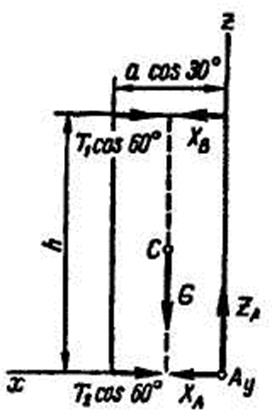
Рис.3

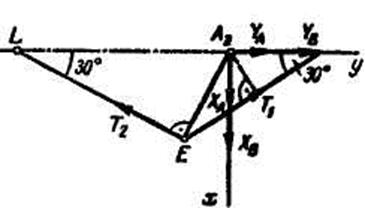
Рис.4

1.

,

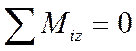
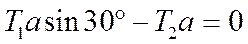откуда

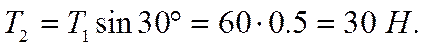
2.

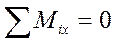
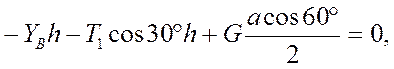
откуда

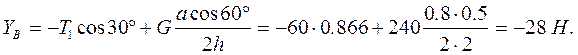
3.

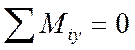
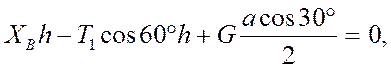
откуда

.

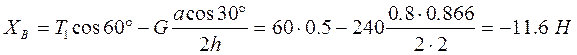Для определения проекций сил Х_А, У_А, Z_А, не вошедших в уравнение моментов, составляем три уравнения проекций.

4.

,

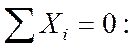
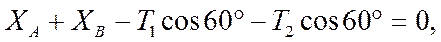откуда

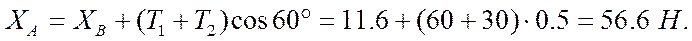
5.

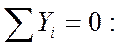
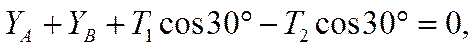
откуда

.

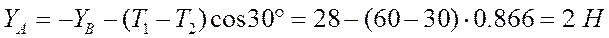6.

,

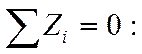
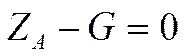откуда

.

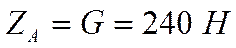Задача 2. На рисунке 1 изображен коленчатый вал двигателя. При вертикальном положении средней плоскости колена давление шатуна на середину шейки вала составляет Р = 12 кН и направлено в плоскости, перпендикулярной оси вала, под углом 15^о к горизонтали.

На оси вала в точке С закреплен маховик весом G =12 кН. В точке Е укреплен шкив диаметром D = 80 см с ремнем, передающим момент на вал рабочей машины. Ветви ремня лежат в плоскости шкива и составляют с горизонталью угол, равный 30°. Отношение натяжения ведущей и ведомой ветвей Т/t = 2.

Расстояние от оси шейки колена до оси вала r = 15 см. Расстояния по оси вала указаны на рисунке 1 в сантиметрах. Определить натяжения ветвей ремня T и t реакции подшипников A и B при равномерном вращении вала и при заданном его положении. (Весом шкива в вала можно пренебречь.)

Решение. При равномерном вращении правильно сконструированного привода приложенные к нему силы должны удовлетворять условиям их равновесия.

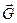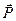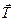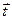Прикладываем к валу задаваемые силы: вес маховика , давление шатуна на шейку вала и реакции ветвей ремня и , направленные по касательной к окружности обода шкива. Отбрасывая связи (подшипника), прикладываем к валу их реакции, разложенные на составляющие 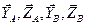(рисунок 1).

Выбрав оси координат, как показано на рисунке 2, составляем уравнения равновесия сил, произвольно расположенных в пространстве. Вал имеет две точки опоры А и В; первым составляем уравнение моментов относительно оси х, проходящей через эти точки. Пользуемся рисунком 3, так как на нем изображены только силы, моменты которых относительно оси х не равны нулю

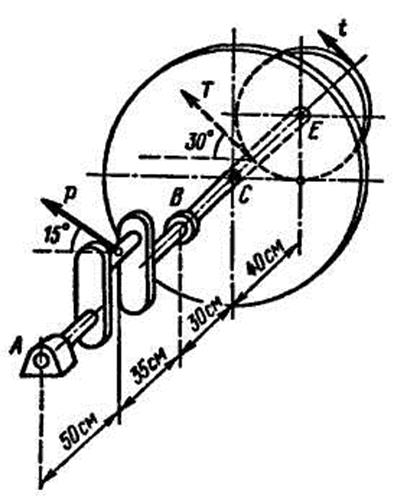
Рис.1

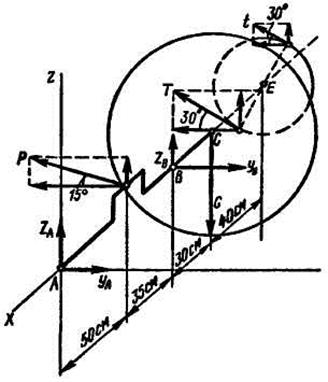
Рис. 2

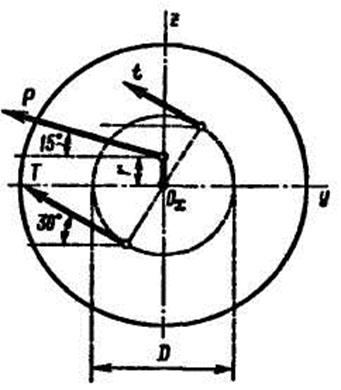
Рис.3

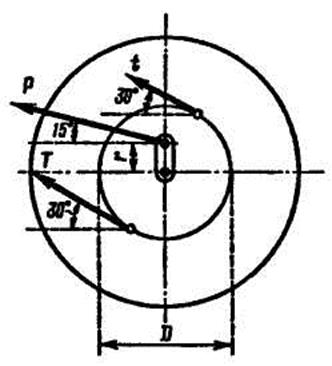
Рис.4

l. :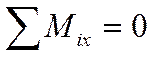

.

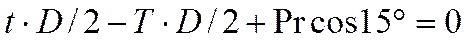Так как Т =2 t, то модули сил t и Т можно определить так:

,

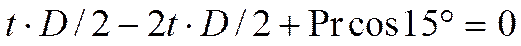откуда

.

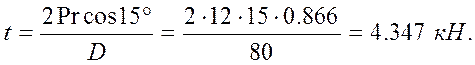Затем составляем следующие уравнения моментов по рисунку 2. При вычислении моментов сил 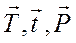относительно оси у проецируем каждую из этих сил на плоскость, проходящую через точку приложения силы перпендикулярно оси y.

Полученные проекция Tsin 30°, t sin 30°, P sin 15° параллельны оси z.

2. :

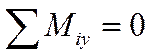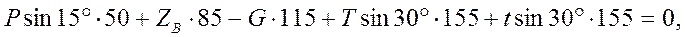
откуда

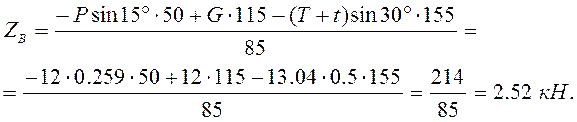
Аналогично при составлении уравнения 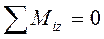находим проекции сил 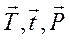на плоскости, перпендикулярные оси z. Эти проекции параллельны оси у и соответственно имеют абсолютные величины Tcos30^о, tcos30^о, Pcos15^о.

3. :

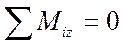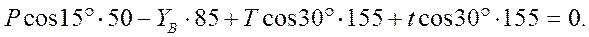
Определяем :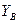

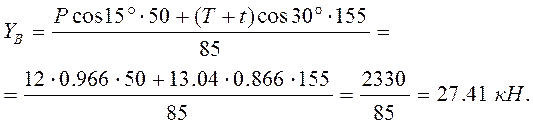
Составляем уравнения проекций на оси у и z (все действующие силы, перпендикулярные оси х, и уравнение 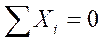преобразуются в тождество 0=0).

4.

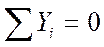
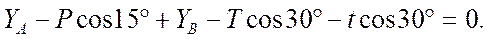
Находим Y_А:

:

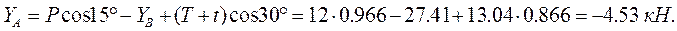
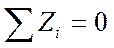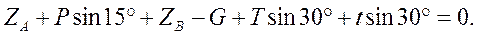
Определяем Z_А:

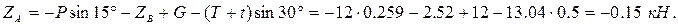
Задача 3. Прямоугольная однород­ная плита весом 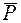удерживает­ся в горизонтальном положе­нии тросом СC’. Определить реакции связей, если Р = 100 Н, F = 40 Н, а = 30°, β = 60°, 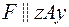(рис. 4).

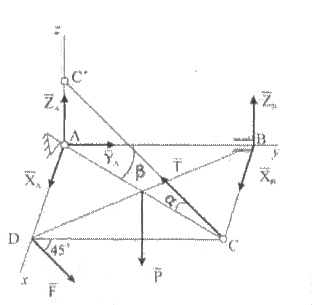
Рис.4

Решение. Используя прин­цип освобождаемоемости от свя­зей, заменим действие связей реакциями, приложенными к плите. В точке А (сферический шарнир) будут три состав­ляющие: 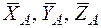. В точ­ке В — две составляющие: 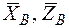. Реакцию нити 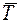направим по линии СС’. Для уравно­вешенной произвольной пространственной системы сил соста­вим шесть уравнений равновесия:

1.

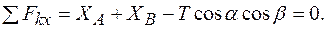
2.

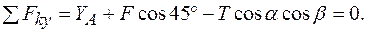
3.

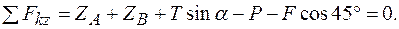
4.

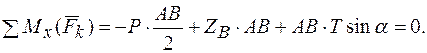
5.

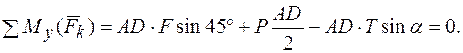
6.

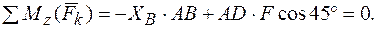
Из (6)

.

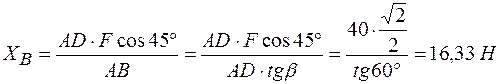Из (5)

.

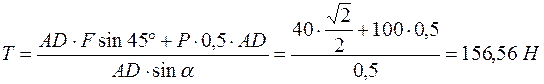Из (4)

.

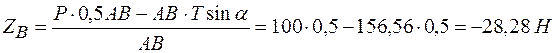Из (1)

.

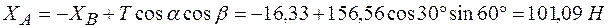Из (2)

.

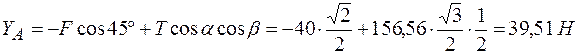Из (3)

.

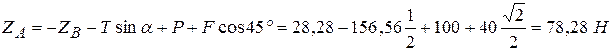Минус показывает, что направление 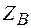противоположно направлению, показанному на рис 4.

Для пространственной системы параллельных сил можно со­ставить три уравнения равновесия. Если силы параллельны оси Z, то имеем следующие уравнения равновесия:

1. .

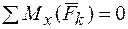2. .

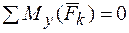3. .

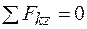Задача 4. Квадратная однород­ная плита весом Р нахо­дится в равновесии. Оп­ределить реакции связей, если Р = 100 Н; F = 20 H (рис. 5).

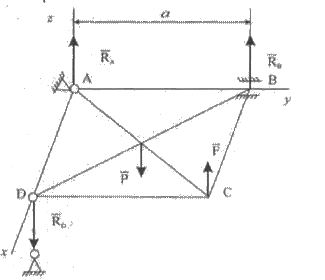
Рис. 5

Решение. Рассмотрим равновесие плиты под действием системы па­раллельных сил 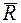, 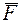и реакций связей 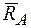, , 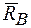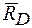. Составим три уравнения равно­весия:

1.

2.

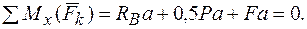
3.

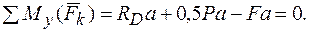
Находим из (2)

,

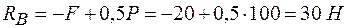из (3)

,

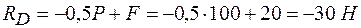из (1)

.

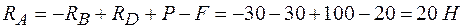Минус показывает, что реакция связей 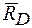направлена про­тивоположно направлению, показанному на рис. 5.

Задача. Горизонтальный вал весом G = 15 Н может вращаться в цилиндрических шарнирах А и В (рис. 4.3). К шкиву 1 приложено нормальное давление N и касательная сила сопротивления F = 0, 1 N.

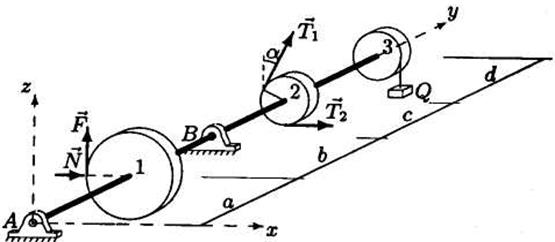
Рис. 4.3

На шкив 2 действуют силы натяжения ремней Т₁ = 30 Н, Т₂ = 57 Н. Груз Q = 18 Н висит на нити, навитой на шкив 3. Определить силу давления N и реакции шарниров в условии равновесия вала. Учесть веса шкивов: Р₁ = 35 Н, Р₂ = 10 Н, Р₃ = 15 Н. Все нагрузки действуют в вертикальных плоскостях. Известны радиусы шкивов, R ₁= 26 см, R ₂ = 10 см, R ₃ = 11 см и расстояния между характер­ными точками вала: а = 22 см, b = 25 см, с = 26 см, d = 26 см. Общая длина вала L = a + b + c + d; α =30°.