Квантовые размерные эффекты и условия их наблюдения.

1.1. Принцип размерного квантования. Понятие о плотности состояний в низкоразмерных системах.

Весь комплекс явлений, обычно понимаемый под словом электронные свойства низкоразмерных электронных систем, имеет в своей основе один фундаментальный физический факт – изменение энергетического спектра электронов и дырок в структурах с очень малыми размерами. Изменение физических и химических свойств частиц вещества, происходящих с изменением геометрических размеров частиц вещества, приводит к необходимости рассмотрения понятия ультрадисперсности. В общем случае под дисперсностью понимают степень раздробленности вещества на частицы. Чем меньше размер отдельной частицы, тем выше дисперсность. Большинство веществ окружающего нас мира существуют в виде дисперсных систем, которые по степени дисперсности частиц вещества можно разделить на три основные группы – грубодисперсные, высокодисперсные и ультрадисперсные. Ещё в XIX веке М. Фарадей впервые создал коллоидную суспензию золота, состоящую из крошечных частиц этого металла. При этом им было обнаружено, что цвет суспензии менялся на фиолетовый. Это в свою очередь свидетельствовало об изменении отражающих свойств суспензии при уменьшении размеров частиц. Повышенный интерес учёных к такого рода системам объясняется, прежде всего, тем, что уменьшение дисперсности частиц какого-либо вещества может приводить к заметным изменениям их свойств. Например, известно, что частицы серебра оказывают антибактериальное действие, однако только в последнее время стало известно, что в виде наночастиц активность серебра повышается в тысячи раз. Такие ультрадисперсные частицы как фуллерены и нанотрубки, своими удивительными свойствами также подтверждают тот факт, что многие вещества в наноформе не ведут себя таким же самым образом, как в своём привычном для нас виде. Особое внимание заслуживают так называемые ультрадисперсные системы, состоящие из частиц нанометрового масштаба. Вследствие размерного эффекта материалам в ультрадисперсном состоянии могут быть присущи уникальные сочетания химических, электрических, магнитных, тепловых, механических, сорбционных, радиопоглощающих и других свойств, не встречающихся в массивных телах. В отдельных малых частицах реализуются разнообразные размерные эффекты, наблюдается качественное изменение спектров элементарных возбуждений, чувствительных как к изменению симметрии, так и к наличию границ. Этим вызываются определённые аномалии в поведении электронов, фононов, плазмонов, магнонов и других элементарных возбуждений. Возможно, возникновение корреляций электронных состояний одновременно во многих частицах, что, по-видимому, важно для понимания сверхпроводящих свойств ультрадисперсных сред. Полвека тому назад Р. Фейнман для своей лекции о проблемах миниатюризации выбрал парадоксальное название «Внизу полным-полно места». Сегодня становится очевидным, какое значение имеют или будут иметь в будущем некоторые положения лекции Р. Фейнмана, прочитанной накануне 1960 года в Калифорнийском технологическом институте на Рождественском обеде Американского физического общества: «Речь идет о проблеме контроля и управления строением вещества в интервале очень малых размеров. Внизу (то есть «внизу или внутри пространства», если угодно) располагается поразительно сложный мир малых форм, и когда-нибудь (году, например, в 2000-м) люди будут удивляться тому, что до 1960 года никто не относился серьезно к исследованию этого мира... Поскольку для записи одного бита информации нам необходимо примерно 100 атомов, вся заботливо собранная человечеством книжная информация может быть «записана» в кубике металла с размером грани около 1/200 дюйма, представляющем крошечную, едва различимую человеческим глазом пылинку. Как видите, в глубинах пространства, внизу, полным-полно места и возможностей...

По мере уменьшения размеров мы будем постоянно сталкиваться с очень необычными физическими явлениями. Всё, с чем приходится встречаться в жизни, зависит от масштабных факторов... Внизу мы будем постоянно наблюдать новые закономерности и эффекты, предполагающие новые варианты использования».

В 2000 г. коллектив американских исследователей издал книгу «Нанотехнология в ближайшем десятилетии», целью которой являлось ознакомление американской общественности с состоянием нанотехнологических исследований к началу 1999 г. Нанонауку можно определить как совокупность знаний о свойствах вещества в нанометровом диапазоне. Нанотехнологию – как умение целенаправленно создавать объекты с заранее заданными составом, размерами и структурой в диапазоне приблизительно 1—100 нм. В последнее время было разработано достаточно большое число методов получения ультрадисперсных систем, позволяющих весьма тонко регулировать размеры частиц, их форму и строение. Эти методы могут быть разделены на две группы: диспергационные (механическое, термическое, электрическое измельчение или распыление макроскопической фазы) и конденсационные (химическая или физическая конденсация). Примерами ультрадисперсных систем являются нанопорошки, множество коллоидных систем, микроэмульсии и т.п. Размерные границы ультрадисперсности строго не определены, и в разных областях знания в это понятие вкладывается несколько различное количественное содержание. Итак, выше было дано понятие ультрадисперсности и показано, что с уменьшением размера частиц вещества его физические и химические свойства могут существенно меняться. Это происходит из-за того, что ход физических процессов зависит не только от свойств самого вещества, но и от геометрии той области пространства, в которой они протекают, то есть от размеров этой области. Для наглядной иллюстрации этой идеи следует обратиться к следующей аналогии: представим, что в узком переулке нужно развернуться какому-то транспортному средству. Очевидно, что мотоциклисту это будет сделать гораздо легче, чем водителю тяжёлого грузовика. Размерные эффекты в твёрдых телах – это явления, наблюдающиеся в условиях, когда геометрические размеры объекта сравнимы с длиной свободного пробега носителей заряда (электронов и дырок) или длиной волны де Бройля, определяющих протекание физических процессов. В зависимости от размеров исследуемого образца различают классические и квантовые размерные эффекты, которые могут влиять практически на любые свойства вещества. Очевидно, что для объектов нанометрового масштаба, где размеры частиц сравнимы с де Бройлевской длиной волны электрона, характерны именно квантовые размерные эффекты, определяющие такие свойства вещества, как теплоёмкость, электропроводность, некоторые оптические свойства. Самым ярким представителем квантовых размерных эффектов является туннельный эффект – чисто квантовое явление, сыгравшее важную роль в развитии современной электронике и приборостроении. Феномен туннелирования открыл в 1928 г. наш соотечественник Г. А. Гамов, впервые получив решения уравнения Шрёдингера, описывающие возможность преодоления частицей потенциального барьера, даже если её энергия меньше высоты барьера. Найденное решение объясняло многие экспериментальные данные и позволило понять большой круг явлений, происходящих при 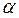- распаде ядра. Многие считают, что за грандиозность результатов его работ, ставших основополагающими для многих наук, Г.А. Гамов должен был быть удостоен нескольких Нобелевских премий. Лишь спустя тридцать лет после открытия Г. А. Гамова появились первые приборы на основе туннельного эффекта – туннельные диоды, транзисторы, датчики, термометры для измерения сверхнизких температур, и, наконец, сканирующие туннельные микроскопы, положившие начало современным исследованиям наноструктур. Идею размерного квантования достаточно удобным является показать, прибегая к элементарным модельным представлениям – модели одномерного потенциального ящика и далее для случая молекул линейных полиенов – модели свободного электрона (МСЭ). То обстоятельство, что в обычных условиях носители заряда сосредоточены в плёнке и не выходят из неё в окружающую среду, означает, что материал плёнки (например, полупроводник) представляет собой потенциальную яму для электронов глубиной, равной работе выхода 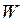, и шириной 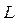. Согласно законам квантовой механики, энергия электронов в такой яме квантуется, т.е. может принимать лишь некоторые дискретные значения 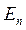, где 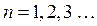принимая, таким образом, лишь целочисленные значения. Эти дискретные значения энергии называют уровнями размерного квантования. Типичные значения работы выхода в большинстве твёрдых тел имеют величину порядка 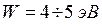, на несколько порядков превышающую характерную тепловую энергию носителей заряда 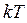, равную при комнатной температуре 0, 026 эВ, поэтому потенциальную яму можно в общем случае считать бесконечно глубокой. Другим необходимым условием, позволяющим считать яму бесконечно глубокой, является малость значений 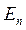, по сравнению с её действительной глубиной 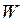. Это условие, которое для нижних уровней можно записать в виде:

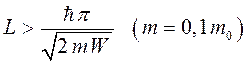
соответствует толщинам плёнки порядка нескольких межатомных расстояний. Во всех реальных структурах это условие соблюдается. Для лучшего понимания основной идеи размерного квантования в низкоразмерных электронных системах, рассмотрим некоторую плёнку, занимающую область .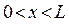

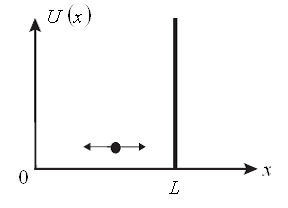
Рис.1. Одномерное движение частицы в одномерном потенциальном ящике

Пусть частица в такой плёнке свободно движется в жёстких пределах, например в интервале длиной 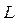, тогда соответственно:

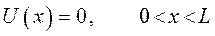
это означает, в свою очередь означает, что в концевых точках интервала, потенциальная энергия становится бесконечной.

Имеем, таким образом, соответственно:

Это и есть случай одномерного потенциального ящика. При таких граничных условиях частица с конечной энергией, не может вырваться за пределы данного интервала 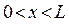, тогда уравнение Шрёдингера:

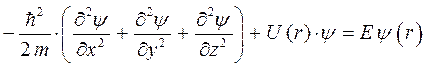
для рассматриваемого одномерного случая при 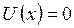, преобразуется к виду:

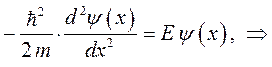
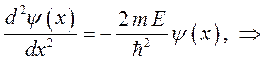
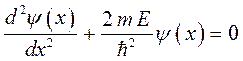
Последнее выражение аналогично полученному уже ранее уравнению:

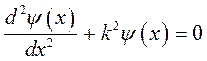
очевидно, что:

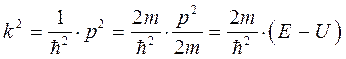
которое при граничном условии вида 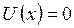, сводится к уравнению:

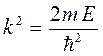
Действительно, учитывая уравнения, связывающие волновой вектор с импульсом микрочастицы:

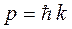
и её кинетической энергией:

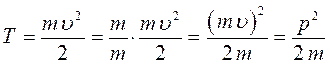
и таким образом:

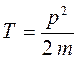
откуда:

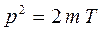
тогда:

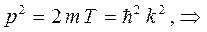
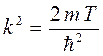
поскольку:

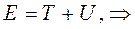
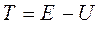
имеем соответственно:

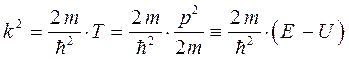
Поскольку при 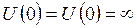, то вероятность нахождения электрона 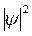, а, следовательно, и 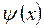вне указанного интервала, начиная с концов 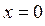и 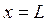, исчезает. Исходя из этих соображений, получаем краевые условия вида:

Для рассматриваемой задачи, решение уравнения Шрёдингера:

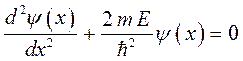
приводит к суперпозиции сопряжённых друг другу решений вида:

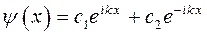
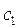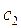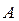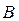Поскольку здесь коэффициенты и представляют собой амплитуды соответствующих стоячих волн и , тогда соответствующие решения волнового уравнения можно будет переписать в виде:

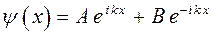
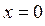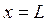В точках пространства и , уравнение Шрёдингера имеет тривиальное решение 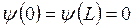. Это и есть дополнительные (граничные или краевые) условия для нахождения постоянных 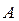и 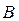. Из первого граничного условия 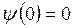находим соответственно:

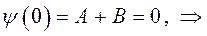
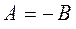
тогда:

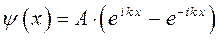
на основании формул Эйлера для показательной функции:

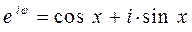
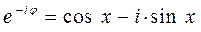
и эквивалентных им формул вида:

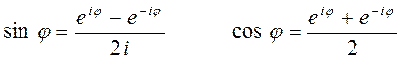
получаем для волновой функции тригонометрическое выражение вида:

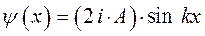
Заменив коэффициент 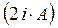в полученном выше выражении на общий нормировочный множитель 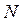, приходим к выражению вида:

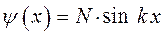
Для уточнения структуры волновой функции, подставим в последнее выражение значение координаты 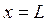. Учитывая второе граничное условие в точке 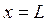и соответственно 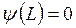, получим соответственно:

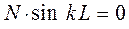
Полученное нами тригонометрическое уравнение имеет решение при условии, когда:

откуда следует, что:

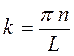
Условие вида 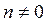принципиально, поскольку при 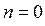волновая функция 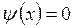не имеет физического смысла – частицы нигде нет (здесь 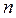- квантовое число). Таким образом, в потенциальной яме волновой вектор 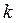, а, следовательно, и импульс 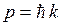принимает дискретный ряд значений:

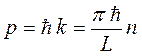
поскольку как было показано выше:

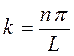
тогда волновая функция 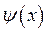приобретает вид:

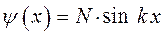
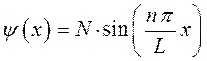
Нормировочный множитель 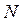найдём из условия нормировки (общий случай):

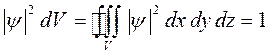
или для частного случая, в рамках рассматриваемой модельной задачи будем иметь соответственно:

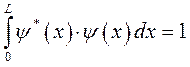
подставляя в подынтегральное выражение значение волновой функции:

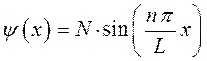
будем иметь соответственно:

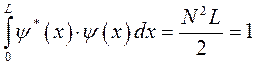
действительно:

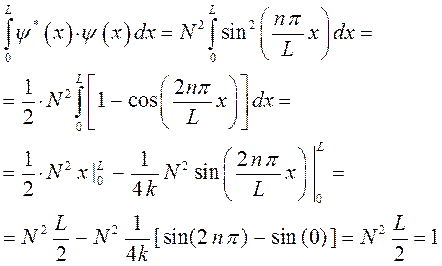
откуда следует, что:

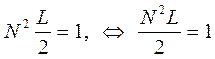
откуда:

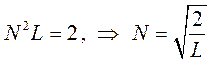
На основании проделанных выкладок, структура волновой функции частицы в потенциальной яме с бесконечно высокими стенками может быть уточнена и будет иметь вид:

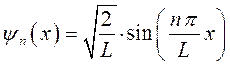
Графики волновых функций 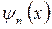и плотности вероятности частиц 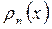принято изображать на диаграмме энергетических уровней, которые, в свою очередь, совмещают с графиком потенциальной энергии. Из представлений модели прямоугольного потенциального ящика непосредственно следует такое важное понятие как узловая точка – такая точка пространства, при переходе через которую волновая функция меняет свой знак на противоположный. Это в свою очередь является принципиальным, поскольку наличие или отсутствие последней определяет существование орбитального квантового числа . Так, с увеличением главного квантового числа 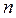, число узловых точек также увеличивается и принимает значение порядка 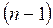. Чтобы найти узловые точки, волновую функцию приравнивают нулю:

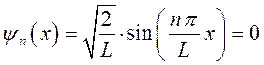
принимая, что:

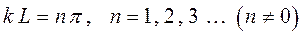
здесь:

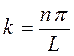
откуда следует соответственно, что:

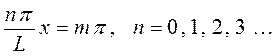
или после соответствующих преобразований имеем:

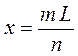
Используя полученное выше выражение, рассчитает количество узловых точек для каждого 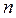. При этом ограничимся случаем 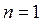, 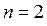и 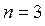. Для нижнего энергетического уровня с 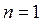, значения 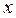равны: 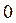, , 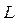, 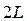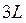… Однако по условию задачи частица, движущаяся в жёстких пределах 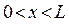, не может находиться за границей указанного интервала. Так, при 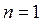волновая функция 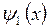узлов не имеет. Для следующего энергетического уровня с 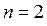, значения 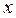равны соответственно: 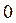, 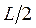и .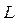

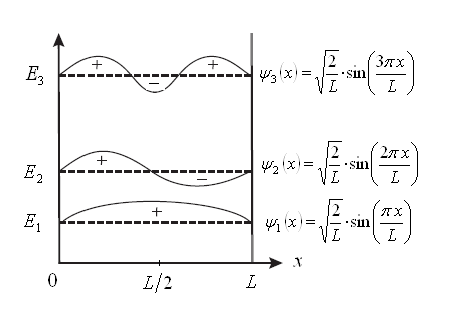
Рис.2. Волновые функции частицы в одномерном потенциальном ящике

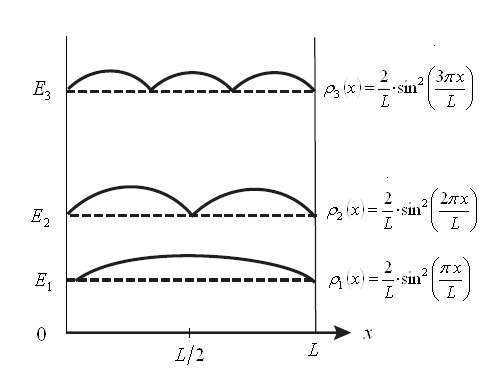
Рис.3. Плотности вероятности для частицы в одномерном потенциальном ящике

Однако узловой точкой здесь является точка 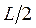. И наконец, для уровня с квантовым числом 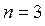получаем: 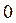, , 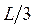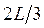и 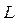. Здесь, для частицы, движущейся в пределах 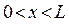, узловыми являются две точк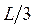и - и 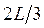. В общем случае для волновой функции 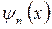число узлов будет очевидно равно 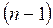, что хорошо видно из приведенных выше схем. Найдём теперь энергию частицы в потенциальном ящике. Так, частица свободно движется в пределах интервала 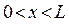, уравнение Шредингера, описывающее такое движение частицы, очевидно, будет иметь вид:

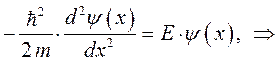
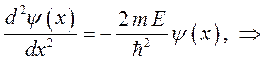
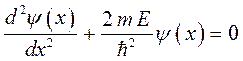
очевидно, данное уравнение будет иметь гармонические решения вида:

здесь 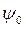представляет собой нормировочный множитель. Нетрудно убедиться, что данные решения действительно удовлетворяют уравнению:

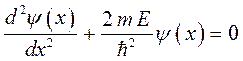
для этого вычислим первую и вторую производные от данных функций:

или в общем виде:

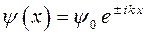
имеем соответственно:

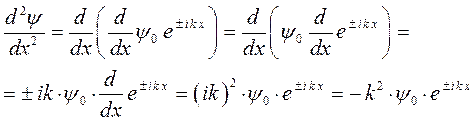
и далее:

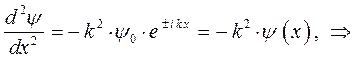
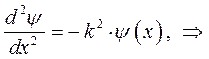
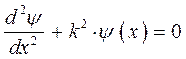
приравнивая между собой эквивалентные формы уравнения Шрёдингера для рассматриваемой одномерной задачи:

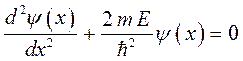
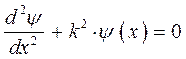
после преобразования последнего уравнения к виду:

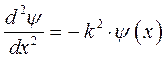
будем иметь соответственно:

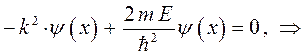
или что то же самое:

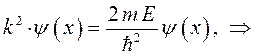
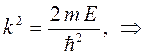
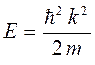
учитывая, что:

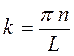
и соответственно:

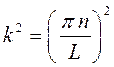
будем иметь:

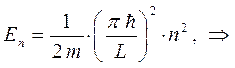
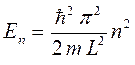
Поскольку свободное движение частицы совершается строго в пределах интервала 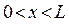, то очевидно, что выражение для энергии частицы в потенциальном ящике будет функцией параметра (квантового числа) 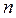, тогда соответственно:

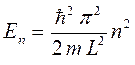
при :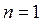

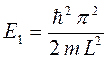
при :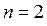

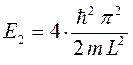
при :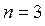

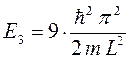
при :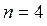

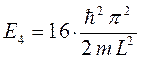
при :

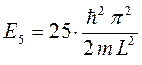
или в общем случае:

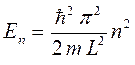
С учётом приведенных выше соображений, общее выражение для энергии частицы в одномерном потенциальном ящике приобретёт вид:

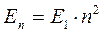
тогда значения энергий частицы в потенциальном ящике образуют ряд:

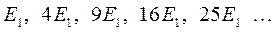
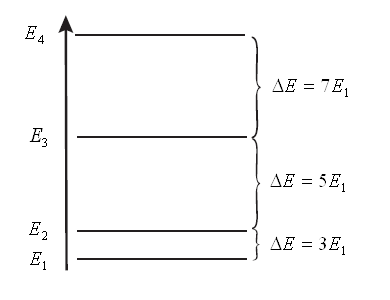
Рис.4. Диаграмма энергетических уровней частицы находящейся в одномерном потенциальном ящике.

это и означает, что энергия частицы в одномерном потенциальном ящике дискретная, квантованная величина. На основании полученных данных, легко построить диаграмму энергетических уровней частицы в одномерном потенциальном ящике и получить значения энергии перехода между двумя соседними уровнями. Действительно, из выражения вида:

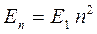
достаточно просто получить общее соотношение для энергии перехода между любыми двумя уровнями с квантовыми числам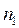и и :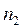

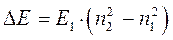
Необходимо отметить, что так называемые допустимые дискретные значения энергии частицы находящейся в прямоугольном потенциальном ящике можно также получить на основании полученных нами уже ранее выражений. Так, имеем соответственно выражение вида:

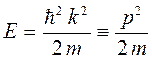
где

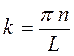
и соответственно:

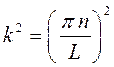
а также:

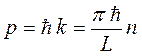
Сопоставляя между собой данные уравнения, приходим к выражению:

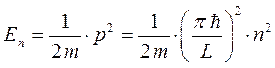
учитывая, что:

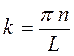
и соответственно:

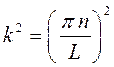
будем иметь:

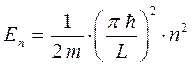
или что тоже самое:

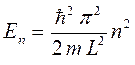
В этой задаче прослеживается характерная особенность квантово-механического подхода – квантование возникает как результат наложения на решение дифференциального уравнения определённых краевых условий. Как это следует из последнего выражения, расстояние между энергетическими уровнями будет зависеть от массы частицы 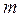и ширины ящика 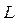. Действительно, имеем:

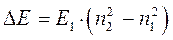
Очевидно, чем больше будет масса частицы и ширина ящика, тем больше будет величина 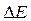. Тогда при условии 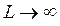энергетические уровни будут сближаться, а наименьшее значение энергии будет стремиться к нулю 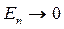. Это будет в свою очередь означать, что энергия теряет квантовый характер и становится непрерывной величиной, что приводит к исчезновению квантования. Итак, в рассматриваемой модельной задаче прослеживается одна характерная особенность квантово-механического подхода – квантование возникает как результат наложения на решение дифференциального уравнения определённых краевых условий. При этом полная энергия для частицы в потенциальной яме может иметь лишь дискретные, кратные значению 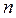энергии, т.е. квантуется. При этом что интересно, дискретность возникает как следствие решения уравнения Шрёдингера с учётом граничных (краевых) условий, т.е. отпадает необходимость введения каких либо постулатов, касающихся квантования физических величин, как это было, например, в случае теории Бора. Конечно, бесспорно, данная модель является довольно грубой, поскольку не учитывает эффекты межэлектронного взаимодействия, а также рассматривает только пространственную часть волновой функции без учёта её спиновой составляющей. Однако, тем не менее, не смотря на это, она позволяет на качественном уровне достаточно правильно отразить основную идею размерного квантования в низкоразмерных электронных системах, давая правильную интерпретацию понятия плотности состояний в низкоразмерных системах.

1.2. Условия наблюдения размерных эффектов.

Для того чтобы описанное в предыдущем разделе квантование энергетического спектра могло проявляться в каких-либо наблюдаемых эффектах, расстояние между энергетическими уровнями 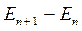должно быть достаточно велико. Во-первых, оно должно значительно превосходить тепловую энергию носителей заряда:

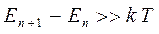
так как в противном случае практически одинаковая заселённость соседних уровней и частые переходы носителей заряда между ними делают квантовые эффекты ненаблюдаемыми. Если электронный газ вырожден и характеризуется энергией Ферми 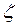, то желательно выполнение условия 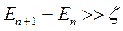. Предыдущее условие при этом выполняется автоматически, поскольку для вырожденного газа 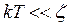. При невыполнении этого условия заполнено много квантовых уровней и квантовые размерные эффекты, будучи в принципе наблюдаемыми, имеют малую относительную величину. Существует ещё одно необходимое требование для наблюдения квантовых размерных эффектов. Так, в реальных структурах носители заряда всегда испытывают рассеяние на примесях, фононах. При этом интенсивность рассеяния обычно характеризуется временем релаксации импульса 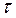и связанным прямой пропорциональностью с другой важной характеристикой – их подвижностью, которую можно описать на основании общей формулы вида:

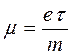
Величина 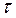представляет собой среднее время жизни того или иного состояния с данными фиксированными квантовыми числами.

В силу соотношения неопределённости, конечное значение 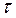влечёт за собой неопределённость в энергии данного состояния:

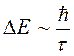
Очевидно, что говорить о наличии в системе отдельных дискретных уровней можно лишь в случае, когда расстояние между ними превышает неопределённость 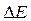, т.е. при выполнении условия вида:

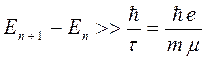
При этом можно показать, что выполнение данного требования эквивалентно требованию того, чтобы длина свободного пробега носителей заряда значительно превосходила размер области 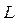, в которой происходит движение носителей заряда. Это достаточно очевидно. Так, согласно квантовой механике, квантование возникает при периодическом движении частицы. Это происходит лишь в случае достаточно слабого рассеяния, когда частица между двумя актами рассеяния (т.е. пройдя путь длиной ) успевает совершить несколько периодов колебаний, или, иными словами, несколько раз пересечь плёнку (нить или точку) от границы до границы. Поскольку расстояние между уровнями размерного квантования пропорционально 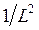. Действительно, учитывая, что:

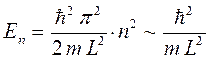
тогда на основании уравнений вида:

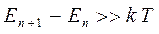
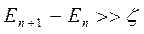
а также:

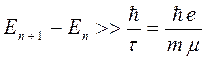
можно сделать вывод о том, что для наблюдения квантовых размерных эффектов необходимы малые размеры структур, достаточно низкие температуры и высокие подвижности носителей заряда, а также не слишком высокая их концентрация. Вот некоторые конкретные оценки. Так, чтобы наблюдать квантовые размерные эффекты в полупроводниках с 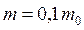(где 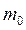- масса электрона) при температурах вплоть до комнатной, необходимо иметь 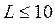нм. При этом подвижность носителей заряда должна заметно превосходить величину порядка 1000 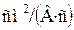. Если изготовить столь малые структуры не представляется возможным вследствие проблем технологического получения квантовых размерных структур, то наблюдение квантовых эффектов возможно лишь при пониженных температурах и требует более высоких подвижностей носителей заряда. Необходимо отметить также, что в соответствии с требованием:

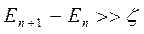
металлические структуры мало подходят для наблюдения размерных эффектов, поскольку величина энергии Ферми 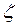в типичных металлах составляет несколько электрон-вольт, что заведомо больше любых расстояний между энергетическими уровнями. Полупроводниковые или полуметаллические структуры здесь будут явно предпочтительнее. Ещё одним важным условием, необходимым для наблюдения квантования, является высокое качество поверхностей, ограничивающих движение носителей заряда в квантовых ямах, нитях и точках. Для тонких плёнок речь идёт о внешней границе плёнки и о границе плёнка – подложка. Для гетероструктур, роль таких поверхностей играют гетеропереходы между различными полупроводниками. Характер отражения носителей от указанных границ должен быть близок к зеркальному, т.е. должен происходить с сохранением компоненты импульса, параллельной границе. Если это не так, то при каждом отражении от границы частица «забывает» о своём состоянии до отражения, т.е. на границе происходит эффективное рассеяние. Легко понять, что при этом длина свободного пробега становится равной 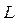и нарушается упомянутое выше условие 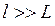. Для реализации зеркального отражения на границах необходимо, чтобы размеры шероховатостей, неизбежно существующих на любой из поверхностей, были меньше дебройлевской длины волны носителей заряда. Кроме того, границы не должны содержать высокой плотности заряженных центров, приводящих к дополнительному рассеянию.

1.3. Типы низкоразмерных систем и их свойства.

Поведение подвижных носителей заряда (электронов и дырок) в низкоразмерных структурах определяют три группы фундаментальных явлений: квантовое ограничение, баллистический транспорт и квантовая интерференция, а также туннелирование. Все эти эффекты по своему происхождению представляют собой типичные квантово-механические явления. Квантовое ограничение возникает, когда свободное движение электронов в одном из направлений оказывается ограниченным потенциальными барьерами. Запирание электрона с эффективной массой, по крайней мере, в одном из направлений, в соответствии с принципом неопределённости приводит к увеличению его импульса на величину 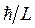. Соответственно увеличивается и кинетическая энергия электрона на величину

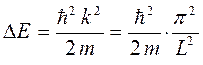
Таким образом, квантовое ограничение сопровождается как увеличением минимальной энергией запертого электрона, так и дополнительным квантованием энергетических уровней, соответствующих его возбуждённому состоянию. Это в свою очередь приводит к изменению спектра разрешённых энергетических состояний и влияет на перенос носителей заряда, что отражается на свойствах такой системы, которые существенно будут отличаться от объёмных свойств материала, из которого они сделаны. Так, свободный электрон, движущийся в трёхмерной системе (3D), имеет кинетическую энергию, величина которой в соответствии с пространственными компонентами его импульса 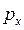, 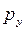и 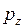составляет:

или в волновом представлении:

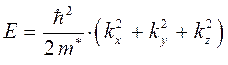
где - эффективная масса электрона (в твёрдых телах она обычно меньше, чем масса покоя электрона 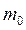); 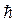- приведенная постоянная Планка (оператор Дирака); 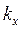, , 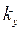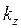- пространственные компоненты волнового вектора. Плотность электронных состояний при этом будет являться непрерывной функцией энергии:

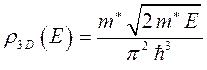
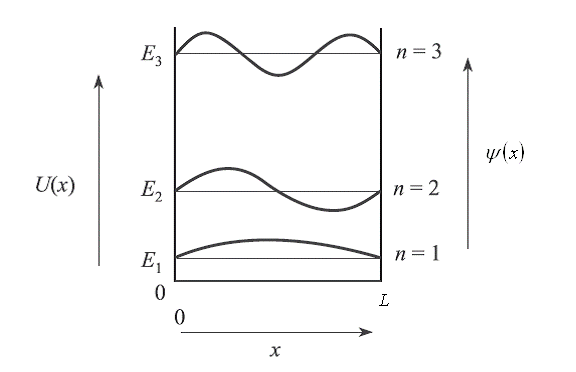
Рис.5. Потенциальная яма и волновые функции электрона в ней.

В низкоразмерной структуре свободное движение электрона ограничено, по крайней мере, в одном направлении. В данном направлении (пусть это будет направление вдоль оси 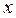) потенциальная энергия электрона может быть представлена в виде бесконечно глубокой потенциальной ямы. Если ширина ямы вдоль оси 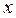равна 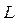, то в области 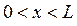электрон имеет нулевую потенциальную энергию, т.е. 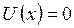. Бесконечно высокий потенциальный барьер делает невозможным нахождение электрона за границей этой области. Таким образом, волновая функция 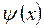электрона должна обращаться в нуль на границах потенциальной ямы, т.е. пр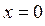и и 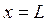. Такому условию отвечает лишь ограниченный набор волновых функций. Это – стоячие волны с длиной волны 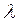, определяемой соотношением:

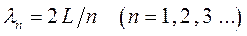
соответствующие разрешённые значения волнового вектора дискретны и равны:

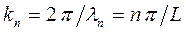
Как следствие, энергии разрешённых энергетических состояний электрона в яме также оказываются дискретными. Спектр этих состояний имеет вид:

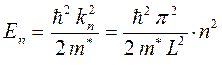
Таким образом, электрон, помещённый в ограниченную область пространства, например в область 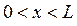, с граничными условиям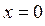и и 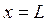, может занимать только дискретные энергетические уровни, называемые уровнями размерного квантования. Самое низкое состояние имеет энергию:

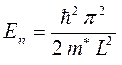
которая всегда больше нуля. Ненулевая минимальная энергия отличает квантово-механическую систему от классической, для которой энергия частицы, находящейся на дне потенциальной ямы, равна нулю. Кроме того, разрешённые значения энергии для электрона оказываются квантованными и пропорциональны величине .

Для того чтобы удовлетворить принципу неопределённости Гейзенберга:

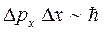
или если быть более точным:

в нашем случае 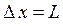, неопределённость импульса электрона должна быть:

что отвечает минимальному изменению энергии :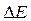

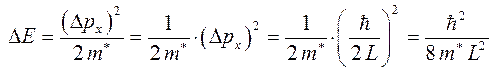
которое (с точностью до множителя 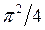) соответствует приведенному выше выражению для 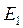. Таким образом, принцип неопределённости также приводит к выводу о ненулевом значении минимальной энергии электрона в потенциальном ящике (яме). Ограничение движения электронов (дырок) в низкоразмерных системах, приводящее (вследствие их корпускулярно – волновой природы) к ненулевому минимальному значению их энергии и дискретности энергий разрешённых состояний. Данный вывод строго доказывается в рамках соответствующих модельных представлений. В твёрдых телах квантовое ограничение может быть реализовано в трёх пространственных направлениях. Количество направлений, используется в качестве критерия для классификации элементарных низкоразмерных структур по трём группам: квантовые плёнки (плоскости), квантовые шнуры (проволоки или нити) и квантовые точки. В научной литературе для такого рода структур существуют также и другие названия. Так, квантовые плёнки (плоскости) называют ещё квантовыми ямами или двумерными (2D) электронными системами. Квантовые шнуры (проволоки или нити) называют одномерными (1D) электронными системами. Квантовые точки называют нульмерными (0D) электронными системами.

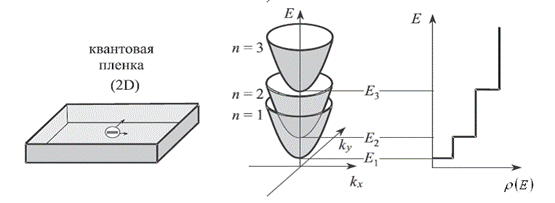
Рис.6. Двумерные (2D) электронные системы

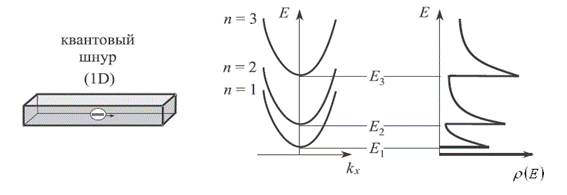
Рис.7. Одномерные (1D) электронные системы

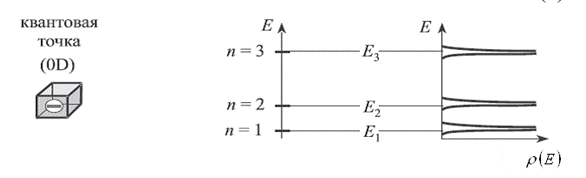
Рис.8. Нульмерные (0D) электронные системы

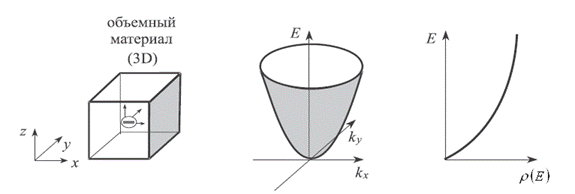
Рис.9. Трёхмерные (3D) электронные системы

Для примера, выше приведена схема трёхмерной системы (3D), представляющая собой материал с обычными свойствами фазы, то есть в своём обычном состоянии – таком, на электронную структуру которого не накладывается пространственных ограничений, как это имеет место в случае 2D, 1D и 0D типов структур.

Квантовые плёнки (плоскости) представляют собой двумерные (2D) структуры, в которых квантовое ограничение действует только в одном направлении – перпендикулярно плёнке. Обычно толщина такой структуры лежит в нанодиапазоне. Носители заряда в таких структурах могут свободно двигаться в плоскости 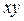. Энергия таких объектов складывается из квантованных значений, определяемых эффектом ограничения в направлении 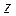(в соответствии с толщиной плёнки 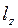), и непрерывных составляющих в направлени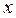и и :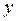

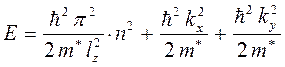
В 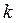- пространстве энергетическая диаграмма квантовой плёнки представляет собой семейство параболических зон, которые, перекрываясь, образуют подзоны. В общем случае минимальная энергия электрона в 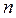- й подзоне задаётся соотношением вида:

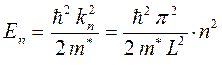
Электрон с такой энергией неподвижен в плоскости плёнки. Зависимость плотности электронных состояний от энергии в квантовой плёнке имеет ступенчатый вид (вместо параболической зависимости в трёхмерных структурах):

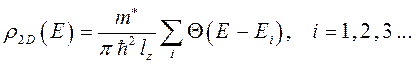
где 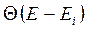- ступенчатая функция. Электроны в квантовых плёнках обычно называют двумерным электронным газом. Из-за малой толщины плёнок в таких структурах начинают проявлять себя квантовые эффекты, которые весьма сильно воздействуют на поведение электронов внутри квантовой плоскости, что позволяет произвольным образом менять физические и химические свойства таких веществ

Квантовые шнуры (проволоки или нити) представляют собой одномерные (1D) структуры, в которых квантовое ограничение действует уже не в одном, а в двух направлениях. Носители заряда в них могут свободно двигаться только в одном направлении – вдоль оси шнура. Таким образом, вклад в энергию носителя заряда дают кинетическая составляющая вдоль одного направления и квантованные значения в двух других направлениях:

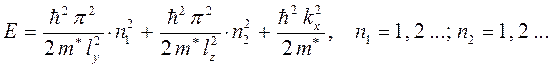
Для каждой пары дискретных уровней в направлениях квантового ограничения плотность электронных состояний в квантовом шнуре зависит от энергии по закону:

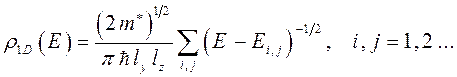
При нанесении таких структур на кристаллическую подложку, они позволяют изменять свойства кристаллов и создавать различные электропроводящие пути.

Квантовые точки представляют собой нульмерные (0D) структуры. В которых движение носителей заряда ограничено во всех трёх направлениях. В каждом из этих направлений энергия электрона оказывается квантованной в соответствии с формулой:

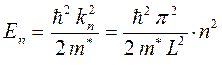
плотность же состояний представляет собой набор острых пиков, описываемых - функциями, т.е. имеем соответственно:

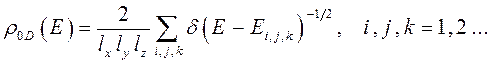
из-за сходства энергетических характеристик атомов и квантовых точек, последние иногда называют также «искусственными атомами». Квантовые точки состоят из сравнительно небольшого количества атомов. В этом отношении к ним близки атомные кластеры и нанокристаллиты (кристаллиты нанометровых размеров), где также имеет место эффект квантового ограничения. В оптическом спектре таких структур происходит постепенный переход от линейчатого спектра отдельных атомов к непрерывному поглощению объёмного материала. Этот эффект сегодня активно используется для формирования излучающих компонентов с чётко заданной шириной и формой полос испускания, что необходимо, к примеру, при производстве оптических сенсоров и лазеров с перестраиваемой длиной волны. Пионером в области создания приборов на таких структурах был русский учёный, академик Ж. И. Алфёров, ставший в 2002 г. Нобелевским лауреатом. Вслед за Нобелевской премией Алфёров получил и государственную за фундаментальные исследования процессов формирования и свойств гетероструктур с квантовыми точками и создание лазеров на их основе. Ввиду малости величины квантовой точки, на её основе можно строить различные полупроводниковые устройства, использующие для своей работы квантовые размерные эффекты. Лазеры нового поколения, основанные на гетероструктурах с квантовыми точками прекрасно работают, подтверждая старую истину, что в науке нет нерушимых догм. Ведь долгое время считалось, что вырастить кристалл с кусочками другого материала внутри без дефектов невозможно. То, что сделали сотрудники лаборатории Ж.И. Алфёрова, можно смело назвать революцией в лазерной физике. Если раньше учёные, выращивая кристаллы для лазеров, вынуждены были полностью управлять процессом, то теперь ситуация иная – нужная структура растёт сама. Всё дело в новой технологии выращивания материала, – говорит академик Алфёров. Традиционно гетероструктурные материалы, например, из арсенида галлия и арсенида индия, получают, накладывая слой за слоем. Много лет назад, начиная эти исследования, мы наносили слои друг на друга вручную. Эта работа требовала огромного внимания и напряжения. Но теперь мы решили эту задачу, и уже сама природа помогает нам получать в процессе выращивания различные ансамбли таких квантовых точек. Дело в том, что если правильно подобрать все параметры: температуру, скорость осаждения, соотношение потоков атомов, то кристалл вырастет без дефектов. Это позволяет радикально улучшить свойства полупроводниковых приборов. Один из участников работы Н. Леденцов, выступая на международном семинаре «Нанотехнологии в физике, химии и биотехнологии», пошутил, что теперь, зная законы роста наноматериалов, можно и поразвлечься: расположить квантовые точки в виде блюдец, сплести бусы из точек, создать большие и маленькие наноостровки. За этой шуткой большое будущее – варьируя расположение квантовых точек, можно изменять и корректировать свойства кристалла. Рассмотренные элементарные низкоразмерные структуры в определённом смысле являются идеализированными объектами. Очевидно, что низкоразмерные структуры, представляющие практический интерес, должны располагаться на какой-либо подложке и иметь контакт с другими структурами и функциональными элементами. Более того, приборные применения требуют комбинации нескольких элементарных структур. Тем не менее, несмотря на появление в сложных комбинированных структурах новых размерных эффектов, определяющую роль в них по-прежнему продолжает играть квантовое ограничение.

1.4. Перспективы использования размерных эффектов в электронике.

В настоящее время вычислительная техника подошла к пределу своих возможностей по быстродействию компьютеров и размеру микросхем. Масштаб порядка 0, 1 мкм определяет границу применимости законов классической физики, и при дальнейшем увеличении быстродействия и уменьшении размеров мы попадаем в мир нанометрового масштаба, где доминируют квантовые размерные эффекты. Поэтому для решения задач конструирования компьютеров нового поколения требуется принципиально новый подход. В последние годы стала широко обсуждаться идея использования квантовых размерных эффектов для хранения и обработки информации, поэтому квантовые точки привлекают всё большее внимание. Электроны в квантовых точках локализованы, поэтому энергетический спектр каждой такой квантовой точки будет являться дискретным, как у отдельно взятого атома. Мы привыкли к тому, что ЭВМ оперирует с числами, выраженными в двоичной форме, т.е. состоящими из набора нулей и единиц. На заре развития вычислительной техники логические элементы ЭВМ выполнялись на основе реле (ключ разомкнут – 0, ключ замкнут – 1), потом на смену реле пришли электронные лампы, а затем – полупроводниковые структуры. Все перечисленные электронные устройства являются, по сути дела, объектами макромира, поскольку для выполнения ими своих функций требуется наличие макроскопического числа электронов (более чем 10⁶). Один отдельно взятый электрон обладает одной удивительной характеристикой – наличием спина, или собственным вращательным моментом. При этом возможны только два таких состояния, которым отвечают два значения спинового квантового числа 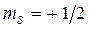и . 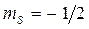Электрон может таким образом быть естественным кандидатом для представления чисел в двоичной форме. Действительно, приписав электронам со спином 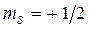и 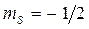соответственно логическую единицу и логический нуль, можно каждой конкретной спиновой конфигурации системы электронов поставить в соответствие определённый набор таких нулей и единиц, т.е. определённое число, записанное в двоичной форме, или другими словами, определённую информацию (при этом один электрон является носителем одного бита информации). Однако наличия соответствия между знаком спина электрона и логическими переменными (нулями и единицами) недостаточно для конструирования конкретных вычислительных схем и устройств. Нужно найти какие-то реальные способы ввода, хранения, обработки и вывода спиновой информации. Прежде же всего необходимо научиться локализовать отдельные электроны в небольших областях пространства (чем меньше будут размеры этих областей, тем выше будет плотность информации, и тем больше логических элементов можно будет разместить в единице объёма или на единице площади). На современном уровне развития технологии для этой цели как нельзя лучше подходят квантовые точки. В каждую пирамидку из атомов можно внедрить произвольное число электронов. При этом движение электрона в квантовой точке будет ограничено во всех трёх направления, и энергетический спектр будет являться полностью дискретным, как в отдельном атоме. Таким образом, дискретность электронных состояний в квантовой точке и наличие у него собственного вращательного момента – спина – могут быть использованы при конструировании сверхминиатюрных логических элементов, которые в скором времени, будем надеяться, станут основой нового поколения ЭВМ. Так, компания HP уже провозгласила стратегию создания наноэлектроники на основе квантовых размерных эффектов и молекулярных компьютеров. Издавна люди мечтали о телепортации – мгновенном перемещении в пространстве. Так, герои народных сказок оказываются в тридесятом царстве, надев волшебное колечко, а компьютерные игры и фантастика кишат порталами и прыжками в гиперпространстве. Известен так называемый парадокс Эйнштейна – Подольского – Розена (ЭПР - парадокс), заключающийся в том, что если после взаимодействия двух квантовых частиц провести наблюдения за одной из них, то мгновенно изменятся параметры другой, уже далеко отлетевшей частицы. Эксперименты показали, что частицы проявляют удивительную взаимосогласованность даже на таких больших расстояниях, на которых они никак не могли бы повлиять друг на друга с точки зрения классической теории. Проблема заключается в так называемой нелокальности волновой функции для системы из нескольких частиц – несмотря на то, что частицы уже далеко друг от друга, вероятности нахождения их в том или ином состоянии остались взаимосвязанными после квантового взаимодействия. Это казалось фантастикой, пока Антон Цойлингер и Франческо де Мартини не передали состояние поляризации между двумя фотонами при помощи третьего фотона на расстояние 10 км. Достигнув успехов в телепортации фотонов, экспериментаторы уже планируют работы с другими частицами – электронами, атомами и ионами. Телепортация сможет обеспечить надёжную передачу и хранение данных на фоне общих помех, когда все другие способы оказываются неэффективными. Возможно, в будущем сети квантовой телепортации получат такое же распространение, как современные телекоммуникационные сети. Однако в отличие от передачи информации на расстояние, которым уже никого не удивишь, обычно считают, что невозможно переместить какой-либо материальный объект или даже человека, поскольку при этом необходимо переместить все частицы, из которых он состоит. Поскольку квантовые частицы неотличимы друг от друга, их можно не перемещать, а собрать телепортируемый объект из новых частиц на основе полученной информации (например, при помощи молекулярных сборщиков – ассемблеров). Следовательно, телепортация объекта есть телепортация квантовых состояний частиц и воссоздание их на удалённом расстоянии. Так можно было бы, и копировать объекты, но в силу принципа неопределённости, чем больше получено информации о некотором объекте, тем больше искажений будет вноситься в этот объект – и так до тех пор, пока исходное состояние не будет разрушено полностью. Как только будет считана вся нужная информация, объект исчезнет и снова появится вновь после соответствующей квантовой сборки. Экспериментальные подтверждения справедливости квантовой механики столь убедительны, что должны были развеять всякое недоверие к ней. Однако всё же остаётся нерешённым нравственный аспект данной проблемы. Так, хорошо известно, что и Эйнштейн, и Шрёдингер, и де Бройль, которые были творцами новой механики, высказывались против понимания сущности теории на основе принципа неопределённости. «Бог не играет в кости…» - так Эйнштейн отзывался о вероятностной трактовке волновой функции. Однако в своей работе физики всегда имеют дело с несовершенными теориями, справедливыми только для ограниченного круга явлений, ровно до тех пор, пока не появляется новая, более общая теория. Так, например, две с половиной тысячи лет назад, атом считался неделимым. Вплоть до XV века че