
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аналітичне вирівнювання рядів динаміки
|
|
Аналітичне вирівнювання є більш досконалим способом обробки часових рядів, який дає можливість не тільки гарантовано (хоча інколи й не дуже надійно) виявляти тенденцію та її характер, але й робити прогноз розвитку явища на наступні часові моменти або інтервали. Метод застосовний для рівномірних інтервальних рядів і для моментних рядів з довільними проміжками δ і часу між моментами.
Суть методу полягає в тому, що кожний фактичний рівень уі ознаки Y розглядається як сума двох доданків: 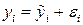 , де
, де 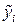 – систематична складова, яка відображає загальну тенденцію і виражається рівнянням
– систематична складова, яка відображає загальну тенденцію і виражається рівнянням 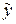 = f(t);
= f(t);  – випадкова складова, яка відображає флуктуації рівнів ряду і завуальовує загальну тенденцію.
– випадкова складова, яка відображає флуктуації рівнів ряду і завуальовує загальну тенденцію.
Таким чином, аналітичне вирівнювання динамічного ряду означає побудову функції 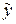 = f(t), яка аналітично виражає залежність систематичної складової значень ознаки Y від часу t. При цьому для інтервальних часових рядів аргумент t звичайно являє собою порядковий номер інтервалу. Нумерацію будемо починати з нуля.
= f(t), яка аналітично виражає залежність систематичної складової значень ознаки Y від часу t. При цьому для інтервальних часових рядів аргумент t звичайно являє собою порядковий номер інтервалу. Нумерацію будемо починати з нуля.
Такі функції і їх графіки називають трендовими кривими. За допомогою трендової кривої завжди можна встановити тенденцію розвитку явища, її характер, а також зробити прогноз на наступні часові інтервали або моменти.
Процедура побудови трендової кривої складається з двох етапів: 1) вибір виду функції f(t); 2) обчислення параметрів вибраної функції.
З формально-математичної точки зору побудова трендової кривої цілком аналогічна побудові рівняння регресії, що детально розглядалось у п. 2.4 л. р. № 3, за винятком двох моментів:
1. Якщо ряд є рівномірним і неперервним, то системи лінійних алгебраїчних рівнянь (3.9), (3.10) можна суттєво спростити. Для цього необхідно: а) усі часові моменти ti моментного ряду пронумерувати, починаючи з нуля, і надалі моменти ti ототожнювати з їх номерами (як і часові інтервали для інтервального ряду): ti = і, і = 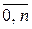 ; б) перейти до умовних номерів
; б) перейти до умовних номерів 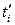 , перенумерувавши часові інтервали або моменти так, щоб точка відліку опинилась у середині часового ряду. Схематично це може виглядати, наприклад, так:
, перенумерувавши часові інтервали або моменти так, щоб точка відліку опинилась у середині часового ряду. Схематично це може виглядати, наприклад, так:
– для непарного числа (п +1) рівнів ряду: 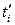 = ti – п/ 2 (n= 2 l,
= ti – п/ 2 (n= 2 l, 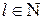 ),
),
| Фактичні номери ti | |||||
Умовні номери 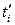
| –2 | –1 |
– для парного числа (п +1) рівнів ряду: 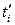 =2 ti – п (n= 2 l +1,
=2 ti – п (n= 2 l +1, 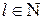 ),
),
| Фактичні номери ti | ||||||
Умовні номери 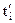
| –5 | –3 | –1 |
Очевидно, що 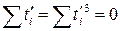 , за рахунок чого і спрощуються системи рівнянь. Зокрема, система (3.9) для умовних параметрів а 1і b 1 набуває вигляду
, за рахунок чого і спрощуються системи рівнянь. Зокрема, система (3.9) для умовних параметрів а 1і b 1 набуває вигляду
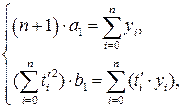 (4.19)
(4.19)
звідки
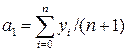 ,
,  . (4.20)
. (4.20)
Система (3.10) для умовних параметрів p 1, q 1i r 1 набуває вигляду
 (4.21)
(4.21)
звідки 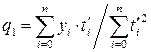 , що збігається з відповідною формулою (4.20), а параметри p 1 i r 1 знаходяться як розв’язок системи двох лінійних рівнянь, що складається з першого і третього рівнянь системи (4.21).
, що збігається з відповідною формулою (4.20), а параметри p 1 i r 1 знаходяться як розв’язок системи двох лінійних рівнянь, що складається з першого і третього рівнянь системи (4.21).
Після розв’язання систем (4.19) і (4.21) одержуємо лінійну та квадратичну (або параболічну) моделі тренду відповідно
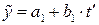 та
та 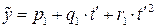 , (4.22)
, (4.22)
як функції умовного часу  .
.
Для переходу до фактичного часу t необхідно в рівняннях (4.22) замість  покласти:
покласти:  = t–l для непарного числа рівнів ряду, де l=n /2;
= t–l для непарного числа рівнів ряду, де l=n /2;  =2 t–п для парного числа рівнів ряду. В результаті одержимо лінійну та квадратичну моделі тренду відповідно
=2 t–п для парного числа рівнів ряду. В результаті одержимо лінійну та квадратичну моделі тренду відповідно
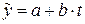 та
та  , (4.23)
, (4.23)
де a=a 1 – b 1 · l, b=b 1, p=p 1 – q 1 · l+r 1· l2, q=q 1 – 2r 1· l, r=r 1 для непарного числа (n +1); a=a 1 – b 1 · п, b=2b 1, p=p 1 + q 1 · п+r 1 · n2, q=2q 1 – 4r 1 · n, r=4r 1 для парного числа (n +1).
2. Регресійна дисперсія обчислюється за формулою
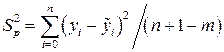 , (4.24)
, (4.24)
де 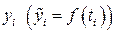 – фактичні (вирівняні) значення рівнів ряду; (п +1) – число рівнів ряду; п – номер останнього рівня ряду, якщо нумерація починається з нуля; т – число параметрів трендової кривої.
– фактичні (вирівняні) значення рівнів ряду; (п +1) – число рівнів ряду; п – номер останнього рівня ряду, якщо нумерація починається з нуля; т – число параметрів трендової кривої.