
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пирамида
|
|
Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, - вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.
Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания (рис. 49)
Пирамида называется п – угольной, если ее основанием является п – угольник. Треугольная пирамида называется также тетраэдром.
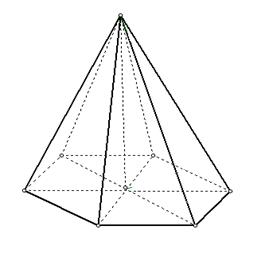
 вершина
вершина
 грань
грань
 высота
высота
 основание
основание
Рис.49
Пирамида называется правильной, если в ее основании лежит правильный многоугольник, а высота проектируется в центр основания
Боковые грани правильной пирамиды - равные равнобедренные треугольники.
Боковые ребра правильной пирамиды равны.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой (рис.50)
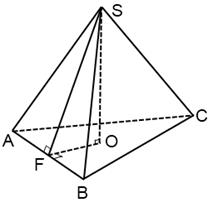
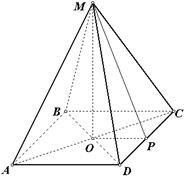 MP, SF – апофема
MP, SF – апофема
Рис.50
Задачи
 Цель. Учиться изображать основные многогранники, выполнять чертежи по условиям задач; решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов), использовать при решении стереометрических задач планиметрические факты и методы.
Цель. Учиться изображать основные многогранники, выполнять чертежи по условиям задач; решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов), использовать при решении стереометрических задач планиметрические факты и методы.
1.По данной стороне основания а и боковому ребру высоту правильной пирамиды:
1) треугольной; 2) четырехугольной.
2.Высота правильной четырехугольной пирамиды равна 7 см, а сторона основания 8 см. Определить боковое ребро.
3. Основанием пирамиды служит параллелограмм, у которого стороны содержат 3 см и 7 см, а одна из диагоналей 6 см. Высота пирамиды, проходящая через точку пересечения диагоналей основания, равна 4 см. Определить боковые ребра пирамиды.
4. Основанием пирамиды служит равнобедренный треугольник, у которого основание равно 6 см и высота 9 см. Боковые ребра равны между собой, и каждое содержит 13 см. Определить высоту этой пирамиды.
5.По данной стороне основания а и высоте h найти полную поверхность правильной пирамиды: 1) треугольной; 2) четырехугольной.
6.Определить боковую поверхность правильной треугольной пирамиды, если ее высота равна 4 см, а апофема 8 см.
 |
7.Определить высоту правильной треугольной пирамиды, если сторона основания равна а, а боковая поверхность вдвое больше площади основания
8.В правильной четырехугольной пирамиде боковая поверхность равна 14, 76 м2, а полная поверхность 18 м2.Определить сторону основания и высоту пирамиды.
9.Определить боковую поверхность правильной треугольной пирамиды, если сторона основания равна а и боковое ребро составляет с плоскостью основания угол в 450.
10.Определить сторону основания и апофему правильной треугольной пирамиды, если ее боковое ребро и боковая поверхность соответственно равны 10 см и 144 см2
Ответы к задачам
1.1) 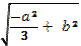 , 2)
, 2) 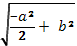 , 2. 9 см. 3.5см и 6 см. 4. 3см. 6.288 см2. 7.
, 2. 9 см. 3.5см и 6 см. 4. 3см. 6.288 см2. 7.  а. 8.1, 8 м и 4 м.
а. 8.1, 8 м и 4 м.
9. а2 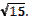 10.16 см и 6 см 12 см и 8 см.
10.16 см и 6 см 12 см и 8 см.