Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
В пространстве, как и на плоскости, вектором называется направленный отрезок.
|
|
Координатами вектора с началом в точке А1(х1; у1; z1) и концом в точке А2 (х2; у2; z2) называются числа х2 – х1, у2 – у1, z2 – z1.
Равные векторы имеют равные координаты, и обратно. Это дает основание для обозначения вектора его координатами: 
Модуль вектора  заданного своими координатами: заданного своими координатами:
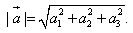
|
При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т.е. справедливы формулы:
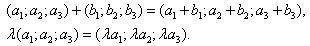
|
Скалярным произведением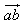 векторов векторов 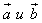 называется число: называется число:
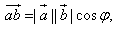 где
где 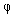 - угол между векторами - угол между векторами
|
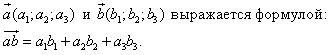 Скалярное произведение векторов Скалярное произведение векторов
|
Косинус угла между векторами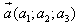 и и 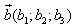 находится по формуле: находится по формуле:
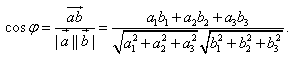
|
Необходимое и достаточное условие перпендикулярности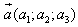 векторов и векторов и 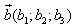 имеет вид: имеет вид:
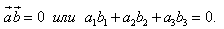
|
Задача 1. Даны четыре точки А (2; 7; -3), В(1; 0; 3), С(-3; -4; 5), D(-2; 3; -1). Укажите среди векторов 
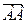 ,
, 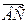 ,
, 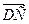 ,
, 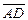 ,
, 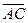 и
и 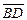 равные векторы
равные векторы
Решение. Надо найти координаты указанных векторов и сравнить соответствующие координаты. У равных векторов соответствующие координаты равны. Например, у вектора 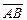 координаты: 1 – 2 = -1, 0 – 7 = -7, 3 – (- 3) = 6. У вектора
координаты: 1 – 2 = -1, 0 – 7 = -7, 3 – (- 3) = 6. У вектора 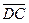 такие же координаты: -3 – (-2) = -1, -4 – 3 = -7, 5 – (- 1) = 6. Таким образом, векторы
такие же координаты: -3 – (-2) = -1, -4 – 3 = -7, 5 – (- 1) = 6. Таким образом, векторы 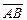 и
и 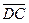 равны. Другой парой равных векторов будут
равны. Другой парой равных векторов будут 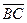 и
и 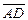 .
.
Задачи
Цель. Учиться использовать координатный метод для определения взаимного расположения векторов в пространстве; использовать при решении стереометрических задач планиметрические факты и методы; проводить доказательные рассуждения в ходе решения задач.

1.Даны три точки А (1; 0; 1), В (-1; 1; 2), С (0; 2; -1). Найдите точку D(х; у; z), если векторы 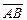 и
и 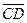 равны.
равны.
2.Даны векторы (2; п; 3) и (3; 2; т). При каких значениях т и п эти векторы коллинеарны?
3.При каком значении п данные векторы перпендикулярны:
1) а (2; -1; 3), в (1; 3; п),
2) а (п; -2; 1), в (п; -п; 1), 3) а (п; -2; 1), (п; 2 п; 4), 4) а (4; 2 п; -1), в (-1; 1; п)?
4.Даны три точки А (1; 0; 1), В (-1; 1; 2), С (0; 2; -1). Найдите на оси z такую точку D (0; 0; с), чтобы векторы 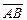 и
и 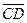 были перпендикулярны.
были перпендикулярны.
 |
5.Даны четыре точки А (0; 1; -1), В (1; -1; 2), С (3; 1; 0), D (2; -3; 1). Найдите косинус угла φ между векторами 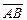 и
и 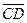 .
.
6. Даны три точки А (0; 1; -1), В (1; -1; 2), С (3; 1; 0). Найдите косинус угла С треугольника АВС.
Ответы к задачам
1. D (-2; 3; 0).2. п = 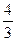 3. 1) п =
3. 1) п = 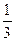 , 2) п = -1, 3) п = 2, 4) п = 4. 4. c = 1. 5.
, 2) п = -1, 3) п = 2, 4) п = 4. 4. c = 1. 5. 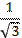 . 6.
. 6.