
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введение декартовых координат в пространстве
|
|
Возьмем три взаимно перпендикулярные прямые x, y, z, пересекающиеся в точке O. Через каждую пару прямых проведем плоскости. Получим три плоскости xy, xz и yz.
Данные прямые x, y и z называются координатными осями.
Плоскости xy, xz и yz называются координатными плоскостями.
Точка O - точка пересечения прямых x, y и z называется началом координат (рис.31)
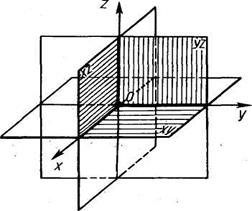
Рис 31
Координатой x точки A называется число, равное абсолютной величине длине отрезка OAx: положительное, если точка Ax лежит на положительной полуоси x, отрицательное, если на отрицательной полуоси. Аналогично можно определить координаты у и z
Координаты точки A в пространстве записываются так: A(x; y; z) (рис.32)
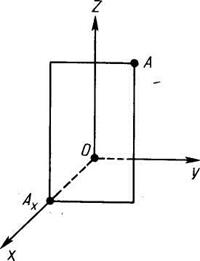
Рис.32
Основные формулы
Расстояние между точками A 1(x1; y1) и A2 (x2; y2):
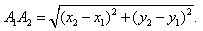
|
Координаты (x; y) середины отрезка с концами A1 (x1; y1) и A2 (x2; y2)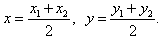
|
Задача 1. Даны точки А(1; 2; 3), В(0; 1; 2), С(0; 0; 3), D(1; 2; 3). Какие из этих точек лежат: 1) в плоскости ху; 2) на оси z; 3) в плоскости уz?
Решение. У точек плоскости ху координата z равна нулю. Поэтому только точка Dлежит в плоскости ху. У точек плоскости уzкоордината zравна нулю. Следовательно, точки В и С лежат в плоскости уz. У точек на оси z две координаты (х и у) равны нулю. Поэтому только точка С лежит на оси z.
Задача 2. В плоскости ху найти точку D, равноудаленную от трех точек: А (0; 1; --1),
В (-1; 0; 1), С (0; -1; 0)
Решение:
АD2 = (х – 0)2 + (у – 1)2 + (0 + 1)2,
ВD 2 = (х+ 1)2 + (у – 0)2 + (0 - 1)2,
СD2 = (х – 0)2 + (у + 1)2 + (0 - 0)2.
Приравнивая первые два расстояния третьему, получим два уравнения для определения х и у:
-4у + 1 = 0, 2х – 2у + 1 = 0. Отсюда х = 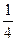 ; у = -
; у = - 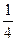 . Искомая точка D (
. Искомая точка D (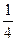 ; -
; - 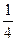 ; 0)
; 0)
Задачи
Цель. Учиться находить координаты точек пространства, использовать при решении стереометрических задач планиметрические факты и методы; проводить доказательные рассуждения в ходе решения задач.

1.Найдите расстояния от точки (1; 2; -3) до: 1) координатных плоскостей; 2) осей координат; 3) начала координат
2.На оси х найдите точку С (х; 0; 0), равноудаленную от двух точек А (1; 2; 3) и В (-2; 1; 3)
3.Докажите, что четырехугольник АВСD с вершинами в точках А (1; 3; 2), В (0; 2; 4),
С (1; 1; 4), D (2; 2; 2) является параллелограммом
4. Даны один конец отрезка А (2; 3; -1) и его середина С (1; 1; 1). Найдите второй конец отрезка В (х; у; z).
 5.Найдите координаты вершины D параллелограмма, если координаты трех других его вершин известны: 1) А (2; 3; 2), В (0; 2; 4), С (4; 1; 0); 2) А (1; -1; 0), В (0; 1; -1), С (-1; 0; 1); 3) А (4; 2; -1), В (1; -3; 2), С (-4; 2; 1)
5.Найдите координаты вершины D параллелограмма, если координаты трех других его вершин известны: 1) А (2; 3; 2), В (0; 2; 4), С (4; 1; 0); 2) А (1; -1; 0), В (0; 1; -1), С (-1; 0; 1); 3) А (4; 2; -1), В (1; -3; 2), С (-4; 2; 1)