Теорема 2.11. Признак перпендикулярности двух плоскостей

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны (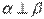) (рис.28)

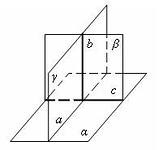
Рис.28

α – плоскость, в – перпендикулярная ей прямая, β – плоскость, проходящая через прямую в, и с – прямая, по которой пересекаются плоскости α и β.

Следствие. Если плоскость перпендикулярна к линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей

Задача 1. Доказать, что через любую точку прямой в пространстве можно провести две различные перпендикулярные ей прямые.

Доказательство:

По аксиоме I существует точка, не принадлежащая прямой а. По теореме 2.1через точку В и прямую а можно провести плоскость α. (рис.29) По теореме 2.3 через точку А в плоскости α можно провести прямую 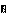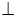а. По аксиоме С₁ существует точка С, не принадлежащая α. По теореме 15.1 через точку С и прямую а можно провести плоскость β. В плоскости β по теореме 2.3 через точку а можно провести прямую с 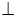а. Прямые в и с по построению имеют только одну общую точку А и обе перпендикулярны

Рис.29

Задача 2. Верхние концы двух вертикально стоящих столбов, удаленных на расстояние3, 4 м, соединены перекладиной. Высота одного столба 5, 8 м, а другого – 3, 9 м. Найдите длину перекладины.

АС = 5, 8м, ВD = 3, 9 м, АВ -? (рис.30)

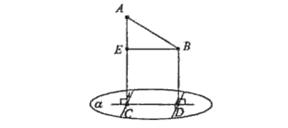
Рис.30

Решение:

АЕ = АС – СЕ = АС – ВD = 5, 8 – 3, 9 = 1, 9 (м)

По теореме Пифагора из ∆ АЕВ получаем:

АВ² = АЕ² + ЕВ² = АЕ² + СD² = ( 1, 9)² + (3, 4)² = 15, 17 (м²)

АВ = 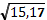= 3, 9 (м)

Задачи

Цель. Учиться анализировать в простейших случаях взаимное расположение объектов в пространстве, использовать при решении стереометрических задач планиметрические факты и методы.

1. Докажите, что через любую точку прямой в пространстве можно провести перпендикулярную ей прямую.

2. Прямые АВ, АС и АD попарно перпендикулярны. Найти отрезок СД, если:

1) АВ = 3см, ВС = 7см, АD = 1, 5 см;

2) ВД = 9 см, АD = 5cм, ВС = 16см;

3) АВ = в, ВС = а, АD =d;

4) ВD = с, ВС = а, АD = d

3. Точка А находится на расстоянии a от вершин равностороннего треугольника со стороной а. Найдите расстояние от точки А до плоскости треугольника.

4. Докажите, что если прямая параллельна плоскости, то все ее точки находятся на одинаковом расстоянии от плоскости.

5. Телефонная проволока длиной 15 м протянута от телефонного столба, где она прикреплена на высоте 8 м от поверхности земли, к дому, где ее прикрепили на высоте 20 м. Найдите расстояние между домом и столбом, полагая, что проволока не провисает.

6. Из точки к плоскости проведены две наклонные, равные 10 см и 17 см. Разность проекций этих наклонных равна 9 см. Найти проекции наклонных.

7. Из точки к плоскости проведены две наклонные, одна из которых на 26 см больше другой. Проекции наклонных равны 12 см и 40 см. Найдите наклонные.

8. Из точки к плоскости проведены две наклонные. Найдите длины наклонных, если они относятся как 1: 2 и проекции наклонных равны 1 см и 7 см.

9. Из точки к плоскости проведены две наклонные, равные 23 см и 33 см. Найдите

расстояние от этой точки до плоскости, если проекции наклонных относятся как 2: 3.

10. Найдите расстояние от середины отрезка АВ до плоскости, не пересекающей этот отрезок, если расстояние от точек а и В до плоскости равны: 1) 3, 2 см и 5, 3 см; 7, 4 см и 6, 1 см; 3) a и в.

11. Решите предыдущую задачу при условии, что отрезок АВ пересекает плоскость.

12. Отрезок длиной 1 м пересекает плоскость, концы его удалены от плоскости на расстояние 0, 5 м и 0, 3 м. Найдите длину проекции отрезка на плоскость..

13. Из точек А и В опущены перпендикуляры на плоскость. Найдите расстояние между точками А и В, если перпендикуляры равны 3 м и 2 м, расстояние между их основаниями равно 2, 4 м, а отрезок АВ не пересекает плоскость.

14. Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если: 1) АС = 6 м, ВD = 7 м, СD = 6 м; 2) АС = 3 м, ВD = 4 м, СD = 12 м; 3) АD = 4 м, ВС = 7 м, СD = 1 м; 4) АD = ВС = 5 м, СD = 1 м; 4) АС = а, ВD = в, СD = с; 5) АD = а, ВС = в, СD = с.

15.Из вершин А и В равностороннего треугольника АВС восставлены перпендикуляры АА₁ и ВВ₁ к плоскости треугольника. Найдите расстояние от вершины С до середины отрезка А₁В₁, если АВ = 2 м, СА₁ = 3 м, СВ₁ = 7 м и отрезок А₁В₁ не пересекает плоскость треугольника

16. Из вершин А и В острых углов прямоугольного треугольника АВС восставлены перпендикуляры АА₁ и ВВ₁ к плоскости треугольника. Найдите расстояние от вершины С до середины отрезка А₁В₁, если А₁С = 4 м, АА₁ = 3 м, СВ₁ = 6 м, ВВ₁ = 2 м и отрезок А₁В₁ не пересекает плоскость треугольника.

Ответы и указания к задачам

2. 1) 6, 5 см; 2) 15 см; 3) (а ² – в ² + d ²), 4) а ² – c² +2 d ². 3. а 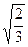. 5. 9м.. Указание к зад.6, 7, 8.Используйте алгебраический метод, ведите переменную х. 6. 6см, 15 см. 7. 15 см, 41 см.8.4 см, 8 см. 9. 9 см. 10. 1) 4, 25 см; 2) 6, 75 см; 3) 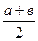11. 1) 1, 05 см; 2) 0, 65 см; 3) 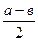12. 0, 6 м. 13 2, 6м. 14. 1) 11 м; 2) 13м; 3) 8м; 4) 7м; 5); 6). 15. 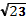м. 16. 7м.