
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Признаки и условия параллельности
|
|
Признаком параллельности прямых является достаточное условие параллельности прямых, то есть, такое условие, выполнение которого гарантирует параллельность прямых.
Целесообразно напомнить несколько вспомогательных определений.
Секущая прямая – это прямая, которая пересекает каждую из двух заданных несовпадающих прямых.
При пересечении двух прямых секущей образуются восемь неразвернутых углов. В формулировке необходимого и достаточного условия параллельности прямых участвуют так называемые накрест лежащие, соответственные и односторонние углы. Покажем их на чертеже (рис.7)
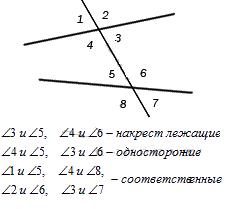
Рис.7
Теорема 2.3. Если две прямые на плоскости пересечены секущей, то для их параллельности необходимо и достаточно, чтобы накрест лежащие углы были равны, или соответственные углы были равны, или сумма односторонних углов равнялась 180 градусам.
Покажем графическую иллюстрацию этого необходимого и достаточного условия параллельности прямых на плоскости (рис.8)

Рис.8
Эти условия можно использовать и в пространстве – главное, чтобы две прямые и секущая лежали в одной плоскости.
Приведем еще несколько теорем, которые часто используются при доказательстве параллельности прямых.
Теорема 2.4. Если две прямые на плоскости перпендикулярны к третьей прямой, то они параллельны.
Существует аналогичная теорема для прямых в пространстве.
Теорема 2.5. Если две прямые в трехмерном пространстве перпендикулярны к одной плоскости, то они параллельны (рис.9)
Рис.9