
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 1. Аксиомы стереометрии
|
|
Стереометрия - это раздел геометрии, в котором изучаются фигуры в пространстве. В стереометрии, так же как и в планиметрии, свойства геометрических фигур устанавливаются путем доказательства соответствующих теорем. При этом отправными являются свойства основных геометрических фигур, выражаемые аксиомами.
Основными фигурами в пространстве являются точка, прямая и плоскость.
Плоскость мы представляем себе, как ровную поверхность крышки стола и поэтому будем изображать ее в виде параллелограмм а.
Плоскость, как и прямая, бесконечна. На рисунке мы изображаем только часть плоскости, но представляем ее неограниченно продолженной во все стороны. Плоскости обозначаются греческими буквами 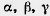
Введение нового геометрического образа — плоскости заставляет расширить систему аксиом. Поэтому мы вводим группу аксиом С, которая выражает основные свойства плоскостей в пространстве. Эта группа состоит из следующих трех аксиом:
С1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
С2. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
Сз. Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
Таким образом, система аксиом стереометрии состоит из аксиом I - IX планиметрии и группы аксиом С.
Замечание. В планиметрии мы имели одну плоскость, на которой располагались все рассматриваемые нами фигуры. В стереометрии много, даже бесконечно много, плоскостей. В связи с этим формулировки некоторых аксиом планиметрии, как аксиом стереометрии, требуют уточнения. Это относится к аксиомам IV, VII, VIII, IX. Приведем эти уточненные формулировки.
IV. Прямая, принадлежащая плоскости, разбивает эту плоскость на две полуплоскости.
VII. От полупрямой на содержащей ее плоскости в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
VIII. Каков бы ни был треугольник, существует равный ему треугольник в данной плоскости в заданном расположении относительно данной полупрямой в этой плоскости.
IX. На плоскости через данную точку, не лежащую на данной прямой, можно провести не более одной прямой, параллельной данной.
Для удобства изложения напомним аксиому I.
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей. Через любые две точки можно провести прямую, и только одну.
Задача 1. Точки А, В, С и D не лежат в одной плоскости. Докажите, что прямые АВ и СD не пересекаются.
Доказательство:
Допустим, что АВ и СД пересекаются, тогда по аксиоме 3 через них можно провести плоскость, и в ней лежат все четыре точки, что противоречит условию задачи. Значит, АВ и СД не пересекаются, что и требовалось доказать.
Задача 2. Можно ли через точку пересечения двух данных прямых провести третью прямую, не лежащую с ними в одной плоскости? Ответ объясните.
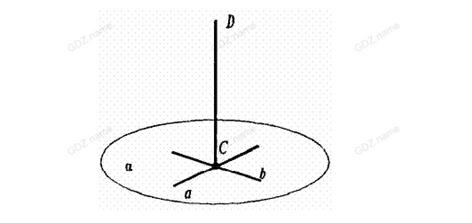
Рис.1
Доказательство:
Можно. Пусть прямые a и b пересекаются в точке С и лежат в плоскости α (аксиома 3, рис.1). Тогда возьмем точку D вне плоскости α (по аксиоме 1) и рассмотрим прямую CD. Это прямая не принадлежит плоскости α, а плоскость, содержащая прямые a и b, единственная (аксиома 3). Значит, прямая CD удовлетворяет условию задачи.
Задачи
Цель. Учиться анализировать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения.
 |
1. Точки А, В, С лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.
2. Даны две непересекающиеся плоскости. Докажите, что прямая, пересекающая одну из данных плоскостей, пересекает и другую.
3. Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.
4. Даны четыре точки, не лежащие в одной плоскости. Сколько можно провести различных плоскостей, проходящих через три из этих точек? Объясните ответ.
5. Можно ли через три точки, лежащие на одной прямой, провести две различные плоскости? Объясните ответ.
Ответы и указания к задачам.
1, 3. Указание. Воспользуйтесь доказательством от противного.
2. Указание. Возьмите точку в другой плоскости и проведите через нее и данную прямую плоскость. Примените к этой плоскости аксиому параллельных.
4. Четыре плоскости.