Свойства параллельных плоскостей

1. Если плоскость пересекает две параллельные плоскости, то прямые пересечения параллельны (рис.15)

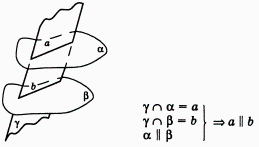
Рис.15

2. Если прямая пересекает одну из параллельных плоскостей, то она пересекает и другую плоскость (рис.16)

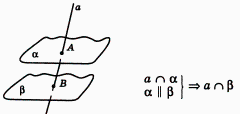
Рис.16

3. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны (рис.17)

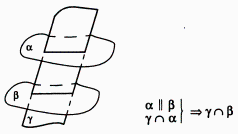
Рис.17

4. Через точку, не лежащую на плоскости, можно провести одну и только одну плоскость, параллельную данной плоскости (рис.18)

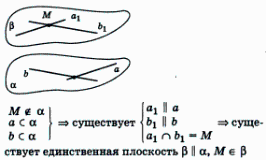
Рис. 18

Задача 1. Докажите, что если прямые АВ и СD скрещиваются, то прямые АС и ВD тоже скрещиваются.

Доказательство:

Если прямые AC и BD не являются скрещивающимися, то они могут быть пересекающимися или параллельными, но в обоих случаях они лежат в одной плоскости α, тогда A α, B ∈ α, С ∈ α, D ∈ α. Таким образом, прямые AB и СD также лежат в одной плоскости, что невозможно по условию, так как AB и CD скрещивающиеся. Значит, AC и BD - скрещивающиеся, что и требовалось доказать.

Задача 2. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А₁, В₁ и М_1. Найдите длину отрезка ММ_1, если отрезок АВ не пересекает плоскость и если:

1) АА₁ =5 м, ВВ₁ = 7м; 2) АА₁ =3, 6 дм, ВВ₁ = 4, 8 дм;

3) АА₁ =8, 3 см, ВВ₁ = 4, 1 см; 4) АА₁ = a, ВВ₁ = в

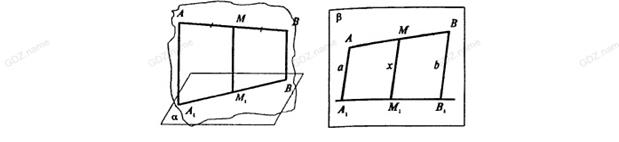
Рис.19

Решение: Прямые АА_1, ММ₁, ВВ₁ лежат в одной плоскости β (рис.19). Значит, точки А₁, В₁и М₁ лежат на прямой А₁В₁пересечении плоскостей α и β. Рассмотрим далее картинку в плоскости β. По теореме Фалеса М₁ середина отрезка А₁В₁А, значит ММ₁-средняя линия трапеции АА₁В₁В и по теореме о средней линии:

ММ₁= 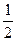(А₁ + ВВ₁). Тогда:

1) ММ₁ = 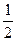(5+7) = 6 (м);

2) ММ₁ = 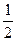(3, 6 +4, 8) = 4, 2 (дм);

3) ММ₁ = 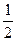(8, 3+4, 1) = 6, 2 (см);

4) ММ₁ = 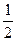(а + в)

ЗАДАЧИ

Цель. Учиться анализировать в простейших случаях взаимное расположение объектов в пространстве, использовать при решении стереометрических задач планиметрические факты и методы.

1.Прямые АВ и СD пересекаются. Могут ли прямые АС и ВD быть скрещивающимися?

2. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А₁, В₁ и М_1. Найдите длину отрезка ММ_1, если отрезок АВ не пересекает плоскость и если:

1) АА₁ =5 м, ВВ₁ = 7м; 2) АА₁ =3, 6 дм, ВВ₁ = 4, 8 дм;

2) АА₁ =8, 3 см, ВВ₁ = 4, 1 см; 4) АА₁ =a, ВВ₁ = в

Решите задачу при условии, что отрезок АВ пересекает плоскость.

3. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пресекающие плоскость в точках В₁ и С₁. Найдите длину отрезка ВВ_1, если: 1) СС₁ = 15 см, АС: ВС = 2: 3; 2) СС₁ = 8, 1 см, АВ: АС = 11: 9; 3) АВ = 6см, АС: СС₁ = 2: 5; 4) АС = а, ВС = в, СС₁ = с

4. Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма

5. Точки А, В, С, D не лежат в одной плоскости. Докажите, что прямая, проходящая через середины отрезков АВ и ВС, параллельна прямой, проходящей через середины отрезков АD и СD.

6.Докажите, что если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую

7.Даны две скрещивающиеся прямые. Как провести через них две параллельные плоскости?

8.Параллелограммы АВСД и АВС₁Д₁ лежат в разных плоскостях. Докажите, что четырехугольник СDD₁С₁ тоже параллелограмм.

9. Через вершины параллелограмма АВСD, лежащего в одной их двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А_1, В_1, С_1, D_1. Докажите, что четырехугольник А₁В₁С₁D₁ тоже параллелограмм.

10.Через вершины треугольника АВС, лежащего в одной из параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А_1, В_1, С_1. Докажите равенство треугольников АВС и А₁В₁С₁.

11. Даны две параллельные плоскости. Через точки А и В одной из этих плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А₁ и В_1. Чему равен отрезок А₁В_1, если АВ = а?

Ответы и указания к задачам

1. Указание. Используйте метод от противного

2.1) 1м; 2) 0, 6 дм; 3) 2, 1 см; 4) 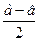. 3.1) 37, 5 см; 2) 9, 9 см; 3) 15 см;

4) с (1 + 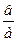). 11. А₁В₁ = а