
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Параллельность плоскостей
|
|
Определение. Две плоскости называются параллельными, если они не имеют общих точек.
Для обозначения параллельности используется символ «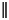 ». Таким образом, если плоскости α и β параллельны, то можно кратко записать α
». Таким образом, если плоскости α и β параллельны, то можно кратко записать α 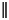 β.
β.
Обычно две параллельные плоскости на чертеже изображаются в виде одинаковых параллелограммов, смещенных относительно друг друга (рис.12)
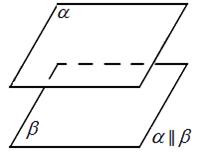
Отметим, что если плоскости α и β параллельны, то также можно сказать, что плоскость α параллельна плоскости β, или плоскостьβ параллельна плоскости α.
Представление о параллельных плоскостях позволяют получить, к примеру, плоскость потолка и пола. Противоположные грани куба лежат в параллельных плоскостях.
При решении геометрических задач часто встает вопрос: «параллельны ли две заданные плоскости»? Для ответа на него существует признак параллельности плоскостей, который представляет собой достаточное условие параллельности плоскостей. Сформулируем его в виде теоремы
Теорема 2.7. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны (рис.13)
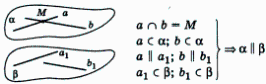
Рис.13
Теорема 2.8. Транзитивность параллельности плоскостей. Если две плоскости параллельны третьей, то они параллельны между собой (рис.14)

Рис.14