
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 5. Угол между образующей цилиндра и диагональю осевого сечения равен φ, Площадь основания цилиндра равна 8
|
|
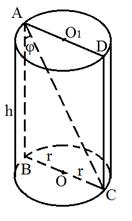 |
Угол между образующей цилиндра и диагональю осевого сечения равен φ, Площадь основания цилиндра равна 8. Найти площадь боковой поверхности цилиндра
Решение. Обозначим на рисунке АВСD - осевое сечение, диагональ осевого сечения – AC, угол CAB=φ. (см. рис. 60).
Рис. 60
Для более удобной подстановки в формулу обозначим, что BC=2r, AB=h.
Из треугольника ABC, 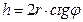 .
.
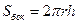 . Вместо h подставляем найденное выражение, получаем:
. Вместо h подставляем найденное выражение, получаем: 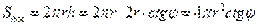 .
.
В полученном выражении π r2=Sосн – по условию. Значит, 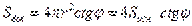 .
.
Ответ: 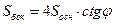 .
.
В данной задаче 3, можно воспользоваться только рисунком 61, не рисуя полностью весь цилиндр.
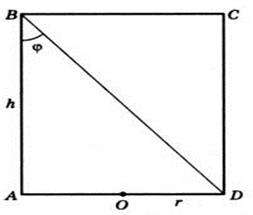
Рис. 61
Задачи
Цель. Учиться изображать цилиндр, его элементы и сечения, выполнять чертежи по условиям задач; решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов), использовать при решении стереометрических задач планиметрические факты и методы.
 |
1. Радиус основания цилиндра 2 м, высота 3 м. Найти диагональ осевого сечения.
2. Осевое сечение цилиндра – квадрат, площадь которого Q. Найти площадь основания.
3. Высота цилиндра 6 см, радиус основания 5 см. Найти площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее.
4. Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найти расстояние этого сечения от оси.
5.  Стороны прямоугольника а и в. Найти боковую поверхность цилиндра, полученного от вращения этого прямоугольника вокруг стороны, равной а.
Стороны прямоугольника а и в. Найти боковую поверхность цилиндра, полученного от вращения этого прямоугольника вокруг стороны, равной а.
6. Диаметр основания цилиндра равен 1, высота равна длине окружности основания. Найти Sбок
7. Высота равностороннего цилиндра равна h. Найти боковую поверхность.
8. Радиус основания цилиндра равен R, боковая поверхность равна сумме площадей оснований. Найти высоту.
9. Площадь осевого сечения цилиндра равна Q. Найти боковую поверхность.
Ответы к задачам
1. 5 м. 2. 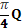 . 3.36 см2 4. 3дм. 5.2π ав 6. π 27. π h2 8. R 9. π Q
. 3.36 см2 4. 3дм. 5.2π ав 6. π 27. π h2 8. R 9. π Q
Конус.
Конусом называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга (Р), - вершины конуса и всех отрезков, соединяющих вершину конуса с точками окружности основания (рис.62)
Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса (РМ). Все образующие конуса равны друг другу.
Поверхность конуса состоит из основания и боковой поверхности
ОР – ось конуса
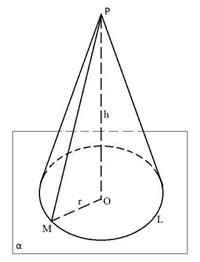 |
Отрезок, заключенный между вершиной и основанием — высотой конуса (РО)
Рис. 62
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. На рисунке изображен конус (рис. 63), полученный вращением прямоугольного треугольника АВС вокруг катета АВ. При этом боковая поверхность конуса образуется вращением гипотенузы АС, а основание — вращением катета ВС.

Рис.63