
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача 3. Решение: Сделаем рисунок и обозначим все данные (рис
|
|
Радиус сферы равен 112 см. Точка, лежащая на плоскости, касательной к сфере, удалена от точки касания на 15 см. Найдите расстояние от этой точки до ближайшей к ней точки сферы.
Решение: Сделаем рисунок и обозначим все данные (рис. 79).

Рис. 79
1) Треугольник OAP – прямоугольный. По теореме Пифагора
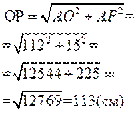
2) 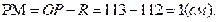
Ответ: 1 см.
Задача 4. Вершины треугольника АВС лежат на сфере, радиус которой равен 13. Найдите расстояние от центра сферы до плоскости треугольника, если АВ = 6, ВС = 8, АС=10 (рис.80)

Рис. 80
Решение. Расстояние от центра сферы до плоскости треугольника – это длина перпендикуляра OK. Точка K располагается именно так, как показано на рисунке, потому что 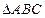 - прямоугольный (проверяется по теореме Пифагора), а AK=KC из равенства треугольников OKC и OKA. Также, если точка K равноудалена от всех вершин треугольника, то она является центром окружности, описанной около этого треугольника. Следовательно, точка K – середина AC,
- прямоугольный (проверяется по теореме Пифагора), а AK=KC из равенства треугольников OKC и OKA. Также, если точка K равноудалена от всех вершин треугольника, то она является центром окружности, описанной около этого треугольника. Следовательно, точка K – середина AC, 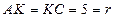 .
.
Рассмотрим треугольник OKC – прямоугольный. По теореме Пифагора, 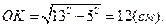
Ответ: 12 см.
ЗАДАЧИ
Цель. Учиться изображать сферу и шар, их элементы и сечения, выполнять чертежи по условиям задач; решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин, использовать при решении стереометрических задач планиметрические факты и методы, использовать приобретенные знания и умения в практической деятельности.
 |
1. Через середину радиуса шара проведена перпендикулярная к нему плоскость. Как относится площадь полученного сечения к площади большого круга?
2. Радиус шара 63 см. Точка находится на касательной плоскости на расстоянии 16 см от точки касания. Найти ее кратчайшее расстояние от поверхности шара.
3. Радиус шара R. Через конец радиуса проведена плоскость под углом 60ок нему. Найти площадь сечения.
4. Радиус земного шара R. Чему равна длина окружности параллельного круга, если его широта равны 60о?
5. Город N находится на 60осеверной широты. Какой путь описывает этот пункт в течение одного часа вследствие вращения Земли вокруг своей оси? Радиус Земли принять равным 6000 км.
Ответы к задачам.
1.3: 4. 2. 4, 8 см.
3. π R2. 4. π R. 5. 785 км