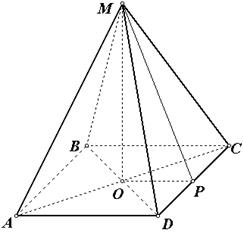
Решение. 1) найдем сторону основания правильной пирамиды по формуле , .

.

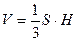1) найдем сторону основания правильной пирамиды по формуле , .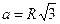

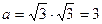2) найдем площадь основания, как площадь правильного треугольника , .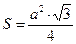

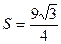Рис.81

3) вычислим объём пирамиды

.

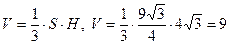Ответ. 9

Задача 2. Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен 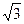, а боковые ребра пирамиды равны 6.(рис.81)

Решение.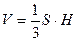

1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. 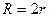, тогда .

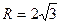2) найдем сторону основания правильной пирамиды по формуле , .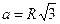

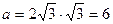3) найдем площадь основания, как площадь правильного треугольника , .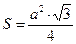

4) из прямоугольного треугольника 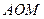по теореме Пифагора находим высоту пирамиды: , .

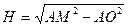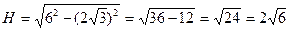5) вычислим объём пирамиды

.

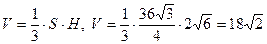Ответ. 18 .

Задача 3. Вычислите площадь боковой поверхности правильной треугольной пирамиды, если радиус описанной около основания окружности равен 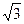, а высота пирамиды равны 1 (рис.82)

Решение.

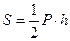
1) найдем сторону основания правильной пирамиды по формуле , .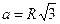

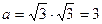2) найдем периметр основания Р = 3· а,

Р = 9.

Рис.82

3) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса

описанной около этого треугольника окружности, т.е. 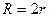, тогда .

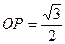4) из прямоугольного треугольника МОР по теореме Пифагора находим апофему МР:

,

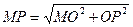МР =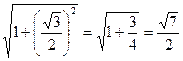

5) вычислим площадь боковой поверхности правильной пирамиды:

, .

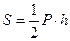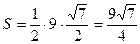Ответ. .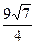

Задача 4. Вычислите объём правильной треугольной пирамиды, сторона основания которой равна 6, а апофема пирамиды равна 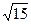(рис.52)

Решение. ,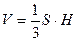

1) найдем радиус описанной около основания и вписанной в основание окружностей: 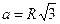, 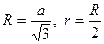то есть .

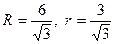2) найдем площадь основания, как площадь правильного треугольника , .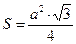

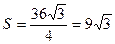3) из прямоугольного треугольника МОР по теореме Пифагора находим высоту: 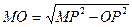, МО = .

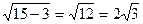4) вычислим объём правильной пирамиды: = .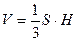

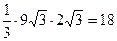Ответ. 18.

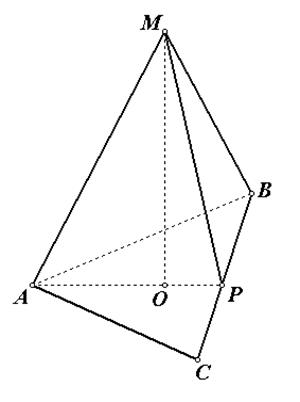
Задача 5.

Вычислите объём правильной треугольной пирамиды, если радиус вписанной в основание окружности равен 2, а высота правильной пирамиды равна 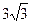(рис.53)

Решение.

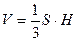
1) радиус вписанной в правильный треугольник окружности в 2 раза меньше радиуса описанной около этого треугольника окружности, т.е. 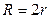, тогда .

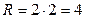2) найдем сторону основания правильной пирамиды по формуле , .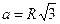

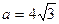3) найдем площадь основания, как площадь правильного треугольника , .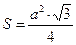

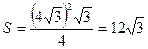4) вычислим объём правильной пирамиды: 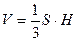= Ответ. 36.

Рис.86

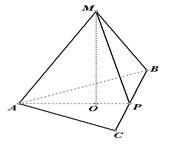
Задача 6. Вычислите площадь боковой поверхности правильной четырехугольной пирамиды, если её ребра равны 5, а радиус окружности, описанной вокруг основания равен 3 (рис.87)

Решение.

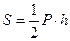
1) найдем сторону основания по формуле 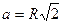, т.е. .

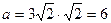2) найдем периметр основания: Р = 4 а,

Р = 24.

3) из прямоугольного треугольника МDР по теореме Пифагора находим апофему МР: 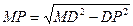, DP = 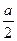Тогда: МР = .

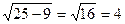Рис.87

4) вычислим площадь боковой поверхности пирамиды: = .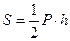

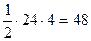Ответ. 48.

Задача 7. В правильной четырехугольной пирамиде площадь боковой поверхности равна 16 а площадь основания 4. Найдите высоту пирамиды (рис.88)