
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. 1) найдем сторону основания: так как в основании пирамиды квадрат с площадью равной 4, то сторона квадрата равна 2
|
|
1) найдем сторону основания: так как в основании пирамиды квадрат с площадью равной 4, то сторона квадрата равна 2, а его периметр 8.
2) по условию 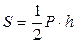 = 16
= 16  т.е.
т.е.
 .
.
Рис.88
3) из прямоугольного треугольника МОР по теореме Пифагора находим высоту: 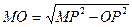 , учитывая, что ОР =
, учитывая, что ОР =  = 1, получаем: МО =
= 1, получаем: МО = 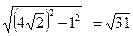 .
.
Ответ. 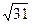 .
.
Задача 8. В правильной шестиугольной пирамиде сторона основания равна 2 
а боковое ребро равно 2 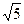 . Найдите объём пирамиды (рис.89)
. Найдите объём пирамиды (рис.89)

Рис.89
Решение.
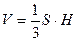
1) найдем площадь правильного шестиугольника по формуле 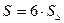 или
или
2) 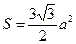 = 12
= 12 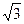 .
.
2) из прямоугольного треугольника МОВ найдем высоту МО, учитывая, что в правильном шестиугольнике  :
: 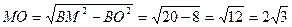 .
.
3) вычисляем объём пирамиды: 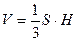 =
= 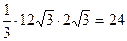 .
.
Ответ: 24.
ЗАДАЧИ
Цель. Учиться решать простейшие стереометрические задачи на нахождение геометрических величин (площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы; проводить доказательные рассуждения в ходе решения задач.
 Объем параллелепипеда, призмы и цилиндра
Объем параллелепипеда, призмы и цилиндра
1. Объем куба 8 м3. Найти его поверхность.
2. Три латунных куба с ребрами 3см, 4 см и 5 см переплавлены в один куб. Какую длину имеет ребро этого куба?
3. Определить объем куба: 1) по его диагонали l; 2) по его поверхности S
4. Кирпич (25 см х12 см х 6, 5 см) весит 3, 51 кг. Найти его плотность.
5. Измерения прямоугольного параллелепипеда 15 м, 50 м и 36 м. Найти ребро равновеликого ему куба.
6. Основанием прямого параллелепипеда служит параллелограмм, у которого одна из диагоналей равна 17 см, а стороны равны 9см и 10 см. Полная поверхность этого параллелепипеда содержит 334 см2.Определить его объем.
7.  В прямом параллелепипеде стороны основания равны 2
В прямом параллелепипеде стороны основания равны 2 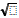 2 см и 5 см и образуют угол в 45о; меньшая диагональ параллелепипеда равна 7 см. Определить объем этого параллелепипеда.
2 см и 5 см и образуют угол в 45о; меньшая диагональ параллелепипеда равна 7 см. Определить объем этого параллелепипеда.
8. По стороне основания а и боковому ребру в определить объем правильной призмы:
1) треугольной; 2) четырехугольной.
9. Найти объем тела, полученного при вращении квадрата вокруг стороны а.
10. Осевое сечение цилиндра - квадрат, диагональ которого равна 4. Найти объем цилиндра.
11.  Боковая поверхность цилиндра равна S, а длина окружности основания C. Найти объем.
Боковая поверхность цилиндра равна S, а длина окружности основания C. Найти объем.
12. Около правильной треугольной призмы описан цилиндр. Высота цилиндра равна 5, а радиус его основания R удовлетворяет уравнению R 2 + R – 6 = 0. Найдите объём призмы.
13.. Около правильной треугольной призмы описан цилиндр. Расстояние между осью цилиндра и стороной основания призмы равно 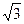 . Высота цилиндра равна трем его радиусам. Найдите объём призмы.
. Высота цилиндра равна трем его радиусам. Найдите объём призмы.
14.. Около правильной треугольной призмы описан цилиндр. Площадь боковой поверхности цилиндра равна 16 p. Найдите объём призмы, если сторона её основания равна
15. Около правильной четырехугольной призмы описан цилиндр, площадь боковой поверхности которого равна 20p. Найдите площадь боковой поверхности призмы.
16.. В правильную четырехугольную призму вписан цилиндр. Объем цилиндра равен 16 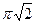 , а радиус окружности, описанной вокруг основания призмы, равен
, а радиус окружности, описанной вокруг основания призмы, равен 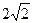 . Найдите диагональ призмы.
. Найдите диагональ призмы.
17. В правильную шестиугольную призму вписан цилиндр. Найдите высоту призмы, если её площадь равна 54 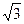 , а радиус цилиндра равен 3.
, а радиус цилиндра равен 3.
18. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 16 p, высота цилиндра равна 4. Найдите объём призмы.
19. Около правильной шестиугольной призмы описан цилиндр. Объём цилиндра равен 10 p. Найдите объём цилиндра, вписанного в эту же призму.
Ответы и указания к задачам
1.24 м2 2. 6 см. 3. 1) l3 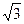 ; 2) S
; 2) S 
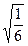 4.1, 8 5. 30 м 6. 360 см37. 60 см3.
4.1, 8 5. 30 м 6. 360 см37. 60 см3.
8.1) а2в 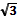 ; 2) а2в 9. π а 3 10. 4π
; 2) а2в 9. π а 3 10. 4π  11.
11. 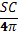
ЗАДАЧИ
Цель. Учиться решать простейшие стереометрические задачи на нахождение геометрических величин (площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы; проводить доказательные рассуждения в ходе решения задач