
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Высота, 2) длительность, 3) громкость, 4) тембр.
|
|
Звук — это объективно существующее в природе физическое явление, вызываемое механическими колебаниями какого-либо упругого тела (туго натянутой струны или мембраны, голосовых связок, металлической или деревянной пластины, воздушного столба, заполняющего корпус духовых инструментов и т.п.), в результате чего образуются звуковые волны, воспринимаемые ухом и преобразуемые в нем в нервные импульсы.
Звуковыми волнами называются периодически чередующиеся сгущения и разрешения в окружающей упругой — например воздушной (то есть газовой) — среде (звукопроводящими средами являются также жидкости и твердые тела), вне которой, как, скажем, в вакууме, звук возникнуть вообще не может. Звуковые волны, распространяющиеся в атмосфере от источника звука равномерно во все стороны (подобно радиоволнам), воспринимаются органами нашего слуха и при помощи определенных участков нервной системы передаются в головной мозг, где и осознаются как конкретные звуки.
В окружающей нас природе существует огромное количество самых разнообразных звуков, которые распадаются на две группы: звуки с определенной высотой (так называемые музыкальные звуки) и с неопределенной высотой (шумы). Музыкальные звуки, имеющие определенную высоту, в отличие от шумовых, обладают еще целым рядом отличительных свойств и составляют основу (то есть звуковой фонд) музыки, использование же шумовых звуков ограничивается лишь эпизодическим применением некоторых из них в отдельных музыкальных произведениях для достижения тех или иных эффектов.
Свойства музыкальных звуков
Любой музыкальный звук имеет четыре основных свойства, которые мы воспринимаем как проявления тех или иных качеств звука:
высота, 2) длительность, 3) громкость, 4) тембр.
Высота звука определяется частотой колебаний звучащего тела и находится от нее в прямой зависимости: чем больше колебаний в единицу времени (за которую принимается секунда) делает источник звука, тем выше будет звук, и наоборот, при уменьшении количества колебаний звук понижается.
В свою очередь, число колебаний в секунду зависит от величины (длины и толщины) и упругости звучащего тела. Возьмем для примера струну. Чем она длиннее (при прочих равных условиях), тем реже ее колебания и, соответственно, тем ниже звук, издаваемый ею. И наоборот, чем струна короче, тем чаще колебания и тем выше звук. Такая же зависимость обычно наблюдается и в отношении поперечного сечения: чем оно больше (толще), тем реже будут производиться колебания и звук, соответственно, понизится, а чем меньше (тоньше) поперечное сечение, тем чаще возникают колебания и звук становится выше. Как видно, в обоих этих случаях обнаруживается обратная зависимость. Что же касается влияния упругости (в данном случае — степени натяжения струны) на высоту звука, то здесь наблюдается прямая зависимость: чем сильнее натянута струна, тем выше звук, и наоборот, чем слабее натяжение, тем звук ниже.
Зависимость между частотой колебаний и высотой звука проявляется не в арифметической, а в геометрической прогрессии. Так, если увеличивать частоту на одну и ту же величину, например на 110 Гц (что практически соответствует укорочению длины струны в два раза), начиная от звука ля большой октавы, имеющего именно это число колебаний в секунду, то в данной последовательности звуков (считая от предшествующего тона) первым будет образовываться интервал чистой октавы, вторым — интервал чистой квинты, третьим — чистой кварты, далее — большой терции, малой терции, еще одной малой терции, а затем — несколько больших секунд и несколько малых. При дальнейшем увеличении частоты колебаний на одну и ту же величину, то есть при дальнейшем укорочении струны будут образовываться еще более узкие интервалы. Этот ряд звуков соответствует натуральному ряду чисел: один, два, три, четыре, пять, шесть и так далее. Именно во столько раз производится увеличение частоты колебаний (укорочение струны) по сравнению с первоначальной, поэтому такой звукоряд носит название натурального звукоряда. Его можно получить, если делить, например, струну на две, три, четыре, пять, шесть и более частей.
Длительностью звука называется выраженное в ритмических единицах время, в течение которого совершаются колебательные движения звучащего тела: чем больше времени продлятся колебания, тем протяженнее будет звук, и наоборот.
Громкость звука находится в прямой зависимости прежде всего от амплитуды колебаний источника звука: чем она больше, тем громче звук, и наоборот, чем меньше амплитуда, тем тише будет звук. Кроме того, на восприятие громкости влияет расстояние от источника звука и отчасти частота колебаний. Так, при одинаковых амплитуде и расстоянии от источника более громкими кажутся звуки среднего регистра.
Иногда громкость называют силой звука, но это неточно, ибо хотя по смыслу эти понятия и близки между собой и даже зависимы друг от друга, однако они отнюдь не адекватны по своему значению. Например, при увеличении объективной силы звука в 100 раз его громкость, то есть восприятие силы звука нашим слухом возрастет лишь в два раза, а тысячекратное увеличение силы звука даст лишь трехкратное увеличение громкости и т.д. Сила звука измеряется в децибелах (дб).
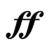
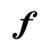
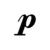
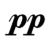 В музыкальной практике громкость звука обозначается различными терминами: громкое звучание — forte (ит. — громко), fortissimo (превосходная степень от forte) и forte fortissimo (еще более громко, чем fortissimo); этому соответствуют знаки f, fff. Аналогично обозначается и тихое звучание— p, pp, ррр (начальные буквы итальянского слова piano— тихо). Количество знаков р также может доходить изредка до четырех, даже пяти. (Обозначение ррррр можно найти, например, в партитуре Шестой симфонии П. Чайковского перед началом разработки первой части.)
В музыкальной практике громкость звука обозначается различными терминами: громкое звучание — forte (ит. — громко), fortissimo (превосходная степень от forte) и forte fortissimo (еще более громко, чем fortissimo); этому соответствуют знаки f, fff. Аналогично обозначается и тихое звучание— p, pp, ррр (начальные буквы итальянского слова piano— тихо). Количество знаков р также может доходить изредка до четырех, даже пяти. (Обозначение ррррр можно найти, например, в партитуре Шестой симфонии П. Чайковского перед началом разработки первой части.)
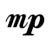
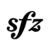
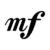 Кроме основных обозначений можно встретить и производные: mf, mp (mezzo forte, mezzo piano), означающие, соответственно, — не очень громко, не очень тихо; sf, sp (subito forte, subito piano), чему соответствует: внезапно громко, внезапно тихо.
Кроме основных обозначений можно встретить и производные: mf, mp (mezzo forte, mezzo piano), означающие, соответственно, — не очень громко, не очень тихо; sf, sp (subito forte, subito piano), чему соответствует: внезапно громко, внезапно тихо.

 Для обозначения постепенного нарастания или ослабления звучания используются термины crescendo и diminuendo, заменяемые часто «вилками». Иногда к словам crescendo и diminuendo добавляется обозначение росо а росо, что означает — постепенно, понемногу.
Для обозначения постепенного нарастания или ослабления звучания используются термины crescendo и diminuendo, заменяемые часто «вилками». Иногда к словам crescendo и diminuendo добавляется обозначение росо а росо, что означает — постепенно, понемногу.
Тембром называется характер звучания, или окраска звука. Тембр зависит от многих причин, как объективного, так и субъективного свойства: конструкции инструмента, материала, из которого он сделан, и его качества (например, сорта дерева, состава металлического сплава и т. п.), способа звукоизвлечения и мастерства исполнителя, среды, в которой распространяется звук, и расстояния от его источника. Но особенно большое значение для формирования тембра музыкальных звуков имеет натуральный звукоряд.
Известно, что каждый звук является сложным, то есть состоит из нескольких одновременно звучащих тонов. (В этом смысле звук можно сравнить с лучом света, который, преломляясь при прохождении через прозрачную призму, разлагается на различные цветовые полосы, образующие спектр, состоящий из семи видимых цветов радуги: красно-оранжевого, желтого, зеленого, голубого, синего и фиолетового). Звучащая струна, например, делится одновременно на свои половины, трети, четверти, пятые, шестые части и так далее, которые будут колебаться самостоятельно.
Человек слышит один звук, обладающий определенной высотой, соответствующей частоте колебаний целой струны. Частоты же колебаний частей струны, издающих так называемые частичные тоны, не воспринимаются слухом как отдельные самостоятельные звуки. Тоны, соответствующие этим частотам, сливаются с основным, придавая звуку определенный колорит.
Тоны, входящие в состав сложного звука, принято называть гармоническими составляющими тонами или просто гармониками. Первый из них, возникающий от колебаний всей струны, называется основным тоном (что соответствует первому частичному тону), следующие далее называются обертонами, то есть тонами, лежащими выше основного.
Частичные тоны
Частичные тоны или обертоны (от нем. Oberton - верхний тон) - это неизбежные примеси, присутствующие в звуке любой природы. Их частоты всегда кратны частоте основного звука, а их количество и громкость может сильно варьироваться, благодаря чему и образуется различная тембровая окраска звука.
Если бы струна воспроизводила только основной тон, то форма ее волны соответствовала бы следующему графическому изображению:
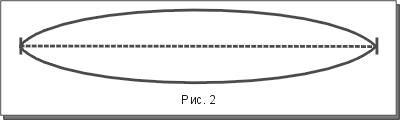
Но звуковая волна на практике всегда имеет довольно сложную форму, часто далеко не походящую на математическую синусоиду. Происходит это вследствие того, что колеблющееся тело (в нашем случае струна), вибрируя, преломляется в равных частях. Эти части производят самостоятельные колебания в общем процессе вибрации тела и образуют дополнительные волны, соответствующие их длине. Дополнительные (простые) колебания и вызывают образование частичных тонов.
Высота частичных тонов различна, так как скорость колебания волн, от которых они образуются, не одинакова. Например, длина волны второго частичного тона, образующейся от половины струны, в два раза короче волны основного тона, а частота колебаний ее в два раза скорее и т. д.:
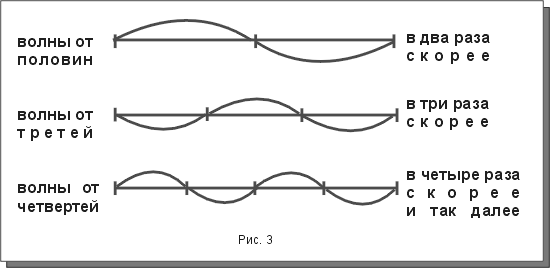
Если принять за единицу число колебаний первого звука (основного тона) струны, то числа колебаний частичных тонов выразятся рядом целых чисел. Такой ряд звуков называется натуральным звукорядом. А обертоны, кратные основному тону по целому числу называются гармониками.
Приняв за основной тон звук до большой октавы, мы будем иметь следующий ряд звуков:

Пример гармонических обертонов: (абсолютная гармония)
| f | 440 Hz | основной тон | первая гармоника |
| 2f | 880 Hz | первый обертон | вторая гармоника |
| 3f | 1320 Hz | второй обертон | третья гармоника |
| 4f | 1760 Hz | третий обертон | четвертая гармоника |
Но в звуке струны имеются не только гармонические обертоны. Дело в том, что реальная, а не идеальная струна, может иметь утолщение или утоньшение на каком-то участке (либо производственный деффект, либо дефект от долгой игры на струне, от грязи, ржавчины и бог знает чего еще). Следовательно этот участок будет производить обертоны немного отличающиеся от идеальной гармоники. Такие обертоны называются ингармониками. Звуковая волна ингармоники не всегда бывает идеально периодичной.
Не всегда наличие ингармоник является недостатком. В некоторых случаях способность музыкальных инструментов (барабанов, там-тамов, колокольчиков) производить обертоны, которые немного ниже или выше значения кратного основному тону, ценятся именно за это уникальное звучание. Заметим, что некоторые инструменты, например, камертон или флейта, способны выдавать чистый или практически чистый, идеальный звук, так как их обертоны находятся очень близко к кратному основному тону, т.е. ингармоники отсутствуют или неуловимы.
Столь сложная структура звучания простой одиночной струны не воспринимается нами сознательно, потому что подобное строение имеют, в принципе, все звуки, с которыми мы имеем дело в своей жизни; а также потому, что громкости, амплитуды этих призвуков чаще всего на несколько порядков меньше, чем амплитуда главной, основной частоты струны.
На характер тембра влияют и количество слышимых обертонов,, и то или иное распределение громкости между отдельными гармониками сложного музыкального звука. Если, например, вторая гармоника будет громче основного тона, третья — громче второй, а затем громкость будет снижаться, то возникнет тембр, близкий тембру гобоя. На некоторых электрических музыкальных инструментах можно подобрать любую интенсивность различных обертонов и, составляя, таким образом, из отдельных простых тонов сложный звук, имитировать тембры различных музыкальных инструментов. Так, например, если выделить нечетные гармонические тоны — первый, третий и пятый, — то в результате синтезируется тембр кларнета.
Музыкальный строй.
Строем называется система организации музыкальных звуков по высоте, выраженная в соотношениях частот их колебаний. Любой строй отталкивается от точно определенной высоты какого-либо одного звука. В большинстве случаев таким звуком-ориентиром служит ля (а) первой октавы, частота колебаний которого в настоящее время установлена в 440 Гц (при температуре воздуха 20°С). Именно эта высота данного звука и является международным эталоном, по которому производится настройка всех музыкальных инструментов, а также определяется высота и остальных звуков музыкальной системы.
Музыкальные строи: Пифагоров, Чистый, Темперированный
Начать историю о проникновении математики в музыку (и наоборот) следует, вероятно, с рассказа о находках древнегреческих учёных. Находки эти касались, главным образом, высотных соотношений между различными нотами музыкальной гаммы. Соотношения эти связываются обычно с именем Пифагора, однако ещё до его трудов людям, конечно, было известно о существовании так называемых натуральных флажолетов.
Речь идёт вот о чём: если на струнном инструменте одновременно с защипыванием струны пальцем или плектром (или возбуждении её смычком) коснуться её середины, будет слышна не основная нота, а нота, на октаву более высокая. У многих народов существовали или существуют и поныне простейшие струнные инструменты с одной струной. Восходят они, вероятно, ещё к древнейшим «поющим лукам», и, по крайней мере, на заре цивилизации инструменты эти были распространены достаточно повсеместно. Греческий вариант такого однострунного инструмента назывался «монохорд» (что, собственно, и означает ни что иное как «одна струна»).
Естественно, исполнители прекрасно знали о возможностях своего инструмента – о том, что из монохорда можно извлечь не один звук, а целый их набор. Звук будут изменяться в зависимости от того, в какой именно точке исполнитель коснётся струны пальцем. Для тех, кто не имел в своей житейской практике дела с натуральными флажолетами, следует отдельно отметить: речь здесь идёт не о фактическом «укорочении струны», какое имеет, например, место при игре на гитаре, когда часть струны ниже пальцев левой руки музыканта оказывается прижата к грифу и не участвует в образовании звука. В случае с монохордом звучит по-прежнему вся струна, полной своей длиной, однако прикосновение пальцем в определённой точке вызывает гашение колебаний в этой конкретной точке. Коснувшись середины струны, вы остановите наиболее низкие, редкие её колебания, сопровождающиеся смещением средней точки относительно оси струны. Однако более частые колебания половинок струны, при которых средняя точка остаётся на месте, а струна изгибается наподобие латинской буквы S, при этом не прекратятся.
Прикосновение к струне в её центре (когда точка прикосновения делит струну на 2 равные части) приводит к повышению звука на октаву. Если же делить струну на неравные, но кратные части можно получить и другие звуки. Так, разделив струну в отношении 1: 2 (то есть, прикоснувшись к ней на расстоянии 1/3 её длины от её начала) можно вызвать звук, на дуодециму (квинту через октаву) - более высокий, чем исходный. Отношение 1: 3 приведёт к появлению звука, на две октавы более высокого, чем исходный, а отношение 1: 4 вызовет звук, примерно соответствующий большой терции, взятой через 2 октавы от исходного. Дальнейшее смещение пальца к началу струны, по мере прохождения им кратных соотношений длины, будет приводить к появлению всё более новых звуков. Звукоряд, возникающий при таком древнейшем методе игры, называется обычно естественным звукорядом.
Чтобы рассказанное не казалось экзотикой, имеет смысл упомянуть, что натуральные флажолеты (или обертоны) вовсе не являются прерогативой одних только «поющих луков» и монохордов. Они не только используются в исполнительской практике (например, в виртуозных произведениях для скрипки или гитары), но и являются единственным музыкальным «языком» таких колоритных инструментов как варган, горн (фанфара), а также техники восточного горлового пения.
Однако в течение некоторого (неопределённого и неизвестного нам времени) случайно обнаруженные в незапамятные времена соотношения деления струны на монохорде и высоты звука не были востребованы ни в исполнительской практике, ни в практике создания музыкальных инструментов. Исполнители и музыкальные мастера на протяжении долгого времени действовали интуитивно. Создание флейт и арф возможно и без точного знания параметров настройки инструмента, – и отверстия в тростниковой палочке или кости, и натяжение струн на основании можно подбирать по слуху, постепенно, отталкиваясь от каких-то внутренних представлений о необходимом звучании инструмента.
Но музыкальная культура не стояла на месте, – инструменты постепенно усложнялись и становились совершеннее, совершенствовалась и практика ансамблевого исполнения, – и потому всё более актуальным становился вопрос о настройке инструментов. Об их «настраивании» в пределах ансамбля.
В своих работах Пифагор подытожил следующие известные факты и свои наблюдения:
- Наиболее сложные использовавшиеся в то время в Греции лады (гаммы) состояли из 7 нот.
- Двигаясь по квинтам от исходной ноты наверх и возвращаясь по октавам вниз (в исходную октаву) можно получить (и даже с избытком) все ноты этих гамм.
- Отношение длин частей струны (при её зажатии пальцем), необходимое для повышения звука на квинту составляет 2: 3.
Из этих трёх утверждений следует простой вывод: имея в распоряжении способ построения чистых квинт можно получить полный звукоряд от любого наперёд заданного звука. Такой строй (звукоряд) называется пифагоровым строем.
Пифагоров строй даёт возможность построения полного звукоряда от любой заданной ноты, что, конечно, исключительно важно для совместной игры различных музыкантов. Однако он обладает одним существенным (если не катастрофическим) недостаткам. Пифагоров строй в некотором смысле незамкнут. С теоретической точки зрения это означает, что полутон «до-до#» (хроматический полутон) в пифагоровом строе больше полутона «до#-ре» (диатонический полутон) на величину 243/256-2048/2187, которая называется пифагоровой коммой. На практике же это означает, что музыкант фактически должен заранее «просчитать», какие именно ноты и в каком именно «качестве» он будет использовать при игре, так как от этого будет зависеть конкретная настройка его инструмента.
Настройка инструментов по пифагорову строю весьма проста на практике, однако уже первые попытки игры на «пифагоровых» органах показали, что «враг подкрался с неожиданной стороны» и проблема ещё более зловеща, чем можно было предположить. Большая терция «пифагоровых» органов слишком «остра», напряжённа, и непригодна потому для использования в качестве терции мажорного трезвучия. Вероятно, первыми это заметили певцы хора, которые придерживались «интуитивной», чистой терции с её соотношением частот звуков 5: 4. Причину напряженности пифагоровой большой терции найти не трудно. В пифагоровом строе большая терция получается посредством четырех ходов по чистым квинтам вверх и выражается отношением 64/81, что, конечно, неравно 4/5. Разница между чистой и пифагоровой большими терциями называется дидимовой коммой.
Итак, музыкальная практика и тяга ко всё более сложным гармоническим построениям пришли в противоречие с практикой создания и настройки музыкальных инструментов. Выход был, конечно, быстро найден, однако выход этот трудно назвать удовлетворительным. Чистая терция была введена в арсенал средств для «построения новых нот звукоряда» наряду с использовавшимися в пифагоровом варианте квинтой и октавой. Получившийся строй был назван «чистым». Разработку чистого строя обычно связывают с именем итальянского композитора и музыкального теоретика Джозеффе Царлино (1517-1590).
Чистый строй впервые позволил использовать мажорные и минорные гармонические аккорды (трезвучия) при игре на инструментах с фиксированной частотой звуков. В некотором смысле (хотя и с большими оговорками) Джозеффе Царлино можно даже называть «изобретателем» если не мажорного, то, по крайней мере, минорного аккорда.