Розділення складних спектрів на елементарні смуги

Лабораторна робота ВИКОРИСТАННЯ МЕТОДУ АЛЕНЦЕВА-ФОКА ДЛЯ АНАЛІЗУ КРИВИХ ТЕРМОСТИМУЛЬОВАНОЇ ПРОВІДНОСТІ ТВЕРДИХ ТІЛ

Мета роботи: навчитись використовувати метод Аленцева-Фока для роздiлення кривих термостимульваної провідностії на елементарнi складовi.

Література:

1. Фок М.В. Разложение сложных спектров на индивидуальные полосы при помощи обобщенного метода Аленцева // Тр. ФИАН СССР. – 1972. – т.59. – с.3–24.

2. Сердюк В.В., Ваксман Ю.Ф. Люминесценция полупроводников. – Киев; Одесса: Вища школа, 1988. – 200 с.

Теоретичнi вiдомостi

Розділення складних спектрів на елементарні смуги

Експериментально спостережувані спектри випромінювання часто є неелементарними смугами, а суперпозицією декількох близько розташованих смуг. У таких випадках виникає необхідність розділення складних спектрів на індивідуальні складові. Принцип розділення розглянемо на прикладі найбільш простого випадку, коли складна смуга складається всього з двох елементарних смуг, форма яких описується функціями j₁(l) і j₂(l).

Нехай дві смуги перекриваються лише частково, так що на краях складного спектра є області, де сумарна смуга визначається однією з елементарних (рис.4, а). Така обставина є обов’язковою для застосування цього методу.

Складний спектр вимірюється за двох різних умов, наприклад, коли різні інтенсивності або довжини хвиль збуджуючого світла. При цьому зміна умов повинна впливати лише на відносне вкладання смуг у загальний спектр, не змінюючи їх форми. З цієї причини не рекомендується змінювати температуру.

Тоді складні спектри в цих випадках (рис.4, а і б) описуються функціями:

f₁(l)=j₁(l)+j₂(l), (4.1)

f₂(l)=a₁j₁(l)+a₂j₂(l), (4.2)

де a₁ і a₂ - сталі коефіцієнти.

Залежність відношення f₂/f₁ від l має постійні ділянки (рис.4, в) на краях складної смуги, в тих областях, де елементарні смуги не перекриваються. Величини відношення f₂/f₁ на цих ділянках, як видно з виразів (1) і (2), дорівн коефіцієнтам a₁ і a₂. Помноживши смугу f₁(l) на a₂, одержимо:

a₂f₁(l)=a₂j₁(l)+a₂j₂(l). (4.3)

Звідси

f₂(l)-a₂f₁(l)=(a₁-a₂)j₁(l). (4.4)

Результат таких перетворень зображено заштрихованою областю на рис.4, г. Так як коефіцієнти а₁ і а₂ відомі, то з виразу (4) легко визначається j₁(l).

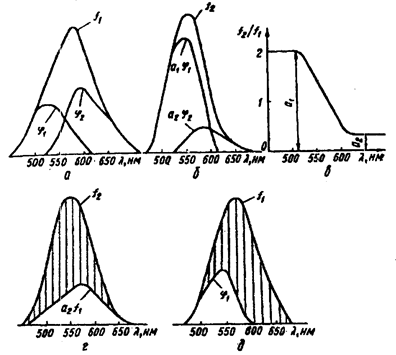
Рис.4.1.

Другу елементарну смугу j₂(l) можна отримати, віднімаючи j₁(l) із сумарного спектра f₁(l), де j₂(l) визначається заштрихованою областю (див.рис.4, д).