
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания по выполнению контрольной работы. В соответствии с учебным планом студенты заочники, обучающиеся по экономическим специальностям, выполнят письменную контрольную работу по курсу «статистика»
|
|
В соответствии с учебным планом студенты заочники, обучающиеся по экономическим специальностям, выполнят письменную контрольную работу по курсу «статистика». Цель- изучить важнейшие методологические вопросы, проверить умение студента применять на практике основные положения курса, приобрести практические навыки в расчетах статистических показателей, построении и оформлении статистических таблиц и графиков, научиться понимать экономический смысл исчисленных показателей, анализировать их.
При выполнении контрольной работы рекомендуется пользоваться следующими учебниками и материалами:
· Н.Н.Ряузов «Общая теория статистики» М.: ФиС, 1984.
· М.Р.Ефимова и др. «Общая теория статистики» М.: ИНФРА-М 1998.
· В.Е.Овсиенко «Сборник задач и упражнений по общей теории статистики» М.: ФиС, 1986,
· конспектами лекций по курсу «статистика» доцента Пчелинцева А.Д.
Задания к контрольной работе составлены в семи вариантах. Выбор варианта зависит от начальной буквы фамилии студента:
| Начальная буква фамилии студента | Номер выполняемого варианта |
| А, Ж, Н, У | первый |
| Б, Я, Ф, П | второй |
| В, И, Э, Х, Ю | третий |
| С, З, И, Ч | четвертый |
| Г, К, Р, Ц | пятый |
| Д, Л, Ш, О | шестой |
| Е, М, Т, Щ | седьмой |
Самовольная замена одного варианта задания другим не разрешается.
Приступая к выполнению контрольной работы, необходимо ознакомиться с соответствующими разделами курса.
Особое внимание нужно обратить на методы построения, технику расчета и экономический смысл статистических показателей.
Далее следует предварительно наметить схему решения каждой задачи, составить макет статистической таблицы, куда будут занесены исчисленные показатели. При составлении аналитической таблицы необходимо дать ей общий заголовок, отражающий краткое содержание таблицы, а также заголовки по строкам и графам, указав при этом единицы измерения, итоговые показатели.
При выполнении контрольной работы необходимо руководствоваться следующими требованиями:
1. Контрольная работа должна быть выполнена и представлена в срок, установленный приказом ректора " Об организации учебного процесса на год".
2. В начале работы должен быть указан номер варианта работы.
3. Задачи нужно решать в том порядке, в каком они даны в задании
4. Перед решением задачи должно быть полностью приведено ее условие. Отделите решение задачи от ее условия некоторым интервалом.
5. Решение задач следует сопровождать необходимыми формулами, развернутыми расчетами и краткими пояснениями. Если имеется несколько методов расчета того или иного показателя, надо применять наиболее простой из них, указав при этом и другие возможные способы решения.
Формулы должны быть приведены в той символике, которая дана в учебниках по «Общей теории статистики» или лекционном курсе.
В процессе решения задач нужно проверять производимые расчеты, пользуясь взаимосвязью между исчисляемыми показателями и обращая внимание на экономическое содержание последних. Задачи, к которым даны ответы без развернутых расчетов, пояснений и кратких выводов, будут считаться нерешенными.
Решение задач следует по возможности оформлять в виде таблиц.
В конце решения каждой задачи необходимо четко сформулировать выводы, раскрывающие экономическое содержание и значение исчисленных показателей.
Все расчеты относительных показателей нужно производить с принятой в статистике точностью до 0, 001, а проценты – до 0, 1.
6. Выполненная контрольная работа должна быть оформлена аккуратно, написана разборчиво, чисто без помарок и зачеркиваний. Запрещается произвольно сокращать слова (допускаются лишь общепринятые сокращения). Все приводимые таблицы надо оформлять в соответствии с правилами, принятыми в статистике.
Страницы работы должны быть пронумерованы и иметь достаточно широкие поля для замечаний рецензента и исправлений (дополнений), вносимых студентом после рецензирования.
7. В конце работы следует привести список использованной литературы (автор, название учебника, главы, параграфа, страницы). Работа должна быть подписана студентом с указанием даты ее выполнения.
8. При удовлетворительном выполнении работа оценивается «допущена к собеседованию». К собеседованию студент обязан учесть все замечания рецензента и, не переписывая работу, внести в нее необходимые исправления и дополнения. После успешного прохождения собеседования студент получает зачет по работе и допускается к экзамену.
Студенты, представившие на проверку неудовлетворительные работы, выполняют работу или заново, или в соответствии с замечаниями рецензента.
Студенты, не получившие зачета по предусмотренным учебным планом письменным работам, к экзамену не допускаются.
Если студент не может самостоятельно выполнить контрольную работу или какую-то ее часть, следует обратиться к лектору за консультацией.
Каждый вариант контрольной работы состоит из 7 задач по наиболее важным разделам общей теории статистики.
Задача 1 составлена на выполнение аналитической группировки статистических данных (См. учебник Ряузова Н. Н. Общая теория статистики.– М.: Финансы и статистика, 1984, с. 86 – 87). (Далее идут ссылки на этот учебник)
Методом аналитической группировки установим наличие связи между среднегодовой стоимостью основных производственных фондов (факторный признак) и стоимостью валовой продукции (результативный признак). Группировка производится по факторному признаку, выделенные группы затем необходимо охарактеризовать приведенными в условии задачи показателями. На первом этапе строим макет групповой аналитической таблицы (с. 118). На втором этапе найдем интервал группировки заводов по среднегодовой стоимости основных производственных фондов и определим группы заводов по факторному признаку (с. 88, 89). Для заполнения макета аналитической таблицы строим рабочую таблицу (с. 119). Данные из рабочей таблицы переносим в макет построенной таблицы и оформляем результаты группировки в виде групповой аналитической таблицы (с. 120). Таблицы должны иметь заглавие, наименование подлежащего и сказуемого таблицы, единицы измерения, расчетные и итоговые показатели и т. д.
Необходимо также дать анализ показателей групповой таблицы и сделать выводы.
Задача 2 составлена на применение средней арифметической и средней гармонической взвешенных. Вид средней выбирается на основе исходной статистической информации и экономического содержания показателя. Например, средняя заработная плата одного рабочего завода определяется отношением фонда заработной платы к числу рабочих. Если в условии задачи по цехам завода имеются данные о заработной плате и численности рабочих, то средняя заработная плата рабочих завода будет исчислена по формуле средней арифметической взвешенной:




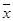 =
= 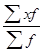 ,
,
гдe 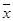 – средняя заработная плата рабочих завода;
– средняя заработная плата рабочих завода;
х – заработная плата рабочего;
 – число рабочих;
– число рабочих;
хf – фонд заработной платы рабочих цела завода.
Если в условии задачи даны показатели заработной платы по цехам завода и фонд заработной платы в цехах завода, то средняя заработная плата рабочих завода будет исчислена по средней гармонической взвешенной:
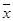 =
= 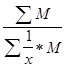 ,
,
где х  – заработная плата рабочих завода;
– заработная плата рабочих завода;
М – фонд заработной платы рабочих каждого завода (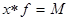 ).
).
Аналогичен подход к расчету других средних показателей: урожайности, цены, себестоимости, выработки продукции, затрат времени, процента выполнения плана и т. д. (с. 163, 164, 171 – 173).
Задача 3. Для решения этой задачи необходимо изучить темы: «Средние величины», «Показатели вариации» и «Выборочное наблюдение».
По имеющимся данным интервального вариационного ряда распределения нужно исчислить среднюю, дисперсию, среднее квадратическое отклонение и коэффициент вариации (с. 165 – 170, 185 – 191). При определении среднего значения признака по группам следует помнить, что величина открытого интервала первой группы приравнивается к величине интервала второй группы, а величина открытого интервала последней группы – к величине интервала предпоследней группы.
Необходимо усвоить существо и практическое применение среднего квадрата отклонений (дисперсии – s 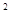 ) и среднего квадратического отклонения (s), который исчисляется как квадратный корень из дисперсии (s =
) и среднего квадратического отклонения (s), который исчисляется как квадратный корень из дисперсии (s = 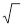 s
s 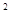 ). Их различие имеет принципиальное значение при определении коэффициента вариации, ошибок выборки и показателей тесноты связи.
). Их различие имеет принципиальное значение при определении коэффициента вариации, ошибок выборки и показателей тесноты связи.
Для расчета ошибок выборки (пункты 4, 5 задачи) надо изучить тему «Выборочное наблюдение», уяснить понятия генеральной и выборочной совокупностей, их характеристики.
Возможная граница генеральной средней определяется:
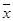 =
= 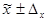




где 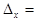 t
t 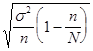 предельная ошибка выборочной средней (для бесповторного отбора).
предельная ошибка выборочной средней (для бесповторного отбора).
Возможная граница генеральной доли определяется:
р= w 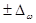 ,
,
где 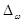 = t
= t 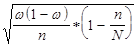 - предельная ошибка выборочной доли (для бесповторного отбора).
- предельная ошибка выборочной доли (для бесповторного отбора).
Задача 4 составлена на расчет и усвоение аналитических показателей динамических рядов. В условии задачи дан интервальный динамический ряд, поэтому средний уровень ряда может быть исчислен только по формуле средней арифметической простой:
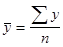 ,
,
т.е. средний уровень ряда равен сумме уровней ряда, деленной на их число.
В зависимости от задачи исследования абсолютные приросты (снижение -Dу), темпы роста (снижение- Т) и темпы прироста (снижение- DТ) могут быть рассчитаны с переменной базой сравнения (цепные) и постоянной базой сравнения (базисные).
Абсолютные приросты:
цепные.........Dу = 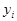
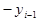
 ,
,
базисные.....Dу =  ,
,
Средний абсолютный прирост исчисляется двумя способами:
1. Как средняя арифметическая простая цепных темпов прироста
D 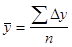 ,
,
2. Делением базисного прироста на число периодов (лет, месяцев и т.д.)
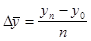 ,
,
темпы роста:
цепные - 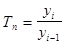 ,
,
базисные - 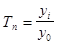 .
.
Среднегодовой темп роста - важнейший показатель развития экономики - исчисляется по формуле средней геометрической двумя способами:
1. 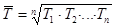 ,
,
где  - цепные коэффициенты роста;
- цепные коэффициенты роста;
n - число коэффициентов;
2. 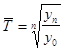 ,
,
где 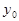 - начальный уровень;
- начальный уровень;
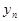 - конечный уровень;
- конечный уровень;
n - число уровней ряда динамики в изучаемом периоде, не считая базисного.
Задача 5 составлена по теме «Индексы» на расчет индекса переменного состава, индекса постоянного состава и индекса, измеряющего влияние структуры на динамику среднего показателя (индексы структурных сдвигов) (стр. 281-284).
Индекс переменного состава равен соотношению средних уровней изучаемого признака. Если, например, изучается динамика средней себестоимости одноименной продукции на двух и более заводах, то индекс себестоимости переменного состава исчисляется по формуле:
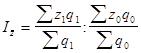 .
.
Изменение средней себестоимости единицы продукции может быть обусловлено изменением себестоимости единицы продукции на каждом заводе и изменением удельного веса производства продукции на заводах.
Выявление влияния каждого из факторов на динамику средней себестоимости продукции можно осуществить при помощи расчета индекса себестоимости постоянного состава и индекса структурных сдвигов.
Индекс себестоимости постоянного (фиксированного) состава или индекс себестоимости в постоянной структуре:
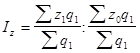 .
.
Этот индекс характеризует изменение средней себестоимости единицы продукции за счет изменения только себестоимости на каждом заводе.
Индекс структурных сдвигов:
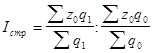 .
.
Этот индекс характеризует изменение средней себестоимости единицы продукции за счет изменения только удельного веса количества произведенной продукции на отдельных предприятиях.
Индекс структурных сдвигов можно исчислить, используя взаимосвязи индексов:
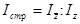 .
.
Задача 6 составлена на расчет среднеарифметического или среднегармонического индексов (стр. 274-278). Практическое их применение зависит от исходной статистической информации. Агрегатный индекс может быть преобразован в среднеарифметический или среднегармонический индекс, при этом должно быть соблюдено тождество между индексами.
Если у исходного агрегатного индекса реальная величина в числителе, то преобразуем в среднегармоническую форму, если реальная величина у исходного агрегатного индекса в знаменателе, то преобразуем в среднеарифметическую форму. Например, индекс цен:
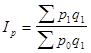 .
.
В числителе индекса реальная величина - фактический товарооборот отчетного периода. Заменив 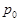 его значением из индивидуального индекса
его значением из индивидуального индекса 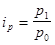 , получим
, получим 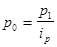 , отсюда
, отсюда
 .
.
Это и есть среднегармонический индекс цен (стр. 276 -278). Преобразование агрегатного индекса цен в среднеарифметическую форму нецелесообразно, практического применения нет.
Агрегатный индекс физического объема товарооборота 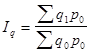 , исходя из правила, будет преобразован в среднеарифметический индекс, т. е.
, исходя из правила, будет преобразован в среднеарифметический индекс, т. е.
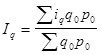 .
.
Задача 7 составлена на измерение взаимосвязи между исследуемыми признаками (факторным и результативным) при помощи эмпирического корреляционного отношения (стр. 310- 312), которое исчисляется по формуле:
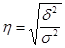 ,
,
где 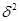 - межгрупповая дисперсия результативного признака (дисперсия групповых средних). Исчисляется она на основе данных аналитической группировки (задача 1) по формуле:
- межгрупповая дисперсия результативного признака (дисперсия групповых средних). Исчисляется она на основе данных аналитической группировки (задача 1) по формуле:
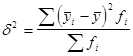 ,
,
где  - групповая средняя результативного признака;
- групповая средняя результативного признака;
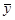 - общая средняя результативного признака;
- общая средняя результативного признака;
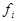 - число заводов в каждой группе.
- число заводов в каждой группе.
Общая дисперсия результативного признака определяется по исходным данным задачи 1 (валовая продукция) по одной из формул:
· 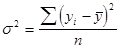 ;
;
· 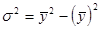 .
.