
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сложные цепи. Метод эквивалентного преобразования схемы
|
|
Метод эквивалентного преобразования схемы используют при расчете простых электрических цепей. В отдельных случаях имеется возможность применить его и для расчета сложных электрических цепей.
Суть метода эквивалентного преобразования схемы заключается в упрощении схемы, когда два (или несколько) однотипных элемента электрической цепи замещаются одним эквивалентным элементом того же типа. Под термином " эквивалентный элемент" подразумевается такой элемент, замещение на который не меняет значений токов и напряжений в остальной части электрической цепи.
Схематичный пример использования метода эквивалентного преобразования схемы для расчета сложной электрической цепи изображен ниже:
Например, после замены источника тока источником напряжения (рис. 1.3) в обобщенной ветви последняя будет выглядеть так:
| = | 
|
| Рис.3.1 | Рис.3.2 |
где 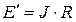 . Обратите внимание, направление эквивалентного источника ЭДС
. Обратите внимание, направление эквивалентного источника ЭДС 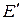 совпадает с напряжением источника тока
совпадает с напряжением источника тока 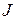 . Ниже будет показано, что данный участок цепи можно упростить, как показано на рис. (3.2), где
. Ниже будет показано, что данный участок цепи можно упростить, как показано на рис. (3.2), где  .
.
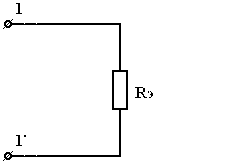
3.2. Последовательное соединение резисторов при эквивалентной замене суммируется:
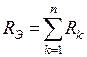 ,
,
где 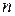 – число последовательно соединенных резисторов. При данном соединении
– число последовательно соединенных резисторов. При данном соединении 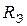 всегда больше большего из
всегда больше большего из 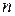 сопротивлений. В частном случае, если каждое из
сопротивлений. В частном случае, если каждое из 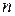 сопротивлений равно
сопротивлений равно 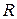 , то
, то 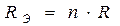 .
.
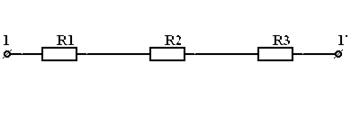
Пример. Определить эквивалентное сопротивление цепи на зажимах  .
.
a)
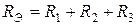 .
.
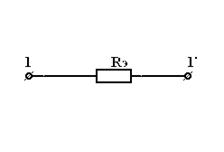
| = | 
|
| Рис 3.4 | Рис 3.5 |
б)
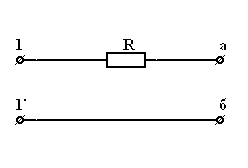
| 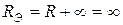 . .
|
| Рис 3.6 |
Здесь 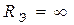 , т.к. разрыв цепи между точками
, т.к. разрыв цепи между точками 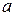 и
и  имеет бесконечно большое сопротивление.
имеет бесконечно большое сопротивление.
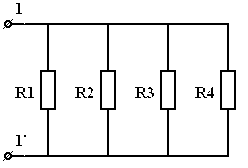
3.3. При параллельном соединении резистора суммируется их проводимость 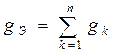 , где
, где 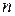 - число параллельно соединенных резисторов,
- число параллельно соединенных резисторов, 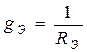 и
и  . При параллельном соединении
. При параллельном соединении 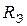 всегда меньше меньшего из
всегда меньше меньшего из 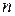 сопротивлений. В частном случае, если каждое из
сопротивлений. В частном случае, если каждое из 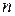 сопротивлений равно
сопротивлений равно 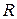 , то
, то 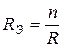 . В случае двух параллельно соединенных сопротивлений
. В случае двух параллельно соединенных сопротивлений  и
и  :
:
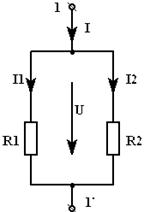
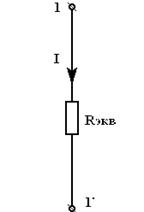
| = | 
|
| Рис 3.7 | Рис 3.8 | |
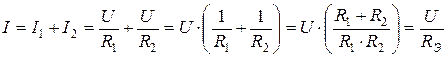 , ,
| ||
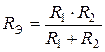
| или | 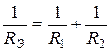 . .
|
Пример. Определить 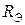 на зажимах
на зажимах 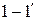 .
.
а)
| = | 
|
| Рис 3.9 | Рис 3.10 |
|
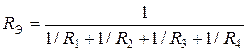 .
.
б)
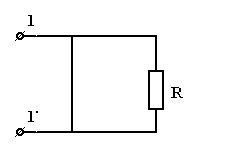
| 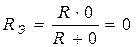 . .
|
| Рис 3.10 |
Здесь 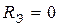 , т.к. сопротивление закоротки равно нулю.
, т.к. сопротивление закоротки равно нулю.
РАСЧЕТНЫЕ ФОРМУЛЫ
| Тип элемента | Последовательное соединение m-элементов | Параллельное соединение m-элементов |
| Резисторы | 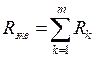
| 
|
| Конденсаторы | 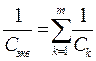
| 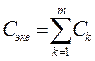
|
| Катушки индуктивности | 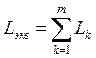
| 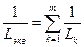
|
3.4. При смешанном соединении резисторов эквивалентное сопротивление 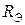 цепи определяет последовательным упрощением схемы и «сворачиванием» ее к одному сопротивлению, равному
цепи определяет последовательным упрощением схемы и «сворачиванием» ее к одному сопротивлению, равному 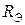 . При расчете токов в отдельных ветвях ЭЦ «разворачивают» в обратной последовательности.
. При расчете токов в отдельных ветвях ЭЦ «разворачивают» в обратной последовательности.
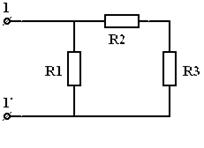
Пример. Определить 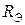 относительно зажимов
относительно зажимов 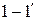 .
.
а)
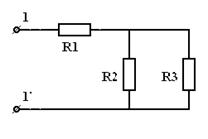
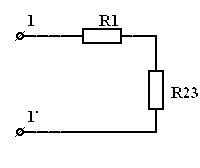
| = | 
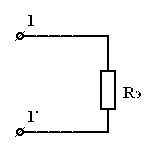
| = | 
|
| Рис 3.11 | Рис 3.12 | Рис 3.12 |
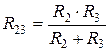 ,
, 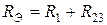
|
.
б)
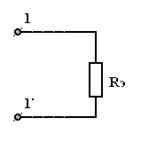
| = | 
| = | 
|
| Рис 3.13 | Рис 3.14 | Рис 3.15 |
|
 ,
, 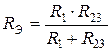 .
.
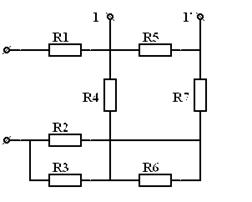
| = | 
|
| Рис 3.16 | Рис 3.17 | |
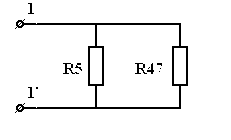
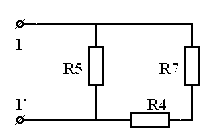
| = | 
|
| Рис 3.18 | Рис 3.19 |
|
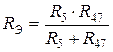 , где
, где 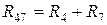 .
.
В последнем примере сопротивление 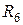 закорочено, а сопротивления
закорочено, а сопротивления 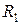 ,
, 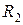 ,
, 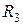 имеют только одну общую точку со схемой и поэтому они не учитываются. Сопротивления
имеют только одну общую точку со схемой и поэтому они не учитываются. Сопротивления 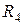 и
и  включены последовательно и эквивалентное им сопротивление
включены последовательно и эквивалентное им сопротивление 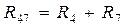 , а
, а 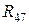 и
и  включены параллельно, поэтому:
включены параллельно, поэтому:
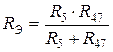 .
.
3.5. Преобразование пассивного треугольника сопротивлений в эквивалентную трехлучевую звезду. Схемы будут эквивалентны, если сопротивления между узлами 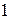 и
и 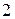 ,
, 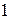 и
и 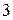 ,
, 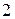 и
и 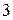 в обеих схемах «звезды» и «треугольника» будут одинаковыми:
в обеих схемах «звезды» и «треугольника» будут одинаковыми:
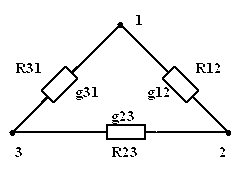
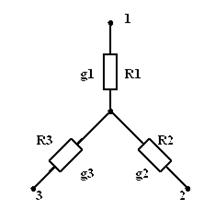
| = | 
|
| Рис. 3.20 | Рис. 3.21 |
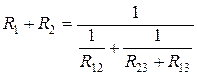 ,
, 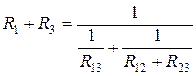 ,
, 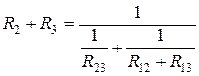 .
.
Решая совместно эти уравнения, получим:
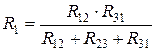 ,
, 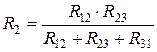 ,
, 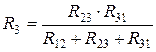 ,
,
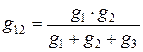 ,
, 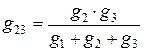 ,
, 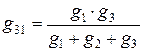 .
.
Обратное преобразование трехлучевой звезды в треугольник:
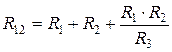 ,
, 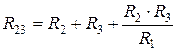 ,
, 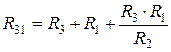 .
.
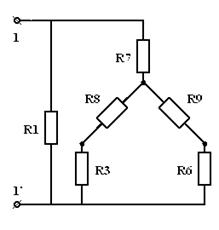
Пример. Определить эквивалентное сопротивление ЭЦ относительно зажимов 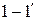 .
.
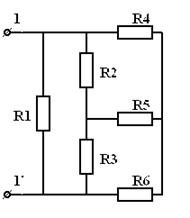
| = | 
|
| Рис 3.22 | Рис 3.23 | |
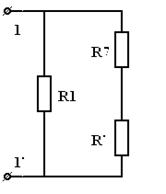
| = | 
|
| Рис 3.24 | Рис 3.25 |
Сначала преобразуем треугольник сопротивлений 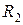 ,
, 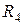 ,
,  в эквивалентную трехлучевую звезду
в эквивалентную трехлучевую звезду  ,
, 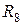 ,
, 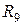 ; затем преобразуем последовательно соединенные резисторы
; затем преобразуем последовательно соединенные резисторы 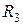 ,
, 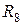 и
и 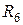 ,
, 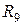 , эквивалентные сопротивления которых соединены между собой параллельно и могут быть заменены одним
, эквивалентные сопротивления которых соединены между собой параллельно и могут быть заменены одним 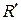 :
:
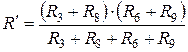 .
.
Резистор 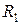 включен параллельно резисторам
включен параллельно резисторам  и
и 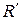 , соединенным между собой последовательно. Поэтому эквивалентное сопротивление всей ЭЦ относительно зажимов
, соединенным между собой последовательно. Поэтому эквивалентное сопротивление всей ЭЦ относительно зажимов 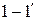 :
:
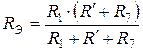 .
.
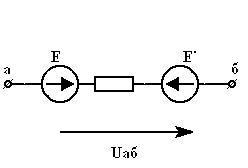
3.6. Преобразование ветвей, содержащих последовательные и параллельные соединения источников ЭДС и тока.
а)
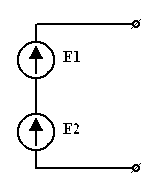
| = | 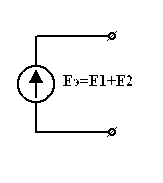
|
| Рис 3.26 | Рис 3.27 |
б)
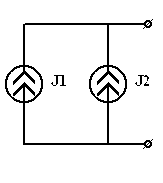
| = | 
|
| Рис 3.28 | Рис 3.29 |
в)
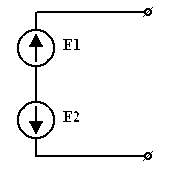
| = | 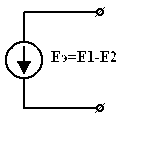
| или | 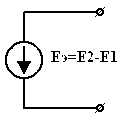
|
| Рис 3.30 | Рис 3.31 | Рис 3.32 |
|
г)
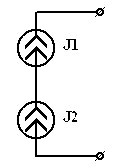
| Если 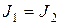 . Два источника тока могут быть соединены последовательно, если они равны и одинаково направлены в противном случае не будет выполняться ЗТК в месте соединения двух источников. . Два источника тока могут быть соединены последовательно, если они равны и одинаково направлены в противном случае не будет выполняться ЗТК в месте соединения двух источников.
|
д)
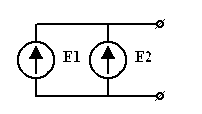
| 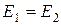 . Два источника ЭДС могут быть включены параллельно, если они равны и имеют одинаково включенную полярность. Если эти условия не выполняются, то ЗНК будет нарушен в контуре, содержащем эти источники. . Два источника ЭДС могут быть включены параллельно, если они равны и имеют одинаково включенную полярность. Если эти условия не выполняются, то ЗНК будет нарушен в контуре, содержащем эти источники.
|
|
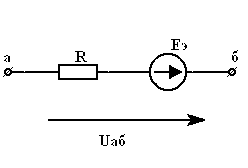
3.7. Часть схемы, состоящей из параллельных ветвей ЭДС 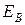 и проводимостями
и проводимостями 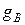 , эквивалентно либо одной ветви с проводимостью
, эквивалентно либо одной ветви с проводимостью 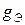 и ЭДС
и ЭДС 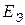 :
:
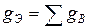 ,
, 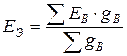 ,
,
либо двум параллельным ветвям с той же проводимостью 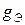 и источником тока
и источником тока 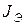 :
:
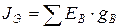 .
.
ПРАВИЛО ЗНАКОВ. Слагаемые 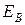 ,
, 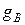 берутся с плюсом при совпадении направления ЭДС
берутся с плюсом при совпадении направления ЭДС 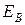 и
и 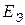 , при несовпадении – с минусом.
, при несовпадении – с минусом.
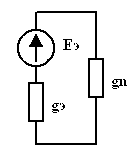
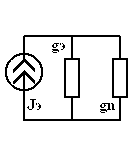
Пример. Преобразовать схему с параллельными ветвями, содержащими источники ЭДС, в эквивалентную.
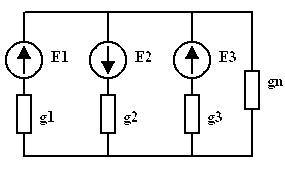
| = | 
| = | 
|
| Рис 3.33 | Рис 3.34 | Рис 3.35 |
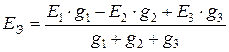 ,
, 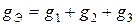 ,
, 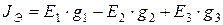 .
.
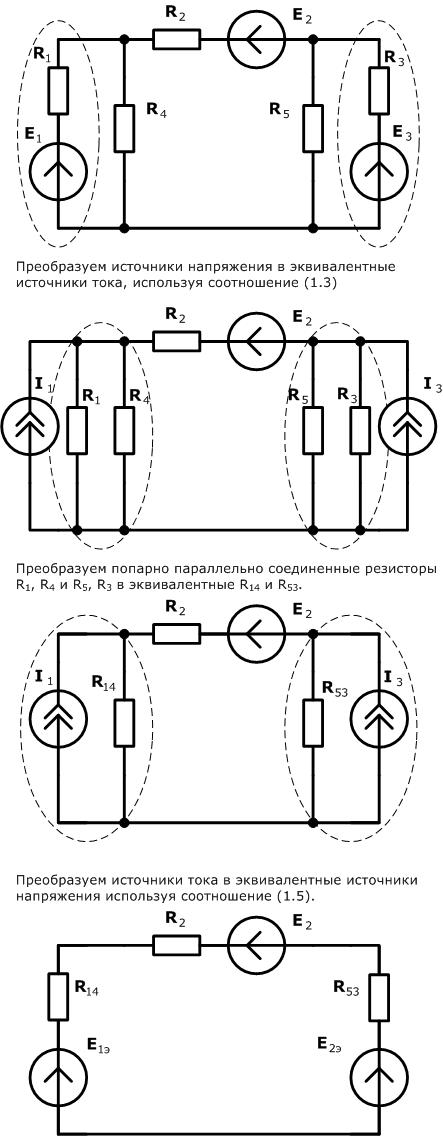
Пример.В заданной ЭЦ (рис.2.1) найти токи, используя эквивалентные преобразования.
Для начала преобразуем источник тока 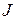 в источник напряжения:
в источник напряжения: 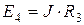 .
.
Заменим сопротивления 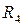 и
и 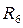 на эквивалентные
на эквивалентные 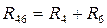 и
и 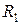 ,
, 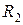 на
на 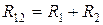 .
.
Элементы 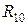 ,
,  ,
, 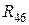 соединены в трехлучевую звезду, которую можно преобразовать в треугольник с сопротивлениями:
соединены в трехлучевую звезду, которую можно преобразовать в треугольник с сопротивлениями: 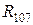 ,
, 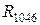 ,
, 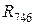 .
.
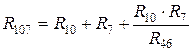 ,
, 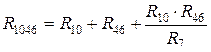 ,
,  .
.
После преобразований схема приобретает вид:
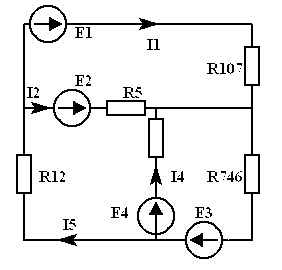
| Þ | 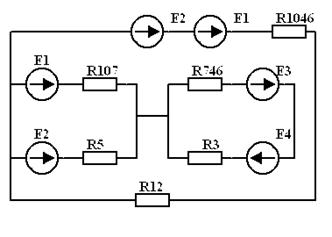
|
Последовательно упрощаем схему,
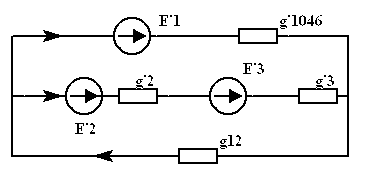
| 
|
где
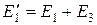 ,
, 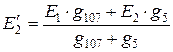 ,
, 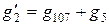 ,
,
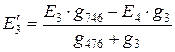 ,
, 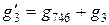 .
.
Схему  можно заменить на
можно заменить на  , где
, где
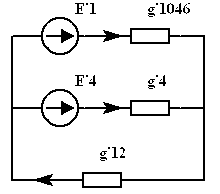
| 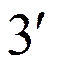
|
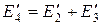 ,
, 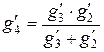 .
.
Заменяя 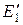 и
и 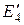 на эквивалентное
на эквивалентное 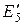 :
:
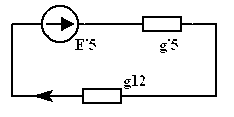
| 
|
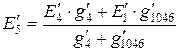 .
.
Тогда ток, протекающий через элементы 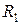 ,
, 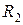 будет равен:
будет равен:
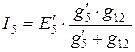 .
.
Токи, протекающие через 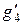 ,
, 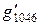 равны: (
равны: (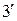 ):
):
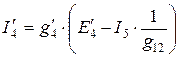 ,
, 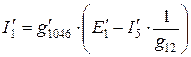 .
.
Посредством 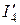 найдем токи на резисторах
найдем токи на резисторах  и
и  (
( и
и 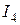 ):
):
1. 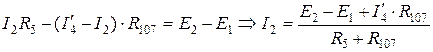 ,
,
1. 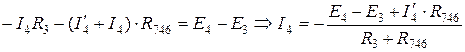 .
.
Остальные токи можно найти посредством ЗТК для изначальной схемы:
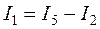 ,
, 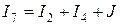 ,
,  .
.