Принцип наложения и метод наложения.

Для линейных электрических цепей справедлив принцип наложения, согласно которому ток (напряжение) любой ветви равен сумме частичных токов (напряжений), создаваемых в этой ветви каждым из источников в отдельности. Этот принцип лежит в основе метода наложения. Метод наложения применим только для расчета линейных цепей.

Частичный ток – ток в ветви от действия только одного источника энергии, когда все остальные источники приняты нулевыми. Пусть в цепи действуют n идеальных источников ЭДС и m идеальных источников тока. Тогда ток в i -ой ветви может быть определен как

.

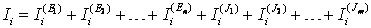Для удобства использования принципа наложения вводят коэффициенты g_ij и k_ij, определяющие связь тока I_i со значениями источников, так как при действии одного источника ток в линейной цепи пропорционален величине источника:

,

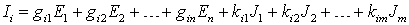где g_ij – взаимная проводимость ветвей i и j (при j = i g_ij = g_ii называют входной проводимостью ветви i), а k_ij – коэффициент передачи по току между ветвями i и j.

Взаимная проводимость (коэффициент передачи по напряжению) g_ij определяется как отношение тока в ветви i, обусловленного действием ЭДС E_j к величине этой ЭДС при условии, что остальные ЭДС и токи источников тока цепи равны нулю: 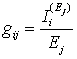. Коэффициент передачи по току k_ij определяется как отношение тока в ветви i, обусловленного действием источника тока J_j к току источника при условии, что остальные источники ЭДС и токи источников тока равны нулю: 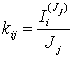. Определить частичные токи и соответственно коэффициенты можно по частичным схемам. Используя расчетные коэффициенты можно решать не только задачи прямого анализа электрических цепей, но и обратные задачи, в которых часть параметров цепи с известной топологией неизвестна и подлежит определению, а в число известных параметров могут быть включены токи и напряжения некоторых ветвей цепи.

Пример 6. Определить ток I ₅, применив метод наложения. Определить значение ЭДС Е ₁, при котором I ₅=0.

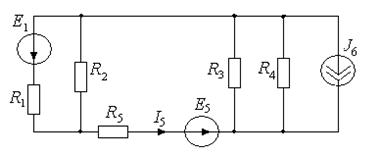
Решение. По методу наложения .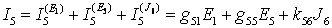

Частичная схема для расчета частичных токов от источника Е ₁ (Е ₅=0, J ₆=0):

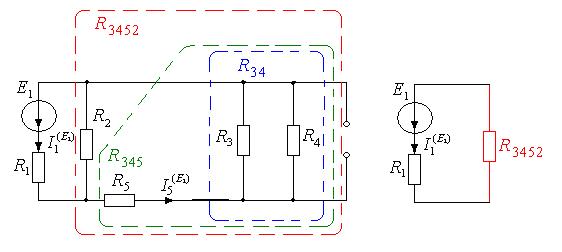
Применим эквивалентные преобразования: 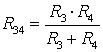(параллельное соединение резисторов), 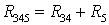(последовательное соединение), 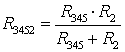(параллельное соединение). Входная проводимость 1-ой ветви , где входное сопротивление 1-ой ветви 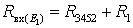. Частичный ток в ветви с источником 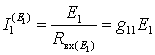. По формуле разброса .

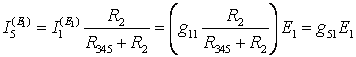Частичная схема для расчета частичных токов от источника Е ₅ (Е ₁=0, J ₆=0):

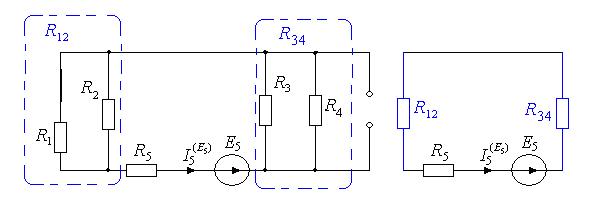
Применим эквивалентные преобразования: , 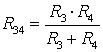(параллельное соединение резисторов). Входная проводимость 5-ой ветви , где входное сопротивление 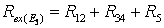, тогда .

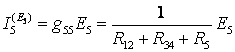Частичная схема для расчета частичных токов от источника J ₆ (Е ₁=0, Е ₅=0):

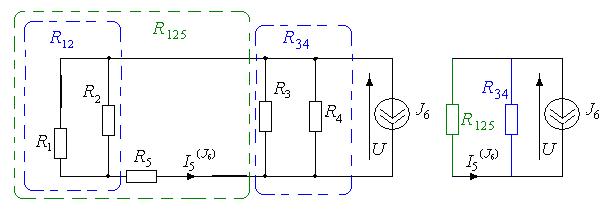
Применим эквивалентные преобразования: , 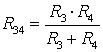(параллельное соединение резисторов), 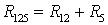(последовательное соединение). Напряжение на источнике тока 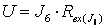, где 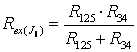, тогда частичный ток .

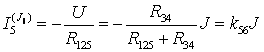Сумма частичных токов: 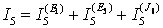, коэффициенты передачи , , .

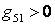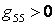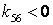Результат наложения частичных токов равен нулю, т.е. 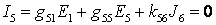, если при неизменности параметров остальных элементов значение ЭДС будет равно .

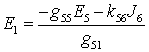9. При расчете электрической цепи методом узловых потенциалов определяются потенциалы узлов цепи, а затем по закону Ома токи в ее ветвях. Метод целесообразно применять в тех случаях, когда число узлов цели меньше или равно числу независимых контуров этой цепи.
Так, для электрической цепи, имеющей четыре узла, составляется три расчетных уравнения (например, для узлов 1, 2 к 3 потенциал узла 4 принимается равным нулю):

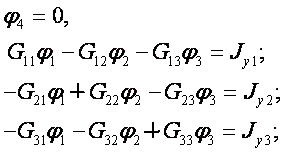
где φ k - искомый потенциал K-го узла цепи (K = 1, 2, 3)
Gkk- (G11, например) собственная (узловая) проводимость k-го узла, равная сумме проводимостей всех ветвей, присоединенных к этому узлу;
Gkm -(G12, например) взаимная (межузловая) проводимость узлов k и m, равная суше проводимостей ветвей, включенных непосредственно между этими узлами;
Jyk (Jy1, например) - узловой ток к-го узла, определяемый из выражения

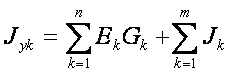
Под знаком первой суммы произведения ЭДС ветвей, присоединенных к К-му узлу, на проводимости этих ветвей учитывается ЭДС с положительным (отрицательным) знаком, если она направлена к К-му узлу (от К-го узла). Под знаком второй суммы со знаком «+» (" -" } учитываются токи источников тока, которые направлены к К-му узлу (от К-го узла).
Если в цепи между двумя узлами включен идеальный источник ЭДС (внутреннее сопротивление которого равно нулю), необходимо принимать равным нулю потенциал одного из его зажимов, тогда потенциал другого зажима источника будет равен ЭДС с
соответствующим знаком, а количество расчетных уравнений сократится.
Последовательность расчета цепи методом узловых, потенциалов рас-
смотрим на примере. Параметры цепи считаются заданными.

ПРИМЕР 1: Определить токи в ветвях цепи (рис. 1) методом
узловых потенциалов. Положительные направления токов принять по рисунку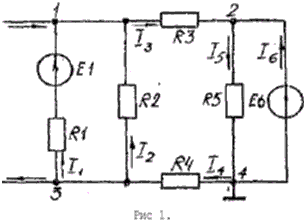

E1=100В R1=10 Ом
E6=200В R2=20 Ом
I=5А R3 =5 Ом R4=25 Ом R5=40 Ом

1. В заданной цепи четыре узла. Приравняем нулю (заземлим) потенциал узла 4.Тогда ф4=0

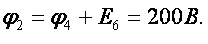
2. Составим расчетную систему уравнений для узлов, потенциалы которых подлежат определению:

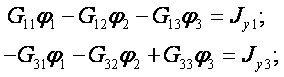
Для узлов 2 и 4 уравнения не составляются, так как потенциалы этих узлов известны.
3. Определим узловые и межузловые проводимости:

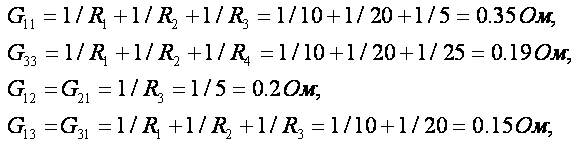
Взаимная проводимость между узлами 2 и 3 равна нулю, так как эти узлы непосредственно не связаны между собой какими-либо ветвями» т.е. G23=G32=0. Проводимость ветви с источником тока J также равна нулю, так как его внутреннее сопротивление бесконечно велико. Если в какой-либо ветви последовательно включено несколько резисторов, вначале определяется общее сопротивление этой ветви, а затем ее проводимость.
Определим узловые токи:

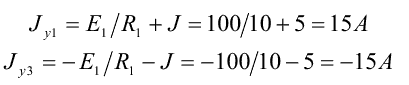
4. Подставим полученные значения узловых и межузловых проводимостей, а также узловых токов в расчетную систему уравнений. Решая ее, определим искомые потенциалы узлов цепи:

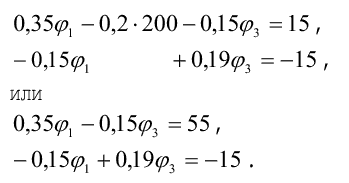
Решить систему уравнений можно методом определителей или с помощью микрокалькулятора по соответствующей программе, однако, если система содержит два уравнения, ее целесообразно решать домножением на общие множители:

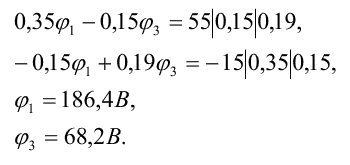
*Запись выше несколько непонятна. Она означает домножение левой и правой частей уравнения на множители. Вообще необходимо любым способом решить систему уравнений: например, подстановкой.

Для проверки расчета целесообразно полученные значения потенциалов, вычисленные с точностью до 3-4 значащей цифры, подставить в исходную систему уравнений, которые при этом, очевидно, должны обратиться в тождества.
5. Используя закон Ома, определим токи в ветвях цепи.
Направления токов в ветвях выбраны произвольно и указаны на схеме (рис. I).
Составим выражение для разности потенциалов (напряжения) между узлами 3 и 1:

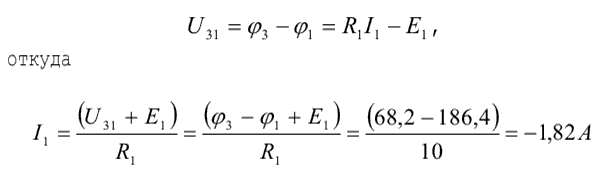
т.е. в дальнейшем при выбранном направлении тока в ветви его величина определяется следующим образом: в числителе выражения от потенциала узла, из которого ток вытекает, вычитается потенциал узла, к которому ток подтекает.
Если в ветви есть ЭДС, она учитывается со знаком «+» (" -"), когда ее направление совпадает (противоположно) с направлением тока, В знаменателе выражения для тока находится суммарное сопротивление ветви. Аналогично определяются токи остальных ветвей:

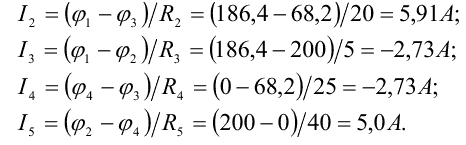
Значения токов I1, I2, и I4 получились со знаком «-». Это свидетельствует о том, что их направления в ветвях противоположны выбранным. Токи I3 и I4 равны между собой в силу принципа непрерывности электрического тока.
Ток в ветви с идеальной ЭДС Е6 определяется из уравнения, составленного по первому закону Кирхгофа. Например, для узла 2

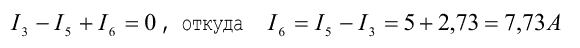
6. Проверка расчета цепи выполняется по законам Кирхгофа
и уравнению энергетического баланса (балансу мощностей),
по первому закону Кирхгофа алгебраическая сумма токов в любом узле электрической цепи равна нулю. Проверяем выполнение этого закона для всех узлов цепи (кроме узла 2: из уравнения для этого узла определялся ток I6:

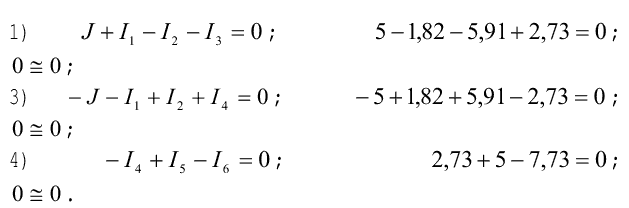
По второму закону Кирхгофа алгебраическая сумма ЭДС в любом замкнутом контуре электрической цепи равна алгебраической сумме падений напряжений на элементах этого контура. Проверяем выполнение этого закона дня всех независимых контуров заданной цепи;
Для контура с элементами Е1, R1 и R2

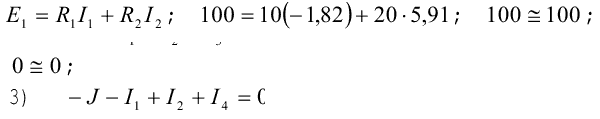
для контура с элементами R2, R3, R4 и R5

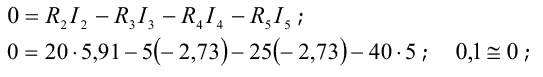
для контура с элементами E1, R3, E6, R4 и R1

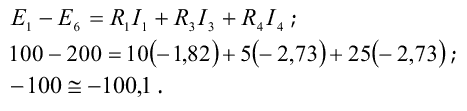
Дня любой электрической цепи мощность, потребляемая резисторами этой цепи, должна равняться мощности источников энергии. Уравнение энергетического баланса (баланс мощностей) в общем виде записывается следующим образом:

В левой части уравнения учтена мощность источников энергии. Мощность источников ЭДС учитывается с положительным (отрицательным) знаком, если ток, протекающий через источник ЭДС, совпадает (противоположен) с направлением ЭДС.
Для определения знака мощности источника тока необходимо определить напряжение на источнике. Если ток источника вытекает из точки с меньшим потенциалом и подтекает к точке с большим потенциалом, мощность источника будет положительной (источник генерирует энергию). Если ток источника вытекает из точки более высокого потенциала по сравнению с потенциалом точки, куда ток втекает, мощность источника будет отрицательной, а режим его работы соответствует потреблению энергии.
В правой части уравнения энергетического баланса записывается арифметическая сумма мощностей, потребляемых резисторами цепи и определяемых по закону Джоуля-Ленца. По своему физическому смыслу эти мощности могут быть только положительными.
Для заданной электрической цепи (рис. I) уравнение энергетического баланса имеет вид

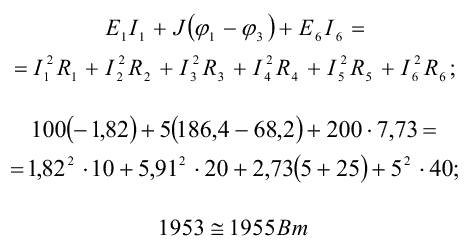
Расчет считается выполненным правильно, если расхождение между левой и правой частями уравнения электрического баланса не превышает 1...2%. Следует помнить, что при выполнении проверки расчета по законам Кирхгофа и балансу мощностей уравнения составляются по выбранным. В начале расчета положительным направлениям токов в ветвях заданной цепи, а числовые значения токов в уравнения подставляются со знаками, полученными в расчете.

10. В тех случаях, когда трехфазная цепь в целом симметрична, а несимметрия носит локальный характер (местное короткое замыкание или обрыв фазы, подключение несимметричной нагрузки), для расчета удобно применять теорему об активном двухполюснике.

При мысленном устранении несимметрии (несимметричного участка) для оставшейся цепи имеет место симметричный режим холостого хода. В соответствии с методом эквивалентного генератора теперь необходимо определить эквивалентные ЭДС и входные сопротивления симметричной цепи. В общем случае – при несимметрии в системе фазных напряжений источника – помимо эквивалентной ЭДС прямой последовательности 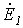будут также иметь место эквивалентные ЭДС обратной 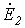и нулевой последовательностей. Однако обычно напряжения генераторов симметричны – тогда 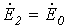. Величина 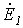, соответствующая напряжению холостого хода 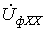на зажимах подключения локальной несимметрии, определяется при отключении локальной несимметричной нагрузки любым известным методом расчета линейных цепей, причем в силу симметрии цепи расчет проводится для одной фазы.

В отдельности рассчитываются входные сопротивления симметричной цепи для различных последовательностей, которая предварительно преобразуется известными методами в пассивную цепь. При этом при расчете входного сопротивления нулевой последовательности 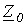необходимо учитывать только те участки цепи, которые соединены с нейтральным проводом или заземленной нейтральной точкой, т.е. принимать во внимание только те ветви, по которым могут протекать токи нулевой последовательности. Схемы для расчета входных сопротивлений прямой и обратной последовательностей одинаковы, однако в случае вращающихся машин величины этих сопротивлений различны.

Поскольку в отдельности для каждой симметричной последовательности имеет место симметричный режим, расчет указанным методом ведется на одну фазу с использованием расчетных схем для прямой (рис. 1, а), обратной (рис. 1, б) и нулевой (рис. 1, в) последовательностей.

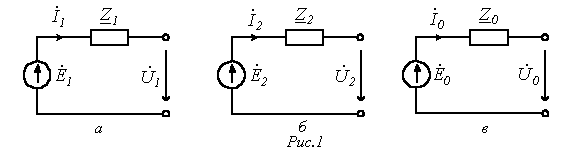
Данным схемам соответствуют соотношения

;

(1)

;

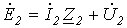(2)

.

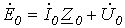(3)

Поскольку соотношений три, а число входящих в них неизвестных шесть 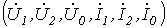, необходимо составление трех дополнительных уравнений, учитывающих конкретный вид несимметрии.

Рассмотрим некоторые типовые примеры применения метода.

Однополюсное короткое замыкание на землю (рис. 2).

.

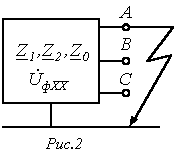
Поскольку фаза А замкнута на землю, то дополнительные уравнения имеют вид

;

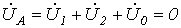(4)

;

.

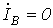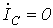Тогда

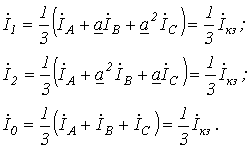
С учетом последних соотношений уравнения (1)…(3) можно записать в виде

;

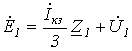(5)

;

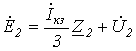(6)

.

(7)

Принимая во внимание (4), а также то, что источник питания симметричный 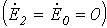, просуммируем (5), (6) и (7):

,

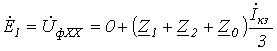откуда получаем

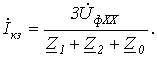
Двухполюсное короткое замыкание без земли (рис. 3).

Для рассматриваемого случая можно записать

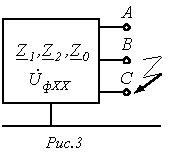
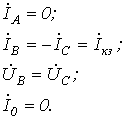
Последнее равенство объясняется отсутствием пути для протекания токов нулевой последовательности.

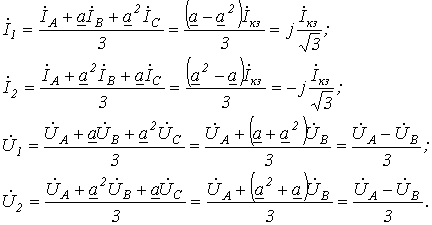
Из двух последних соотношений вытекает, что 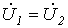. При этом 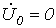, так как 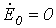и .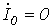

Подставив полученные выражения для напряжений и токов прямой и обратной последовательностей в (1) и (2), запишем

;

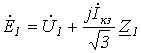(8)

.

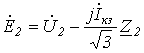(9)

Вычитая из (8) соотношение (9) и учитывая, что в силу симметрии источника 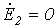, получим

,

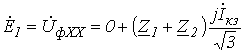откуда

.

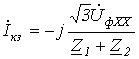Обрыв линейного провода (рис. 4) – определить напряжение в месте разрыва.

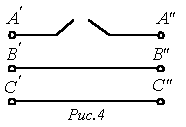В рассматриваемом случае дополнительные уравнения имеют вид

;

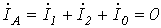(10)

;

(11)

.

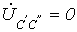(12)

Из соотношений (11) и (12) вытекает равенство:

.

(13)

На основании (1)…(3) с учетом (13) запишем

.

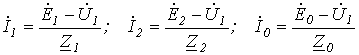Принимая во внимание симметричность источника 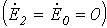, подставим последние выражения в (10):

,

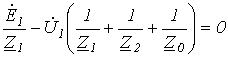- откуда

.

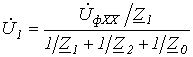Таким образом, искомое напряжение

.

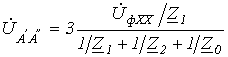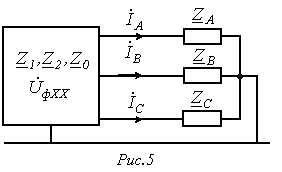Подключение несимметричной нагрузки 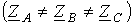к симметричной цепи (рис. 5).

Учитывая, что 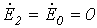, подставим в уравнения (1)…(3) определенные в предыдущей лекции выражения 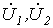и (см. соотношение (12) в лекции №19):

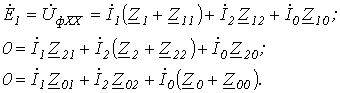
Решая данную систему уравнений, находим 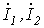и 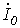. Тогда

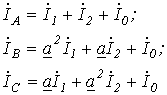
и .

В рассмотренных примерах предполагалось, что необходимые для анализа цепи параметры 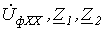и 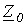предварительно определены. Рассмотрим их расчет на примере предыдущей задачи для некоторой схемы на рис. 6.

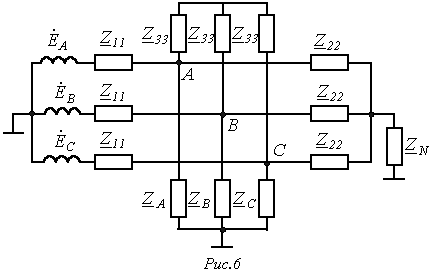
Поскольку при отключении несимметричной нагрузки 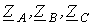оставшаяся часть схемы будет работать в симметричном режиме, для определения 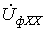получаем расчетную однофазную схему на рис. 7.

Из нее

.

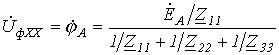Схема для определения входных сопротивлений прямой 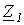и обратной 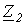последовательностей одна и та же и соответствует цепи на рис. 8, а. В соответствии с ней

.

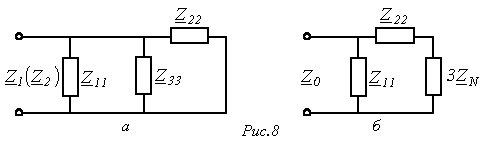
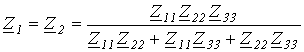Схема для определения 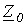, полученная с учетом возможных путей протекания токов нулевой последовательности, приведена на рис. 8, б. Из нее

.

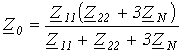11. Передача энергии от активного двухполюсника к пассивному

Для исследования передачи энергии от активного двухполюсника к пассивному вернемся к эквивалентной схеме, показанной на рис. 2.14, д, и будем считать, что rвх - входное сопротивление активного двухполюсника (источника энергии) и Еэк = Uх - эквивалентная ЭДС остаются постоянными, а r - входное сопротивление пассивного двухполюсника может принимать любое значение.
Прежде всего установим соотношение между сопротивлениями rвх и r, при выполнении которого мощность пассивного двухполюсника максимальна.
Мощность пассивного двухполюсника определяется выражениями

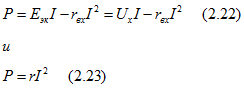
где 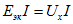-мощность, развиваемая эквивалентным активным двухполюсником; -мощность потерь в этом двухполюснике (в сопротивлении rвх).
Для определения тока I, при котором мощность Р максимальна, найдем производную от Р по I из уравнения (2.22) и приравняем ее нулю:

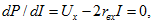
откуда искомый ток 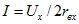[уравнением (2.23) пользоваться нельзя, так как его правая часть содержит две переменные: r и I].
В общем случае (рис. 2.14, д) ток . Значит, мощность максимальна при

т. е. при равенстве входных сопротивлений пассивного и активного двухполюсников.
По (2.23) при r = rв мощность

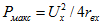
Отношение мощности Р пассивного двухполюсника к мощности 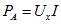, развиваемой эквивалентным активным
двухполюсником, называется КПД эквивалентного активного двухполюсника:

Смотри ещё по разделу на websor:

· Принцип наложения (суперпозиции)

· Свойство взаимности

· Входные и взаимные проводимости, коэффициенты передачи

· Принцип компенсации. Зависимые источники

· Общие замечания о двухполюсниках и многополюсниках

· Линейные соотношения между напряжениями и токами

· Теорема о взаимных приращениях токов и напряжений

· Принцип эквивалентного генератора

· Передача энергии от активного двухполюсника к пассивному

Яндекс.Директ

Размести объявление о вакансиях! Подай бесплатное объявление о вакансии в газету «Только вакансии и резюме»!

Начни зарабатывать в интернетеНачните зарабатывать уже сегодня. Заработок для каждого.

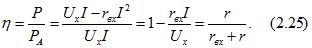
Из (2.25) следует, что при максимальной мощности пассивного двухполюсника КПД равен 0, 5. Более высокие значения КПД будут при .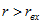
КПД реального активного двухполюсника равен КПД эквивалентного только при выполнении определенного условия. Если при отключении пассивного двухполюсника от реального активного в ветвях последнего не будет токов и потерь, так же как и в эквивалентной схеме на рис. 2.14, д, то КПД реального и эквивалентного активных двухполюсников равны. При невыполнении этого условия КПД реального активного двухполюсника меньше КПД эквивалентного двухполюсника.
Полученные результаты применим, например, для характеристики режима линии передачи электрической энергии небольшой длины, у которой утечкой тока (между проводами) можно пренебречь.

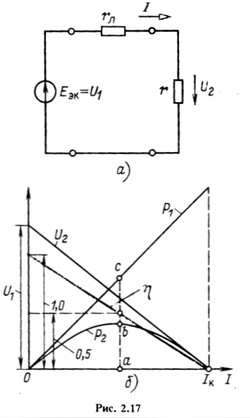
Если в начале линии передачи напряжение U1 поддерживается неизменным (рис. 2.17, а), то линию можно представить в виде последовательного соединения активного двухполюсника с источником ЭДС 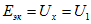(без внутреннего сопротивления), резистивного элемента, учитывающего сопротивление проводов rл, и пассивного двухполюсника - приемника с сопротивлением r (рис. 2.17, а). По (2.22) и (2.25) найдем мощность Р2 приемника и КПД линии передачи:

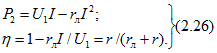
Мощность, развиваемая источником,

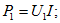
напряжение на выводах приемника

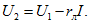
По полученным уравнениям на рис. 2.17, 6 построены зависимости 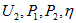от тока I, полностью характеризующие режим линии.
При 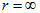(холостой ход линии) ток I = 0 (на рис. 2.17, б -точка в начале координат), при 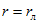ток определяется отрезком Оa и при r = 0 (короткое замыкание линии) значение тока максимально и равно 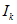. Кроме того, при 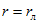мощность 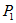, определяемая отрезком ас, равна удвоенной мощности приемника (ас = 2ab = 2bc), и КПД .
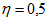По эквивалентной схеме (рис. 2.17, а) установим еще связь между потерями в проводах линии (в сопротивлении rл) и мощностью приемника Р2:

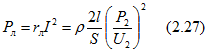
где l - длина линии; S - сечение каждого провода.
Из (2.27), в частности, следует, что при Р2 = const с повышением напряжения U2 требуется меньшее значение тока I и, следовательно, уменьшаются потери в проводах, что в свою очередь позволяет уменьшить сечение проводов. Конечно, при этом надо усилить изоляцию проводов линии.
В случае передачи по линии электрической энергии при большой мощности стремятся получить возможно больший КПД, для чего необходимо, как непосредственно следует из (2.26), иметь 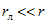. При передаче сигналов по линии связи стремятся получить максимальную мощность в приемнике, что приводит к низкому значению КПД.
Первые опыты передачи электрической энергии при постоянном токе осуществил русский инженер Ф. А. Пироцкий. В 1874 г. вблизи г. Петербурга Ф. А. Пироцкий создал линию передачи энергии при мощности около 6 л. с. на расстояние до 1 км. Затем он проводил опыты передачи электрической энергии по рельсам конно-железной дороги. На основании своих опытов Ф. А. Пироцкий установил, что можно передавать электрическую энергию при большой мощности на большие расстояния. В качестве источников энергии для первичных двигателей он предложил пользоваться энергией водных потоков. Теоретические основы передачи электрической энергии по линии разработал Д. А. Лачинов. В 1880 г. он опубликовал в первом номере журнала " Электричество" свой труд " Электромеханическая работа".
Опыты Ф. А. Пироцкого остались совершенно незамеченными. И лишь этим можно объяснить, что инициатором передачи электрической энергии считался Марсель Депре. В своем докладе в Парижской академии наук (1881 г.) он провозгласил тезис, установленный почти за год до этого Д. А. Лачиновым, а именно: повышая напряжение, можно передавать электрическую энергию при любой мощности на большое расстояние с минимальными потерями (2.27). В следующем году (1882 г.) Депре осуществил на постоянном токе передачу энергии при мощности в 2 л. с. на расстояние 57 км (при напряжении 1500 - 2000 В).