
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Последовательное соединение R, L, С.
|
|
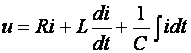
Положим, что в уравнении Кирхгофа (3.4) заданными являются параметры R, L, С и гармоническое напряжение u = Umcos(ω t+ψ) на зажимах цепи, а искомой величиной является ток i.
Ввиду того, что здесь рассматривается установившийся режим цепи гармонического тока, решение этого дифференциального уравнения должно дать гармоническую функцию вида
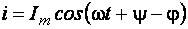 ,
,
где Im и (ψ – φ) – пока неизвестные амплитуда и начальная фаза тока.
Пусть в соответствии с предыдущим параграфом заданное гармоническое напряжение символизируется комплексной функцией 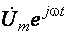 , а искомый гармонический ток – комплексной функцией
, а искомый гармонический ток – комплексной функцией 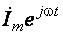 , комплексные амплитуды напряжения и тока равны соответственно:
, комплексные амплитуды напряжения и тока равны соответственно:
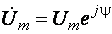 ;
;  .
.
Сложение, дифференцирование и интегрирование гармонических функций в уравнении (3.4) заменяются теми же математическими операциями над действительными частями комплексных функций:
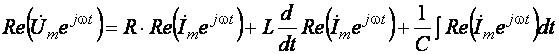 . (3.5)
. (3.5)
Операции над действительными частями комплексных функций могут быть заменены операциями над самими комплексными функциями с последующим выделением действительной части полученного результата. Объясняется это коммутативностью операций сложения, дифференцирования и интегрирования относительно символической операции Re. Итак, (3.5) преобразуется следующим образом:
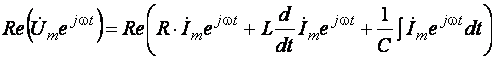 .
.
Полученное уравнение удовлетворяется для любого момента времени. Поэтому заключенные в скобки комплексные выражения, от которых берется действительная часть, должны быть равны друг другу. Производя дифференцирование и интегрирование, получаем:
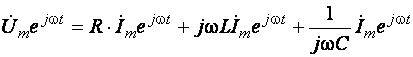 . (3.6)
. (3.6)
Здесь следует обратить внимание на то, что при интегрировании функции еjwt постоянная интегрирования опущена, так как в рассматриваемом установившемся режиме цепи гармонического тока электрические заряды или напряжения на емкостях представляют гармонические функции, не содержащие постоянных слагающих.
В результате сокращения всех частей уравнения (3.6) на множитель еjwt получается алгебраическое комплексное уравнение
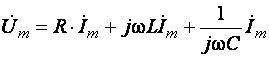 . (3.7)
. (3.7)
Ток Im может быть вынесен за скобки. При этом вводится условное обозначение для комплексного сопротивления рассматриваемой электрической цепи
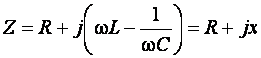 . (3.8)
. (3.8)
Таким образом, получается уравнение
 , (3.9)
, (3.9)
выражающее закон Ома для комплексных амплитуд.
Разделив обе части уравнения (3.9) на 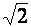 , получим закон Ома для комплексных действующих значений
, получим закон Ома для комплексных действующих значений
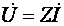 . (3.10)
. (3.10)
Следовательно, комплексное сопротивление электрической цепи равно отношению комплексного напряжения на зажимах данной цепи к комплексному току в этой цепи.
Комплексное сопротивление Z представлено в выражении (3.8) в алгебраической форме. Та же величина в тригонометрической и показательной (полярной) формах имеет вид:
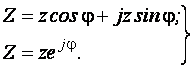 (3.11)
(3.11)
Здесь 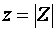 – модуль комплексного числа Z – представляет полное сопротивление цепи, а φ - аргумент комплексного числа Z:
– модуль комплексного числа Z – представляет полное сопротивление цепи, а φ - аргумент комплексного числа Z:
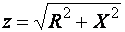 ;
; 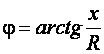 .
.
На основании (3.9) комплексная амплитуда тока
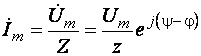 ,
,
где ψ - φ – начальная фаза тока. Следовательно, искомый ток в тригонометрической форме
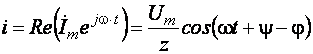 ,
,
что совпадает с результатом, полученным ранее.
На рисунке 3.4 дана геометрическая интерпретация на комплексной плоскости уравнения (3.10). Рисунок 3.4, а относится к случаю, когда реактивное сопротивление цепи имеет индуктивный характер (Х > 0) и соответственно ток отстает по фазе от напряжения (φ > 0). Рисунок 3.4, б относится к случаю, когда реактивное сопротивление цепи имеет емкостный характер (Х < 0), и поэтому ток опережает по фазе напряжение (φ < 0).

а б
Рисунок 3.4 Векторные диаграммы для последовательной цепи R, L, С при х > 0 (а) и x < 0 (б)
В случае чисто реактивной цепи (R = 0) ток отстает от напряжения по фазе на π /2, если сопротивление цепи индуктивное, и опережает напряжение на π /2 при емкостном сопротивлении цепи.
Как видно из векторных диаграмм, приведенных на рисунке 3.4, UR = RI – напряжение на сопротивлении R (совпадает по фазе с током I), UL = jwLI – напряжение на индуктивности L (опережает ток I на угол π /2) и UC = –jI × 1/(wC) – напряжение на емкости С (отстает от тока I на угол π /2).
Геометрическая сумма векторов 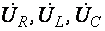 дает вектор приложенного к цепи напряжения
дает вектор приложенного к цепи напряжения
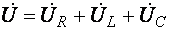 .
.
Активная слагающая напряжения Ua = UR, реактивная слагающая Up = UL + Uc и суммарное напряжение U образуют треугольник напряжений.
Треугольник сопротивлений, подобный треугольнику напряжений и повернутый относительно него на угол ψ - φ (рисунок 3.5), представляет геометрическую интерпретацию уравнений (3.11). Его положение не зависит от начальных фаз 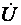 и
и 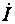 ; сопротивление R откладывается на комплексной плоскости в положительном направлении действительной оси, а реактивное сопротивление х в зависимости от его знака откладывается в положительном (х > 0) или отрицательном (х < 0) направлении мнимой оси (рисунок 3.5, а и б).
; сопротивление R откладывается на комплексной плоскости в положительном направлении действительной оси, а реактивное сопротивление х в зависимости от его знака откладывается в положительном (х > 0) или отрицательном (х < 0) направлении мнимой оси (рисунок 3.5, а и б).
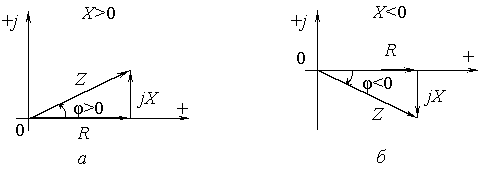
Рисунок 3.5 Треугольник сопротивлений при х > 0 (а) и х < 0 (б)
26. о закону Джоуля — Ленца мощность постоянного тока равна: P = U*I (Вт). (3-4)
Но ведь переменный ток и напряжение меняют величину инаправление. Как же можно подсчитать мощность переменного тока? Изобразим на одном графике синусоиды тока I и напряжения U (рис. 3-5). Для получения кривой, изображающей мощность переменного тока, будем перемножать значения тока и напряжения для различных точек синусоид. В первой половине периода значения тока и напряжения будут положительными, и поэтому произведения их будут также положительными. Будем откладывать их вверх от горизонтальной оси. Во второй половине периода значения тока и напряжения изменят знак на минус. Но так как произведение двух отрицательных величин есть число положительное, то мощность переменного тока за вторую половину периода будет также положительной и изобразится такой же кривой, как и мощность за первую половину периода. Таким образом, мощность остается положительной в течение всего периода. Среднее значение мощности за весь период будет равно произведению действующих значений тока и напряжения. Значит, мощность лампочки не зависит от того, включена ли она в сеть постоянного или переменного тока при одном и том же напряжении. Такое положение справедливо только для цепей без индуктивного сопротивления.
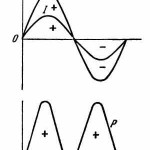
Рис. 3.5. Мощность переменного тока
Как же определить мощность обмотки электромагнита? Здесь придется учитывать индуктивное сопротивление.
Умножив все стороны треугольника сопротивлений (рис. 3-4) на I2, получим новый треугольник, подобный первому, так называемый треугольник мощностей (рис. 3-6). В нем горизонтальный катет выражает знакомую формулу мощности. Действительно, если в формуле мощности (3-4) подставить вместо напряжения U его значение из формулы (3-1) U=I*R, то получим:
P=I2*R. (3-5)
Что же представляют собой две другие стороны треугольника мощностей? Гипотенуза выражает так называемую кажущуюся мощность S, которая выражается в вольт-амперах. Она равна произведению тока на напряжение S = U*I (Вт). Но активная мощность является только составной частью кажущейся мощности. Зная величину кажущейся мощности по показаниям амперметра и вольтметра и значение угла ɸ, можно определить активную мощность, пользуясь тригонометрией. Активная мощность
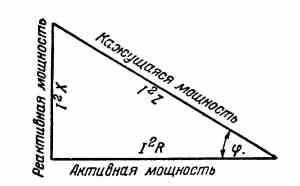
Рис. 3.6. Треугольник мощностей
P = U*I*cosɸ (Вт). (3-6)
Этой формулой можно пользоваться для любых цепей переменного тока. Например, если цепь состоит из активных сопротивлений, то Х=0, а следовательно, по рис. 3-4 угол ɸ также равен нулю. Косинус угла ɸ будет равен единице и активная мощность
P = U*I (Вт).
Таким образом, для цепей, состоящих из активных сопротивлений, мощность равна произведению тока Iна напряжение, как в цепях постоянного тока.
Что же представляет собой вертикальный катет в треугольнике мощностей? Это реактивная или индуктивная мощность. Она не превращается ни в тепло, ни в свет, ни в механическую энергию, а служит в цепях переменного тока для создания магнитного поля.