Пример преобразования

Для электрической цепи необходимо выполнить преобразование треуголькника R12 - R23 - R31 в звезду.

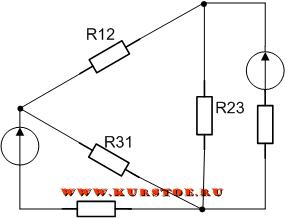
Добавляем к узлам подключения сопротивлений треугольником концы лучей подключения сопротивлений звездой.

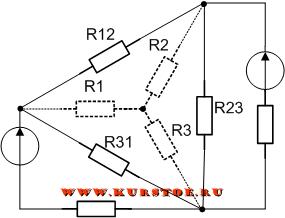
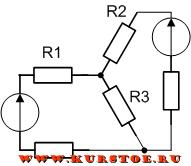
Удаляем соединение сопротивлений треугольником. В результате остается подключение сопротивлений звездой. По формулам рассчитываются значения сопротивлений R1, R2, R3.

13. Простейший генератор переменного тока. Представляет собой проводник вращающийся в постоянном магнитном поле. Проводник пересекает линии магнитного поля и в нем индуктируется напряжение. Величина этого напряжения зависит от силы магнитного поля, скорости движения проводника в этом поле, длины проводника, а так же угла, под которым проводник пересекает линии магнитного поля.

Так как проводник вращаясь постоянно меняет угол под которым он пересекает линии магнитного поля, то ток в нем будет изменяться согласно синусоидальному закону. Это означает, что ток будет менять свое направление и значение. Промежутки времени через которые значения переменного тока повторяются называются периодом Т. Количество периодов за единицу времени называется частотой переменного тока n. По стандарту принята частота переменного тока в сети равна 50 герц. Это означает, что за 1 сек. ток меняет свое значение 50 раз, совершая при этом 50 полных периодов.

Переменный ток постоянно меняет свое значение и в каждый момент времени (мгновение) имеет мгновенное значение. Это значение с течением периода изменяется от минимума к максимальному значению (амплитудному) и обратно. Действия тока не определяют ни амплитудным, ни мгновенным значением. Для оценки действия, производимого переменным током, его сравнивают с действиями теплового эффекта постоянного тока. Для синусоидального переменного тока и напряжения, действующие значения меньше максимальных в раз. Электроизмерительные приборы показывают действующие значения тока или напряжения.

Активное и реактивное сопротивление переменному току. Так же как и постоянному току проводники оказывают переменному току электрическое сопротивление, называемое активным сопротивлением. Для переменного тока так же как и для постоянного справедлив законно Ома.

В цепи может присутствовать емкость и индуктивность, которые оказывают переменному току реактивное сопротивление, а в цепи с постоянным током реактивное сопротивление отсутствует. Следовательно для расчета электрической цепи с переменным током с помощью закона Ома необходимо учитывать как активное, так и реактивное: (емкостное и индуктивное) сопротивление.

Емкостью обладают конденсаторы включенные в цепь, а кроме того сама цепь может обладать собственной емкостью (фарад). Эта емкость оказывает сопротивление току называемое емкостным сопротивлением Х_С. Емкостное сопротивление зависит от величины емкости С, а так же от частоты тока n. Чем больше емкость и частота тока, тем меньше сопротивление.

Индуктивностью обладает любая катушка включенная в цепь, будь то катушка реле или обмотка электродвигателя, оказывает сопротивление электрическому току, но в отличие от емкостного сопротивления при повышении частоты и индуктивности индуктивное сопротивление Х_L увеличивается.

Как было бы логично предположить, для получения общего реактивного сопротивления необходимо сложить индуктивное и емкостное сопротивление, однако индуктивное и емкостное сопротивления оказывают противоположные влияния на ток (напряжения на катушке и на конденсаторе всегда действуют навстречу друг другу). Поэтому формула расчета реактивного сопротивления выглядит так:

Необходимо отметить, что на преодоление активного сопротивления током тратится энергия которая переходит в тепло и теряется безвозвратно, на преодоление же реактивного сопротивления энергия не тратится, а циркулирует переходя из одного вида в другой. На самом деле ток не может течь через конденсатор, поскольку между обкладками есть разрыв. Переменный ток только перезаряжает конденсатор. При заряде конденсатор оказывает сопротивление току, но при разряде он отдает энергию в цепь. Индуктивность оказывает сопротивление нарастающему току поскольку создается магнитное поле препятствующее его прохождению. При падении напряжения индуктивность будет поддерживать ток за счет ЭДС самоиндукции. Другой особенностью цепи переменного тока содержащего емкость и индуктивность является несовпадение фаз напряжения и тока. Ток отстает от напряжения. Это отставание характеризуется коэффициентом смещения фаз φ.

14.Простейший генератор переменного тока. Представляет собой проводник вращающийся в постоянном магнитном поле. Проводник пересекает линии магнитного поля и в нем индуктируется напряжение. Величина этого напряжения зависит от силы магнитного поля, скорости движения проводника в этом поле, длины проводника, а так же угла, под которым проводник пересекает линии магнитного поля.

Так как проводник вращаясь постоянно меняет угол под которым он пересекает линии магнитного поля, то ток в нем будет изменяться согласно синусоидальному закону. Это означает, что ток будет менять свое направление и значение. Промежутки времени через которые значения переменного тока повторяются называются периодом Т. Количество периодов за единицу времени называется частотой переменного тока n. По стандарту принята частота переменного тока в сети равна 50 герц. Это означает, что за 1 сек. ток меняет свое значение 50 раз, совершая при этом 50 полных периодов.

Переменный ток постоянно меняет свое значение и в каждый момент времени (мгновение) имеет мгновенное значение. Это значение с течением периода изменяется от минимума к максимальному значению (амплитудному) и обратно. Действия тока не определяют ни амплитудным, ни мгновенным значением. Для оценки действия, производимого переменным током, его сравнивают с действиями теплового эффекта постоянного тока. Для синусоидального переменного тока и напряжения, действующие значения меньше максимальных в раз. Электроизмерительные приборы показывают действующие значения тока или напряжения.

Активное и реактивное сопротивление переменному току. Так же как и постоянному току проводники оказывают переменному току электрическое сопротивление, называемое активным сопротивлением. Для переменного тока так же как и для постоянного справедлив законно Ома.

В цепи может присутствовать емкость и индуктивность, которые оказывают переменному току реактивное сопротивление, а в цепи с постоянным током реактивное сопротивление отсутствует. Следовательно для расчета электрической цепи с переменным током с помощью закона Ома необходимо учитывать как активное, так и реактивное: (емкостное и индуктивное) сопротивление.

Емкостью обладают конденсаторы включенные в цепь, а кроме того сама цепь может обладать собственной емкостью (фарад). Эта емкость оказывает сопротивление току называемое емкостным сопротивлением Х_С. Емкостное сопротивление зависит от величины емкости С, а так же от частоты тока n. Чем больше емкость и частота тока, тем меньше сопротивление.

Индуктивностью обладает любая катушка включенная в цепь, будь то катушка реле или обмотка электродвигателя, оказывает сопротивление электрическому току, но в отличие от емкостного сопротивления при повышении частоты и индуктивности индуктивное сопротивление Х_L увеличивается.

Как было бы логично предположить, для получения общего реактивного сопротивления необходимо сложить индуктивное и емкостное сопротивление, однако индуктивное и емкостное сопротивления оказывают противоположные влияния на ток (напряжения на катушке и на конденсаторе всегда действуют навстречу друг другу). Поэтому формула расчета реактивного сопротивления выглядит так:

Необходимо отметить, что на преодоление активного сопротивления током тратится энергия которая переходит в тепло и теряется безвозвратно, на преодоление же реактивного сопротивления энергия не тратится, а циркулирует переходя из одного вида в другой. На самом деле ток не может течь через конденсатор, поскольку между обкладками есть разрыв. Переменный ток только перезаряжает конденсатор. При заряде конденсатор оказывает сопротивление току, но при разряде он отдает энергию в цепь. Индуктивность оказывает сопротивление нарастающему току поскольку создается магнитное поле препятствующее его прохождению. При падении напряжения индуктивность будет поддерживать ток за счет ЭДС самоиндукции. Другой особенностью цепи переменного тока содержащего емкость и индуктивность является несовпадение фаз напряжения и тока. Ток отстает от напряжения. Это отставание характеризуется коэффициентом смещения фаз φ.

15. При расчете электрических цепей часто приходится складывать или вычитать величины токов или напряжений, являющиеся синусоидальными функциями времени. Графические построения или тригонометрические преобразования в этом случае могут оказаться слишком громоздкими. Для упрощения расчетов пользуются либо векторным представлением тригонометрических функций, либо комплексным представлением.

Задача упрощается, если представить наши синусоидальные функции в векторной форме. Имеем синусоидальную функцию 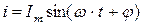. Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону.

Пусть отрезок прямой длиной I_m начинает вращаться вокруг оси " 0 ", ось направлена на нас из толчки “ 0 ”, из положения, когда он образует с горизонтальной осью угол φ, и вращается против часовой стрелки с постоянной угловой скоростью ω. Проекция отрезка на вертикальную ось в начальный момент времени 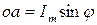. Когда отрезок повернется на угол α ₁, проекция его . Откладывая углы α ₁, α ₂,... на горизонтальной оси, а проекции отрезка прямой - на вертикальной оси, получим ряд точек синусоиды (рис. 3.1).

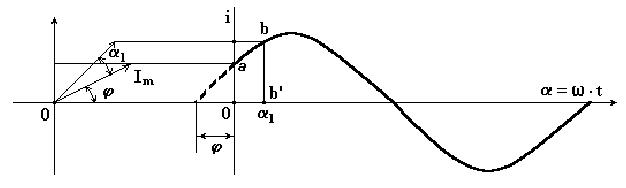
Рисунок 3.1. Вектор на координатной плоскости, соответствующий синусоидальной зависимости тока i с амплитудой I_m от времени t с частотой ω и начальной фазой φ.

Представим синусоидальные токи i₁ и i₂ в виде двух радиус - векторов, длина которых равна в соответствующем масштабе амплитудам соответствующих переменных токов I_1m и I_2m. Эти векторы расположены в начальный момент времени под углами φ ₁ и φ ₂ относительно горизонтальной оси. Сложим геометрически отрезки I_1m и I_2m. Получим отрезок, длина которого равна амплитудному значению результирующего тока I_3m. Отрезок расположен под углом φ ₃ относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными для рассмотрения, данные отрезки образуют векторную диаграмму (рис. 3.2).Векторная диаграмма - это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты.

Рисунок 3.2. Сложение в векторной форме синусоидальных токов с амплитудами I_1m и I_2m и начальными фазами φ ₁ и φ ₂ и результирующий ток I_3m с начальной фазой ψ ₃. Все три тока колеблются с одной и той же частотой ω.

Необходимо отметить, что напряжение, ток и ЭДС - это скалярные, а не векторные величины. Мы представляем их на векторной диаграмме в виде не пространственных, а временных радиус - векторов, вращающихся с одинаковой угловой скоростью, длины этих векторов равны амплитудам соответствующих величин (тока, напряжения, ЭДС). Положительным считается направление вращения векторов против часовой стрелки.

17.

Определите закон Ома для цепи переменного тока, содержащей R, L и С:
Ответ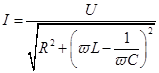
Физическая энциклопедия Т.3, стр. 404 - 405	ОМА ЗАКОН - линейная связь между силой тока I на участке электрич. цепи и приложенным к этому участку напряжением U (интегральная форма О. з.) или между плотностью тока j и напряжённостью электрич. поля в проводнике (дифференц. форма О. з.). О. з. в интегральной форме установлен в 1826 Г. Омом (G. Ohm): U = RI, (1) где R - коэф., зависящий от материала проводника, его геометрии, темп-ры и называемый омическим сопротивлением или просто сопротивлением. Соотношение (1) описывает участок электрич. цепи в отсутствие источников электродвижущей силы. Чтобы в замкнутой системе проводников (электрич. цепи) мог течь стационарный ток, в этой системе должны быть участки, где действуют электрич. поля неэлектростатич. происхождения. Эти участки наз. источниками эдс. Если 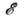- эдс, действующая в неразветвлённой цепи, то вместо (1) имеем где R - полное сопротивление замкнутой цепи, включающее внутр. сопротивление источника эдс. Это соотношение паз. О. з. для замкнутой цепи. Обобщение (2) на случай разветвлённых цепей см. в ст. Кирхгофа правила. О. з. обобщается на случай переменных (меняющихся по гармонич. закону) квазистационарных токов и электрич. цепей, содержащих наряду с омическим (или, как говорят в таких случаях, активным) сопротивлением ещё и электрич. ёмкости С и индуктивности L. В этом случае удобно записывать связи между силой тока I и напряжением U в комплексной форме, понимая под истинными значениями этих величин Re I и Re U соответственно. Введениекомплексного сопротивления, или импеданса, приводит к О. з. для цепи переменного тока: U = ZI [напряжение и ток зависят от времени по закону ехр 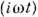]. Мнимая часть в ф-ле (3) наз. реактивным сопротивлением. Правила Кирхгофа остаются в силе и для цепи, включающей наряду с активным (омическим) и реактивные сопротивления; при этом вместо омических сопротивлений участка цепи следует подставить соответствующий импеданс.
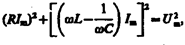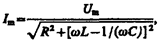Трофимова Т.И. Курс физики, 2001 г., стр. 217	Из прямоугольного треугольника получаем откуда ам­плитуда силы тока имеет значение (149.10) совпадающее с (147.15).
Википедия	Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными: где: U = U 0 ei ω t — напряжение или разность потенциалов, I — сила тока, Z = Re − i δ — комплексное сопротивление (импеданс), R = (Ra 2 + Rr 2)1/2 — полное сопротивление, Rr = ω L − 1/(ω C) — реактивное сопротивление (разность индуктивного и емкостного), Rа — активное (омическое) сопротивление, не зависящее от частоты, δ = − arctg (Rr / Ra) — сдвиг фаз между напряжением и силой тока. При этом переход от комплексных переменных в значениях тока и напряжения к действительным (измеряемым) значениям может быть произведён взятием действительной или мнимой части (но во всех элементах цепи одной и той же!) комплексных значений этих величин. 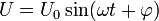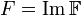Соответственно, обратный переход строится для, к примеру, подбором такой что Тогда все значения токов и напряжений в схеме надо считать как Если ток изменяется во времени, но не является синусоидальным (и даже периодическим), то его можно представить как сумму синусоидальных Фурье-компонент. Для линейных цепей можно считать компоненты фурье-разложения тока действующими независимо. Также необходимо отметить, что закон Ома является лишь простейшим приближением для описания зависимости тока от разности потенциалов и от сопротивления и для некоторых структур справедлив лишь в узком диапазоне значений. Для описания более сложных (нелинейных) систем, когда зависимостью сопротивления от силы тока нельзя пренебречь, принято обсуждатьвольт-амперную характеристику. Отклонения от закона Ома наблюдаются также в случаях, когда скорость изменения электрического поля настолько велика, что нельзя пренебрегать инерционностью носителей заряда.