
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Мощность цепи переменного тока
|
|
Понятие потенциала или разности потенциалов u позволяет определить работу, совершаемую электрическим полем при перемещении элементарного электрического заряда dq, как dA = udq. В то же время, электрический ток равен i = dq / dt. Отсюда dA = ui dt, следовательно, скорость совершения работы, т.е. мощность в данный момент времени или мгновенная мощность равна
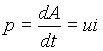 , ,
| (1) |
где u и i - мгновенные значения напряжения и тока.
Величины тока и напряжения, входящие в выражение (1), являются синусоидальными функциями времени, поэтому и мгновенная мощность является переменной величиной и для ее оценки используется понятие средней мощности за период. Ее можно получить, интегрируя за период T работу, совершаемую электрическим полем, а затем соотнося ее с величиной периода, т.е.
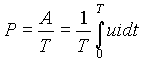 . .
| (2) |
Пусть u = Um sinw t и Im sin(w t -j), тогда средняя мощность будет равна
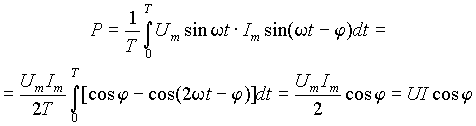
| (3) |
т.к. интеграл второго слагаемого равен нулю. Величина cosj называется коэффициентом мощности.
Из этого выражения следует, что средняя мощность в цепи переменного тока зависит не только от действующих значений тока I и напряжения U, но и от разности фаз j между ними. Максимальная мощность соответствует нулевому сдвигу фаз и равна произведению UI. При сдвиге фаз между током и напряжением в ± 90° средняя мощность равна нулю. Максимальные значения напряжения и тока любой электрической машины определяются ее конструкцией, а максимальная мощность, которую они могут развивать - произведением этих величин. Если электрическая цепь построена нерационально, т.е. сдвиг фаз jимеет значительную величину, то источник электрической энергии и нагрузка не могут работать на полную мощность. Поэтому в любой системе источник-нагрузка существует т.н.
" проблема cosj ", которая заключается в требовании возможного приближения cos j к единице.
Выражение (3) можно представить также с помощью понятий активных составляющих тока I а и напряжения U а в виде
| P = UI cosj = U (I cosj) = UI а = I (U cosj) = IU а. | (4) |
Учитывая, что активные составляющие тока и напряжения можно выразить через резистивную состаляющую комплексного сопротивления цепи как I а= U / R или U а= IR, выражение (4) можно записать также в форме
| P = I 2 R = U 2 /R. | (5) |
Среднюю мощность P называют также активной мощностью и измеряют в ваттах [Вт].
Выделим подинтегральную функцию выражения (3)
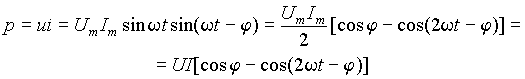
| (6) |
Отсюда следует, что мгновенная мощность изменяется с двойной частотой сети относительно постоянной составляющей UI cosj равной средней или активной мощности.
При cosj = 1 (j = 0), т.е. для цепи, обладающей чисто резистивным сопротивлением
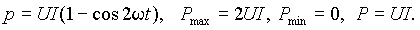
| (7) |
Временные диаграммы, соответствующие этому случаю приведены на рис. 1 а).
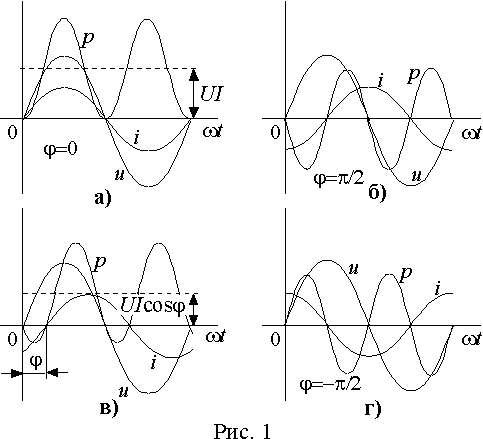
Положительные значения мгновенной мощности соответствуют поступлению энергии от источника в электрическую цепь. Следовательно, при резистивной нагрузке вся энергия поступающая от источника преобразуется в ней в тепло.
При cosj = 0 (j = ± p /2), т.е. для чисто реактивной цепи
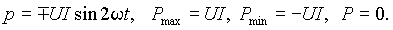
| (8) |
Временные диаграммы, соответствующие чисто индуктивной и чисто емкостной нагрузке приведены на рис. 1 б) и г). Из выражений (8) и временных диаграмм следует, что мощность колеблется относительно оси абсцисс с двойной частотой, изменяя свой знак каждые четверть периода. Это означает, что в течение четверти периода (p > 0) энергия поступает в электрическую цепь от источника и запасается в магнитном или электрическом поле, а в течение следующей четверти (p < 0) она целиком возвращается из цепи в источник. Так как площади, ограниченные участками с положительной мощностью и с отрицательной одинаковы, то средняя мощность отдаваемая источником нагрузке равна нулю и в цепи не происходит преобразования энергии.
В общем случае произвольной нагрузки 1 > cosj > 0 (1< |j | < p /2) и
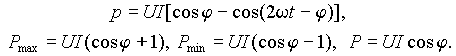
| (8) |
Как следует из временных диаграмм рис. 1 в), большую часть периода мощность потребляется нагрузкой (p > 0), но существуют также интервалы времени, когда энергия запасенная в магнитных и электрических полях нагрузки возвращается в источник. Участки с положительным значением p независимо от характера реактивной составляющей нагрузки всегда больше участков с отрицательным значением, поэтому средняя мощность P положительна. Это означает, что в электрической цепи преобладает процесс преобразования электрической энергии в тепло или механическую работу.
Рассмотрим энергетические процессы в последовательном соединении rLC (рис. 2). Падение напряжения на входе цепи уравновешивается суммой падений напряжения на элементах u = ur + uL + uC. Мгновенная мощность в цепи равна
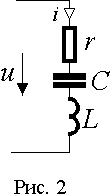 ui = uri + uLi + uCi ui = uri + uLi + uCi
| (9) |
Пусть напряжение и ток на входе равны u = Um sinw t и Im sin(w t -j). Тогда падения напряжения на элементах будут ur = rIm sin(w t -j), uL = w LIm sin(w t -j +p /2) = xLIm sin(w t -j +p /2), uC = Im sin(w t -j -p /2)/(w C) = xCIm sin(w t -j -p /2). Подставляя эти выражения в (9), получим
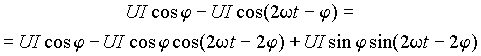
| (10) |
Уравнение (10) в левой и правой частях имеет постоянную и переменную составляющие. Постоянная составляющая представляет собой активную или среднюю мощность. Второе слагаемое в правой части это переменная составляющая активной мощности с амплитудой равной P = UI cosj. Третье слагаемое правой части также является переменной составляющей мгновенной мощности, но эта составляющая находится в квадратуре с переменной составляющей активной мощности и имеет амплитуду Q = UI sinj. Эту величину называют реактивной мощностью. Она равна среднему за четверть периода значению энергии, которой источник обменивается с магнитным и электрическим полями нагрузки. Реактивная мощность не преобразуется в тепло или другие виды энергии, т.к. ее среднее значение за период равно нулю.
Реактивную мощность также можно представить через реактивные составляющие тока или напряжения
| Q = UI sinj = U (I sinj) = UI р = I (U sinj) = IU р. | (11) |
В отличие от всегда положительной активной мощности, реактивная мощность положительна при j > 0 и отрицательна при j < 0.
Из условия равенства переменных составляющих левой и правой частей уравнения (10) можно найти связь между P, Q и S = UI в виде
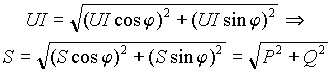
| (12) |
Величина S называется полной или кажущейся мощностью. Из выражения (12) следует, что полную мощность можно представить гипотенузой прямоугольного треугольника с углом j, катетами которого являются активная и реактивная мощности.
Таким образом, полная мощность это максимально возможная активная мощность, т.е. мощность, выделяющаяся в чисто резистивной нагрузке (cosj = 0). Именно эта мощность указывается в паспортных данных электрических машин и аппаратов.
Реактивные составляющие токов и напряжений можно представить через активные и реактивные составляющие комплексного сопротивления, тогда для составляющих мощности
| P = UI а = I 2 R = U а I = U 2/ R = U 2 G; Q = UI р = I 2 X = U р I = U 2/ X = U 2 B; S = UI = I 2 Z = U 2/ Z = U 2 Y. | (13) |
Треугольник мощностей можно описать также с помощью комплексных чисел и изобразить векторами на комплексной плоскости в виде
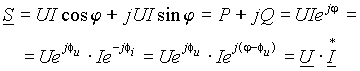 , ,
| (14) |
где S - комплексная полная мощность, 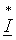 - сопряженный комплексный ток.
- сопряженный комплексный ток.
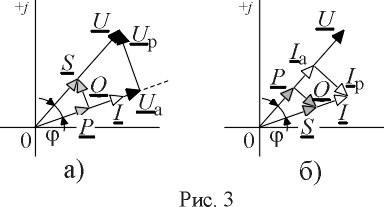 Пользуясь представлением активной и реактивной составляющих мощности через активные и реактивные составляющие токов и напряжений (выражения (4) и (11)), треугольник мощностей можно построить в двух вариантах (рис. 3 а) и б)). В первом случае активная и реактивная составляющие полной мощности выражаются через активную и реактивную составляющие напряжения U и треугольник мощностей получается изменением масштаба треугольника напряжений (рис. 3 а)). Во втором случае (рис. 3 б)), построение выполнено с помощью активной и реактивной составляющих тока I.
Пользуясь представлением активной и реактивной составляющих мощности через активные и реактивные составляющие токов и напряжений (выражения (4) и (11)), треугольник мощностей можно построить в двух вариантах (рис. 3 а) и б)). В первом случае активная и реактивная составляющие полной мощности выражаются через активную и реактивную составляющие напряжения U и треугольник мощностей получается изменением масштаба треугольника напряжений (рис. 3 а)). Во втором случае (рис. 3 б)), построение выполнено с помощью активной и реактивной составляющих тока I.
Очевидно, что все виды мощности имеют одинаковую размерность, поэтому для их отличия от активной мощности, измеряемой в ваттах [Вт], для полной мощности введена единица, называемая вольт-амперы [ВА], а для реактивной мощности - вольт-амперы реактивные [ВАр]
 Выражение для активной мощности P = UI cosj позволяет определить коэффициент мощности с помощью ваттметра, вольтметра и амперметра.
Выражение для активной мощности P = UI cosj позволяет определить коэффициент мощности с помощью ваттметра, вольтметра и амперметра.
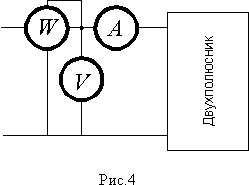
Для этого на вход цепи включают приборы по схеме рис. 4 и по их показаниям определяют коэффициент мощности в виде
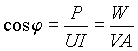 ,
,
где W, V и A - показания соответственно ваттметра, вольтметра и амперметра действующих значений. Из этого выражения можно также определить угол сдвига фаз j между током и напряжением на входе двухполюсника.
29. Две катушки с сопротивлениями R1 и R2, индуктивностями L1 и L 2 и взаимной индуктивностью М соединены последовательно. Возможны два вида их включения: согласное (рис. 4.4а) и встречное (рис. 4.4б).
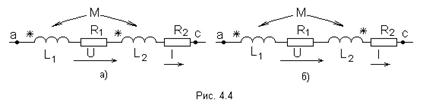
При согласном включении токи в обоих элементах в любой момент времени направлены одинаково относительно одноименных выводов, поэтому магнитные потоки самоиндукции Ф11 (или Ф22 ) и взаимной индукции Ф12 (или Ф21 ), сцепленные с каждым элементом, складываются. При встречном включении токи в обоих элементах цепи в любой момент времени направлены противоположно относительно одноименных выводов, поэтому магнитные потоки самоиндукции и взаимной индукции, сцепленные с каждым элементом, вычитаются.
Индуктивность двух последовательно соединенных индуктивно связанных элементов определяется выражением:
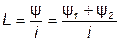 , (4.7)
, (4.7)
где 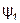 и
и 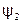 - потокосцепления первого и второго элементов, причем
- потокосцепления первого и второго элементов, причем 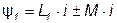 ;
;  .
.
Знак плюс относится к согласному, а знак минус ко встречному включению. Следовательно,
L = L1 + L2 ± 2M.
Полное сопротивление при согласном включении больше, чем при встречном.
Напряжения на элементах имеют по три составляющие:
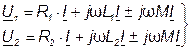 (4.8)
(4.8)
Если индуктивность одного из элементов меньше взаимной индуктивности, то при встречном включении наблюдается своеобразный «емкостный» эффект. Пусть, например, L2 < М, при этом в выражении
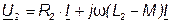
имеем ω (L2-M) < 0, и, следовательно, напряжение 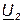 отстает по фазе от тока
отстает по фазе от тока 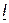 , как в случае емкостного сопротивления. Конечно, реактивное сопротивление всей цепи в целом индуктивное, так как L = L1+ L2 - 2М > 0 и ток
, как в случае емкостного сопротивления. Конечно, реактивное сопротивление всей цепи в целом индуктивное, так как L = L1+ L2 - 2М > 0 и ток 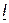 отстает по фазе от напряжения
отстает по фазе от напряжения  .
.
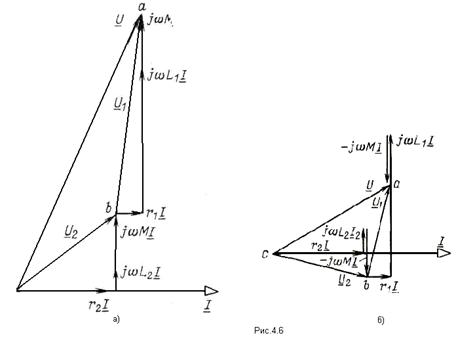
На (рис. 4.5а, б) показаны векторные диаграммы для согласного и встречного включений при одинаковом значении тока в обоих случаях.
Входное комплексное сопротивление цепи получаем, учитывая (4.8)
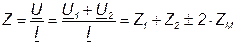 ; (4.9)
; (4.9)
где 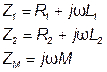 (4.10)
(4.10)
Параллельное соединение индуктивно связанных элементов цепи
Две катушки с сопротивлениями R1 и R2, индуктивностями L1 и L 2 и взаимной индуктивностью М соединены параллельно, причем одноимённые выводы присоединены к одному и тому же узлу (рис. 4.7).

При выбранных положительных направлениях токов и напряжения получаем следующие выражения:
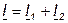 ; (4.11)
; (4.11)
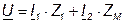 ; (4.12)
; (4.12)
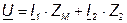 ; (4.13)
; (4.13)
где 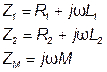 (4.14)
(4.14)
В этих уравнениях комплексные напряжения  и
и 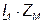 взяты со знаком плюс, так как положительные направления этих напряжений (выбранные сверху вниз) и тех токов, от которых эти напряжения зависят, ориентированы относительно одноименных выводов одинаково. Решив уравнения, получим
взяты со знаком плюс, так как положительные направления этих напряжений (выбранные сверху вниз) и тех токов, от которых эти напряжения зависят, ориентированы относительно одноименных выводов одинаково. Решив уравнения, получим
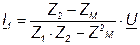 ; (4.15)
; (4.15)
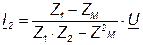 ; (4.16)
; (4.16)
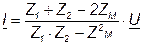 . (4.17)
. (4.17)
Откуда следует, что входное комплексное сопротивление рассматриваемой цепи
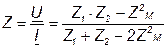 . (4.18)
. (4.18)
Рассмотрим теперь включение, при котором одноименные выводы присоединены к разным узлам, т. е. L1 и L2 присоединены к узлу разноименными выводами. В этом случае положительные направления напряжений взаимной индукции (выбранные сверху вниз) и тех токов, от которых они зависят, ориентированы относительно одноименных выводов неодинаково и комплексные напряжения 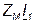 и
и 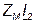 войдут в уравнения (4.12) и (4.13) со знаком минус. Для токов
войдут в уравнения (4.12) и (4.13) со знаком минус. Для токов 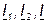 получатся выражения, аналогичные (4.15-4.17), с тем отличием, что ZМ заменяется на - ZМ и входное сопротивление цепи
получатся выражения, аналогичные (4.15-4.17), с тем отличием, что ZМ заменяется на - ZМ и входное сопротивление цепи
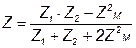 . (4.19)
. (4.19)
30. Параллельное соединение индуктивно связанных элементов цепи
Предположим, что две катушки или два каких-либо элемента цепи с сопротивлениями  и
и 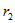 , индуктивностями
, индуктивностями 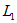 и
и 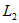 и взаимной индуктивностью М соединены параллельно, причем одноименные выводы присоединены к одному и тому же узлу (рис. 6.9).
и взаимной индуктивностью М соединены параллельно, причем одноименные выводы присоединены к одному и тому же узлу (рис. 6.9).
При выбранных положительных направлениях токов и напряжения

где 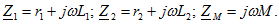
В этих уравнениях комплексные напряжения 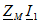 и
и 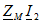 взяты со знаком плюс, так как положительные направления этих напряжений (выбранные сверху вниз) и тех токов, от которых эти напряжения зависят, ориентированы относительно одноименных выводов одинаково.
взяты со знаком плюс, так как положительные направления этих напряжений (выбранные сверху вниз) и тех токов, от которых эти напряжения зависят, ориентированы относительно одноименных выводов одинаково.
Решив уравнения, получим
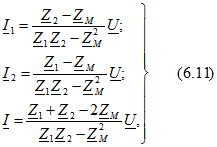
откуда следует, что входное комплексное сопротивление рассматриваемой цепи
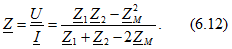
При  , т. е. при отсутствии индуктивной связи между ветвями, это выражение принимает знакомый вид:
, т. е. при отсутствии индуктивной связи между ветвями, это выражение принимает знакомый вид:
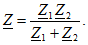
Рассмотрим теперь включение, при котором одноименные выводы присоединены к разным узлам, т. е. 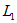 и
и 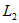 присоединены к узлу разноименными выводами, а не как указано на рис. 6.9. В этом случае положительные направления напряжений взаимной индукции (выбранные сверху вниз) и тех токов, от которых они зависят, ориентированы относительно одноименных выводов неодинаково и комплексные напряжения
присоединены к узлу разноименными выводами, а не как указано на рис. 6.9. В этом случае положительные направления напряжений взаимной индукции (выбранные сверху вниз) и тех токов, от которых они зависят, ориентированы относительно одноименных выводов неодинаково и комплексные напряжения 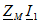 и
и 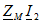 войдут в уравнения (6.9) и (6.10) со знаком минус. Для токов
войдут в уравнения (6.9) и (6.10) со знаком минус. Для токов 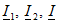 получатся выражения, аналогичные (6.11), с тем отличием, что
получатся выражения, аналогичные (6.11), с тем отличием, что 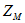 заменяется на
заменяется на 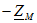 и входное сопротивление цепи
и входное сопротивление цепи
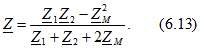
27.
Если изменение тока в одном из элементов электрической цепи приводит к возникновению Э.Д.С. в другом элементе цепи, то говорят, что эти элементы индуктивно связаны друг с другом. Возникающая при этом Э.Д.С. называется Э.Д.С. взаимной индукции.
На (рис. 4.1) показаны две катушки с числом витков и магнитный поток первой катушки пропорционален протекающему по ней току. Часть этого потока пронизывает витки второй катушки и оказывает влияние на ток.
Аналогично магнитный поток второй катушки пронизывает витки первой.
Такие катушки называются индуктивно – связанными (или магнитно-связанными).
Степень индуктивной связи двух элементов цепи характеризуется коэффициентом связи k, который определяется отношением:
, (4.1)
где М - взаимная индуктивность элементов цепи, Гн.
- индуктивности элементов, Гн.
Необходимо запомнить, что коэффициент связи не может быть больше единицы!
Вообще, взаимной индуктивностью первой и второй катушек называется отношение добавочного потокосцепления второй катушки к току первой катушки:
; (4.2)
; (4.3)
. (4.4)
Индекс 12 показывает, что взаимная индуктивность наводится в первой катушке от действия магнитного потока второй катушки.
Опыт показывает, что:
Справедливо соотношение:
. (4.5)
Взаимная индуктивность в линейных электрических цепях не зависит от направлений и значений токов, и определяется только конструкцией катушек их взаимным расположением. Об этом также свидетельствует выражение (4.5).
Индуктивность катушки определяется по формуле:
, (4.6)
где - относительная магнитная проницаемость среды (для воздуха);
- абсолютная магнитная проницаемость среды;
S – площадь поперечного сечения катушки, мм2;
L - длина катушки, м.
При составлении уравнений для магнитно-связанных цепей необходимо знать, согласно или встречно направлены потоки самоиндукции и взаимоиндукции. Правильное заключение об этом можно сделать, если известно направление намотки катушек на сердечнике и выбрано положительное направление токов в них.
На (рис. 4.2а) катушки включены согласно, а на (рис. 4.2б) – встречно.
На рис. 4.2 одноимённые зажимы (например, начала катушки) – помечают одинаковыми значками, например точками.
Если на электрической схеме токи двух магнитно-связанных катушек направлены одинаково относительно одноимённых обозначенных зажимов, например оба тока направлены к точкам как на (рис. 4.2а), то катушки соединены согласно, в противном случае встречно.
На практике часто возникает трудность в определении одинаковых выводов катушек. Для этой цели используют простой опыт, для которого требуется гальванический элемент (или аккумулятор) и гальванометр (или вольтметр).
Одна из катушек соединяется с вольтметром, другая подключается к гальваническому элементу (рис. 4.3). При замыкании ключа К во второй катушке кратковременно возникает ток, ослабляющий магнитное поле, созданное током. Направление тока определяется полярностью источника питания. О направлении тока судят по кратковременному отклонению стрелки вольтметра. Если стрелка отклоняется в сторону шкалы (то есть не зашкаливает), то ток направлен к положительному выводу вольтметра, при этом выводы катушек, присоединённых к положительным выводам вольтметра и источника питания, одноимённы.
На (рис. 4.3) при указанных направлениях токов и полярности вольтметра, соединение катушек – встречное.
49. Под активной мощностью P понимают количество энергии, потребляемое (генерируемое) объектом за единицу времени. Математически активную мощность определяют как среднее значение мгновенной мощности за полный период.
Пусть некоторый элемент цепи потребляет ток i(t) при несинусоидальном напряжении u(t):

Мгновенная мощность p(t)=u(t)*i(t), тогда активная мощность будет равна:

Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник:
P=P0+P1+P2+P3...
Реактивная мощность Q несинусоидального тока определяется по аналогии с активной мощностью P как алгебраическая сумма реактивных мощностей отдельных гармоник:
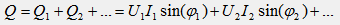
Как известно, реактивная мощность Q синусоидального тока характеризует интенсивность колебаний энергии (Q=ω Wmax) с частотой ω между элекромагнитным полем элемента и остальной цепью. В цепи несинусоидального тока колебания энергии происходят на разных частотах. Сложение реактивных мощностей отдельных гармоник, характеризующих колебания энергии на разных частотах, лишено физического смысла. Математически может получиться, что реактивные мощности отдельных гармоник имеют разные знаки и в сумме дают нуль, хотя колебания энергии при этом имеют место. Таким образом, для цепи несинусоидального тока понятие реактивной мощности лишено физического смысла.
Для цепи несинусоидального тока применяется также и понятие полной мощности, которая определяется как произведение действующих значений напряжения и тока:
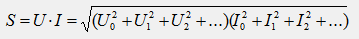
Как известно, для цепи синусоидального тока мощности P, Q, S образуют прямоугольный треугольник, из которого следует соотношение: S2=P2+Q2. Для цепей несинусоидального тока это соотношение между мощностями выполняется только для резистивных элементов, в которых в соответствии с законом Ома (u=iR) формы кривых функций u(t) и i(t) идентичны. Если в цепи содержатся реактивные элементы L и С, то это соотношение не выполняется: S2≥ P2+Q2. Для баланса этого уравнения в его правую часть вносят добавление: S2≥ P2+Q2+T2, откуда
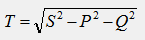
где Т - мощность искажения – понятие математическое, характеризует степень различия в формах кривых напряжение u(t) и тока i(t).
20.
Вектор синусоидально изменяющейся величины может быть представлен и на комплексной плоскости. Комплексные представления позволяют совместить простоту и наглядность векторных диаграмм, имеющим недостаток – ограниченную точность, с возможностью проведения точных аналитических расчетов. При оперировании с векторами можно воспользоваться теорией, разработанной для комплексных чисел. Вектору, расположенному на комплексной плоскости, однозначно соответствует комплексное число. В соответствии с формулой Эйлера для комплексного числа равнозначны алгебраическая, тригонометрическая и показательная формы записи. При суммировании комплексных чисел удобна алгебраическая форма, при умножении и делении – показательная.
Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока.
Следует обратить внимание на то, что комплексные изображения, как и векторные диаграммы, несут информацию только о двух параметрах синусоиды – амплитуде и начальной фазе, не отражая ее третьего параметра – угловую частоту ω. Векторы на комплексной плоскости и соответствующие им комплексные числа принято изображать той же буквой, что и амплитуду изображаемой синусоиды с точкой наверху.
Мнимая единица в электротехнике обозначается символом j, поскольку символ i используется для обозначения мгновенного тока.
Ток i(t) = Im sin(ω t + φ о) можно представить комплексным числом Í m на комплексной плоскости
где амплитуда тока Im – модуль, а угол φ о, являющийся начальной фазой, – аргумент комплексного тока.
Все параметры цепи представляются в комплексной форме.
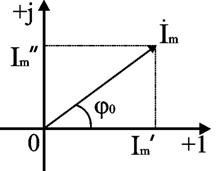
Алгебраическая форма записи комплексного числа: İ m = Im’ + j Im’’, при записи в тригонометрической форме проекции вектора выражают через его длину Im и угол φ о: İ m = Imcosφ о + j Imsinφ о = Im(cosφ о + j sinφ о). Показательная форма записи имеет вид İ m = Ime jφ о .
В этих выражениях Im = √ (Im’ 2+ Im’’2 ) – модуль комплексного числа, φ о = arctg(Im’’/ Im’) - его аргумент, Im’= Imcos φ о, Im’’= Imsin φ о.
 – комплексное действующее значение силы тока (без индекса m); здесь I = Im /√ 2;
– комплексное действующее значение силы тока (без индекса m); здесь I = Im /√ 2;
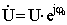 – комплексное действующее значение напряжения (без индекса m); U =Um /√ 2.
– комплексное действующее значение напряжения (без индекса m); U =Um /√ 2.
Пример, представить комплексное действующее значение тока 
в показательной форме. Ответ:
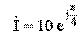 .
.