
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Выберем направления токов , и обхода в контуре, составим уравнения по законам Кирхгофа
|
|
Выберем направления токов 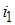 ,
, 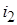 и обхода в контуре, составим уравнения по законам Кирхгофа. Число уравнений, составляемых по первому закону Кирхгофа:
и обхода в контуре, составим уравнения по законам Кирхгофа. Число уравнений, составляемых по первому закону Кирхгофа:
 .
.
Число уравнений по второму закону Кирхгофа:
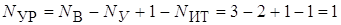 .
.
Уравнение токов для узла 1:
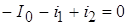 . (a)
. (a)
Уравнение по второму закону Кирхгофа:
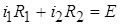 . (б)
. (б)
Подставим в уравнения (а) и (б) числовые значения получим:
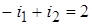 ,
,
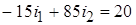 .
.
Решив эту систему, определим токи 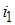 и
и 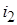 :
:
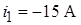 ;
; 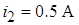 .
.
7. Расчет сложных электрических цепей давно перестал составлять трудности не только для специалистов, но и для большинства более успевающих студентов электротехнических ВУЗов и техникумов.
В настоящее время разработаны программы с графическим интерфейсом, позволяющие буквально за несколько минут рассчитать самую сложную цепь и определить все ее параметры.
Однако, в основе программных и " ручных" расчетов лежат методы, разработанные достаточно давно. Эти методы основаны на основных законах электротехники: прежде всего, на законах Ома и Кирхгофа. Одним из наиболее популярных методов расчета сложной цепи является метод контурных токов (далее - КТ). Поговорим о нем подробнее.
Основу метода КТ составляет предположение о том, что по каждому замкнутому контуру сложной цепи протекает некий свой КТ. Этот ток, хотя его и можно объявить воображаемым, все же подчиняется известным нам законам: имеет постоянную величину на протяжении всего контура, создает падение напряжения на каждом элементе.
Яндекс.Директ
 Размещаем объявления о вакансиях! Подай бесплатное объявление о вакансии в газету «Только вакансии и резюме»! v-i-r.com.ua Размещаем объявления о вакансиях! Подай бесплатное объявление о вакансии в газету «Только вакансии и резюме»! v-i-r.com.ua
|
Естественно, в некоторых ветвях цепи будут пересекаться два разных КТ. В таком случае, ток этой ветви будет найден как алгебраическая сумма этих КТ. Ну а в тех ветвях, где протекает всего один КТ, он и будет определять величину тока.
Таким образом, для решения задачи методом КТ нам необходимо задаться в каждом контуре своим КТ с произвольным направлением, чаще всего, совпадающим с направлением хода часовой стрелки.
Обычно, контуры нумеруются цифрами в порядке от единицы и далее. КТ обозначаются индексом с двойным указанием номера контура, например, I11, I22 и так далее. Это делается для того, чтобы впоследствии не перепутать их с токами в ветвях, которые обозначаются одиночным индексом с номером ветви: I1, I2.
После обозначения КТ и присвоения им направления в действие вступает второй закон Кирхгофа. Сумма падений напряжения в каждом контуре равна сумме ЭДС. А падения напряжения находятся как произведение КТ на сопротивление элемента цепи.
Причем, если направление КТ совпадает с направлением обхода контура, то значение падения напряжения, вызванного этим током, принимается положительным, а если не совпадает – отрицательным.
Та же ситуация и со знаком при ЭДС, имеющихся в контуре и располагающихся в правой части равенства по закону Кирхгофа: если направление ЭДС совпадает с направлением обхода контура, то она положительная, а если не совпадает – отрицательная.
Итак, мы получаем уравнения для каждого контура. Число этих уравнений равно числу КТ, то есть числу неизвестных. А это значит, что мы получаем систему уравнений, решить которую можно любым известным способом: методом подстановки, либо методом Гаусса.
Главное, что в итоге мы получим значения КТ. Причем, если какие-то из этих значений окажутся отрицательными, то это просто значит, что изначально мы задались неверным направлением для этого КТ.
Токи в ветвях найдутся уже именно как суммы КТ, протекающих в этих самых ветвях. Проверку можно выполнить по первому закону Кирхгофа: сумма токов в каждом узле цепи должна быть равна нулю.
Пример решения. Ниже приведем элементарный пример решения сложной цепи по методу КТ.
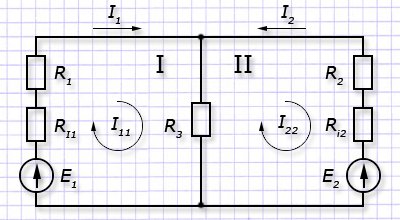
Видно, что в примере есть два контура: 1 и 2. И есть два КТ I11 и I22. Составляем систему уравнений для первого и второго контуров соответственно:
I11(R1+Ri1+R3)–I22R3=E1;
– I11R3+I22(R2+Ri2+R3)=–E2
Решаем эту систему, скажем, методом подстановки:
Из первого уравнения: I11=(I22R3+E1)/(R1+Ri1+R3);
Из второго уравнения: – ((I22R3+E1)/(R1+Ri1+R3))R3+I22(R2+Ri2+R3)=–E2;
Или: I22(R2+Ri2+R3)–(I22R32)/(R1+Ri1+R3)–(E1R3)/(R1+Ri1+R3)=–E2.
После расчетов получаем выражение:
I22(R2+Ri2+R3–(R32)/(R1+Ri1+R3))=(E1R3)/(R1+Ri1+R3)–E2.
Находим I22:
I22=((E1R3)/(R1+Ri1+R3)–E2)/(R2+Ri2+R3–(R32)/(R1+Ri1+R3)).
Полученное значение подставляем в выражение I11=(I22R3+E1)/(R1+Ri1+R3) и находим I11. Далее находим значения токов в ветвях:
I1=I11;
I2=I22;
I3=I11+I22.