
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
реугольники напряжений, токов, сопротивлений и проводимостей
|
|
Как известно, любая электрическая цепь состоит или может быть представлена в виде двухполюсников. Пассивный двухполюсник однозначно определяется значениями тока и напряжения на входе или их отношением.
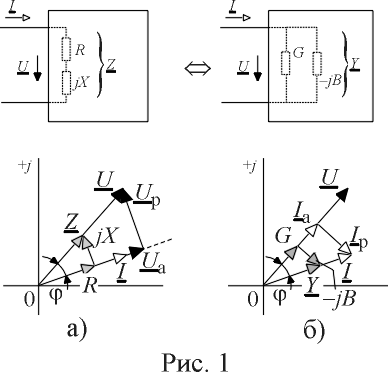 Пусть через некоторый двухполюсник протекает переменный ток и существует падение напряжения. Изобразим ток и напряжение на входе двухполюсника векторами на комплексной плоскости I и U (рис. 1).
Пусть через некоторый двухполюсник протекает переменный ток и существует падение напряжения. Изобразим ток и напряжение на входе двухполюсника векторами на комплексной плоскости I и U (рис. 1).
Проектируя вектор U на направление вектора I (рис. 1 а)), получим вектор, модуль которого равен U а= U cosj, где j - разность начальных фаз напряжения и тока на входе двухполюсника, причем, направление вектора U а совпадает с направлением вектора тока, поэтому его запись в показательной форме будет иметь вид
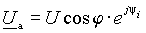 , ,
| (1) |
где y i - начальная фаза тока на входе двухполюсника.
Перпендикуляр, опущенный из конца вектора U на направление вектора тока, имеет длину U sinj и может рассматриваться как некоторый вектор U р, сумма которого с вектором U а равна U (рис. 1 а)). Его также можно записать в показательной форме в виде
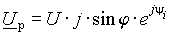 . .
| (2) |
Оператор поворота j в выражении (2) учитывает перпендикулярное положение вектора U р по отношению к I и условие U а + U р = U.
Так как по построению векторы U а и U р в сумме равны U, то из выражений (1) и (2) вектор напряжения на входе двухполюсника можно представить как
 . .
| (3) |
Разделим выражение (3) на модуль вектора тока
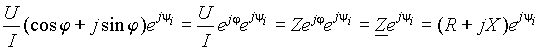 . .
| (4) |
Выражение (4) соответствует представлению на комплексной плоскости вектора Z, равного комплексному сопротивлению двухполюсника и развернутого относительно вещественной оси на угол y i. При этом вектор Z e jj e jy i = Z e j (y u- y i +y i)= Z e jy u образует с вещественной осью комплексной плоскости угол y u, т.е. оказывается совпадающим по направлению с вектором U.
Сравнивая вещественные и мнимые части выражений (3) и (4), можно представить модули составляющих вектора U в виде
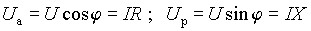 , ,
| (5) |
т.е. модуль составляющей U а, называемой активной или резистивной составляющей напряжения на входе двухполюсника, представляет собой падение напряжения на резистивной составляющей его комплексного сопротивления при токе I. Аналогично, модуль вектора U р, называемого реактивной составляющей входного напряжения, является падением напряжения на реактивной составляющей комплексного сопротивления.
Рассмотренным соотношениям величин соответствует представление двухполюсника последовательным соединением резистора R и реактивного сопротивления X, представленным на рис. 1 а).
Таким образом, вектор падения напряжения на входе двухполюсника может быть представлен двумя составляющими, одна из которых является его проекцией на направление вектора входного тока и называется активной (резистивной) составляющей или активным падением напряжения. Активная составляющая соответствует падению напряжения на резистивном сопротивлении последовательной эквивалентной схемы двухполюсника. Вторая составляющая перпендикулярна вектору тока и соответствует падению напряжения на реактивном сопротивлении последовательной эквивалентной схемы.
Прямоугольные треугольники UU а U р и ZRX (рис. 1 а)) подобны и называются соответственно треугольниками напряжений и сопротивлений.
ЗАДАЧА 1
Спроектируем теперь вектор тока I на направление вектора падения напряжения U (рис. 1 б)). Длина проекции будет равна I а= I cosj, а длина проектирующего перпендикуляра - I р= I sinj. Представим эти отрезки векторами с учетом того, что I а совпадает с направлением вектора падения напряжения на входе двухполюсника, а в сумме эти два вектора должны быть равны I. Тогда в показательной форме -

| (6) |

| (7) |
Множитель - j является оператором поворота отрезка I р на 90° в направлении отставания, чтобы обеспечивалось условие I а + I р = I.
Представим теперь вектор тока через полученные составляющие
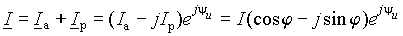 . .
| (8) |
Разделим выражение (8) на модуль вектора U -
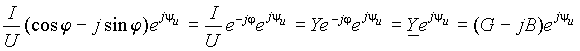 . .
| (9) |
Таким образом, из прямоугольного треугольника, составленного из векторов I а, I р и I и описанного выражением (8), делением на постоянную величину U всех его сторон мы получили подобный треугольник, описываемый выражением (9). Стороны нового треугольника имеют размерность проводимости и связаны с составляющими вектора тока законом Ома
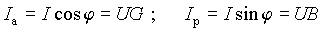 . .
| (10) |
Следовательно, активную и реактивную составляющую вектора тока можно представить, в виде токов, протекающих через активную (резистивную) проводимость G и реактивную проводимость B эквивалентной параллельной схемы двухполюсника (рис. 1 б)).
Прямоугольные треугольники II а I р и YGB (рис. 1 б)) подобны и называются соответственно треугольниками токов и проводимостей. Очевидно, что треугольники токов и проводимостей подобны треугольникам напряжений и сопротивлений, т.к. имеют одинаковые углы.
Обобщая понятия составляющих векторов тока и напряжения на входе двухполюсника, можно сделать следующие выводы:
- активная (резистивная) и реактивная составляющие вектора напряжения на входе двухполюсника соответствуют падениям напряжения на резистивном и реактивном сопротивлениях последовательной эквивалентной схемы (схемы R-X);
- активная (резистивная) и реактивная составляющие вектора тока на входе двухполюсника соответствуют токам, протекающим через резистивную и реактивную проводимости параллельной эквивалентной схемы (схемы G-B);
- понятиями активной и реактивной составляющих тока и напряжения можно пользоваться, не связывая их с какой-либо эквивалентной схемой двухполюсника, т.к. из подобия треугольников напряжений, токов, сопротивлений и проводимостей следует взаимно однозначная связь этих величин.
44. Ниже рассмотрены практические схемы включения ваттметров для измерения мощности в трехфазных цепях.
1. Четырехпроводная система, несимметричный режим.
Представленная на рис. 8 схема называется схемой трех ваттметров.
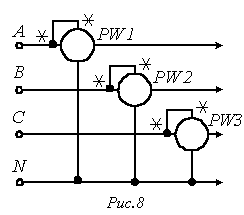 Суммарная активная мощность цепи определяется как сумма показаний трех ваттметров
Суммарная активная мощность цепи определяется как сумма показаний трех ваттметров
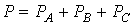 .
.
2. Четырехпроводная система, симметричный режим.
Если режим работы цепи симметричный, то для определения суммарной активной мощности достаточно ограничиться одним ваттметром (любым), включаемым по схеме на рис. 8. Тогда, например, при включении прибора в фазу А,
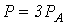 . .
| (4) |
3. Трехпроводная система, симметричный режим.
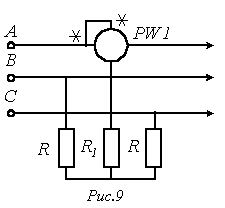 При отсутствии доступа к нейтральной точке последняя создается искусственно с помощью включения трех дополнительных резисторов по схеме «звезда», как показано на рис. 9 – схема ваттметра с искусственной нейтральной точкой. При этом необходимо выполнение условия
При отсутствии доступа к нейтральной точке последняя создается искусственно с помощью включения трех дополнительных резисторов по схеме «звезда», как показано на рис. 9 – схема ваттметра с искусственной нейтральной точкой. При этом необходимо выполнение условия 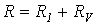 , где
, где 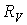 - собственное сопротивление обмотки ваттметра. Тогда суммарная активная мощность трехфазной системы определяется согласно (4).
- собственное сопротивление обмотки ваттметра. Тогда суммарная активная мощность трехфазной системы определяется согласно (4).
4. Трехпроводная система, симметричный режим; измерение реактивной мощности.
С помощью одного ваттметра при симметричном режиме работы цепи можно измерить ее реактивную мощность. В этом случае схема включения ваттметра будет иметь вид по рис. 10, а. Согласно векторной диаграмме на рис. 10, б измеряемая прибором мощность
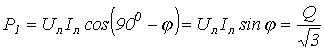 .
.
Таким образом, суммарная реактивная мощность
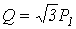 .
.
5. Трехпроводная система, несимметричный режим.
Представленная на рис. 11 схема называется схемой двух ваттметров. В ней сумма показаний приборов равна суммарной активной мощности цепи.
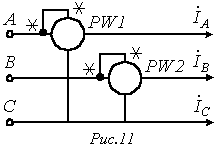
Действительно, показания приборов в данной схеме:
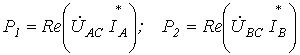 .
.
Тогда
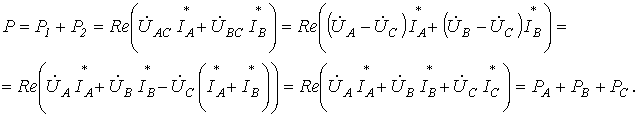
В заключение отметим, что если в схеме на рис. 11 имеет место симметричный режим работы, то на основании показаний приборов можно определить суммарную реактивную мощность цепи
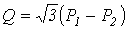 . .
| (5) |
40. Исследование трёхфазных цепей при соединении сопротивлений нагрузки в звезду
Цель работы: экспериментальная проверка соотношений между линейными и фазными величинами и уяснение назначения нулевого провода.
Пояснения к работе
 В зависимости от номинального напряжения приёмника и от параметров сети в трёхфазных системах сопротивления нагрузки могут включаться либо в «звезду», либо в «треугольник». Это две основные схемы включения элементов в 3х- фазных системах. Если комплексы сопротивлений фаз одинаковы: Zа= Zв =Zс=Zф,, то нагрузка называется симметричной, в противном случае – несимметричной. Для величин на зажимах генератора удобно употреблять в качестве индексов большие буквы А, В, С. Для величин на зажимах нагрузки – малые буквы: ax, ву, cz или а, в, с.
В зависимости от номинального напряжения приёмника и от параметров сети в трёхфазных системах сопротивления нагрузки могут включаться либо в «звезду», либо в «треугольник». Это две основные схемы включения элементов в 3х- фазных системах. Если комплексы сопротивлений фаз одинаковы: Zа= Zв =Zс=Zф,, то нагрузка называется симметричной, в противном случае – несимметричной. Для величин на зажимах генератора удобно употреблять в качестве индексов большие буквы А, В, С. Для величин на зажимах нагрузки – малые буквы: ax, ву, cz или а, в, с.
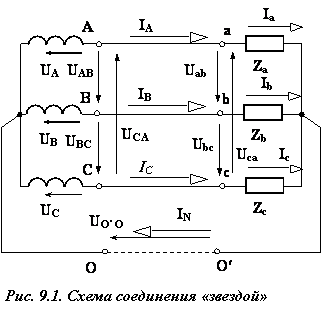
При соединении нагрузки в звезду и симметричном режиме работы цепи (рис. 9.1) линейные и фазные величины связаны между собой соотношениями:
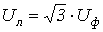 ,
, 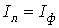 , или в комплексной форме:
, или в комплексной форме:
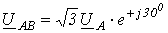 ;
; 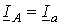 .
.
При несимметричной нагрузке линейные напряжения определяются через фазные по II закону Кирхгофа:
U ab = U a – U b; U bc = U b – U c; U ca = U c – U a.
Линейные и фазные токи при соединении «звезда» это одни и те же токи, только на разных участках своей фазы, т.е.:
I a = I a, I B = I b, I C = I c.
Если нагрузка несимметрична, то между нейтральными точками нагрузки 0¢ и источника 0 возникает узловое напряжение UO¢ O, которое называют напряжением смещения нейтрали. В этом случае:
UO¢ O = 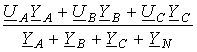 ;
;
Ua = UA – UO¢ O, Ub = UB – UO¢ O, Uc=UC – UO¢ O.
Здесь YA, YB, YC, YN – проводимости фаз нагрузки и нулевого провода;
 UA, B, C – фазные напряжения генератора, Ua, b, c – фазные напряжения нагрузки.
UA, B, C – фазные напряжения генератора, Ua, b, c – фазные напряжения нагрузки.
При несимметричной нагрузке для выравнивания фазных напряжений приёмника применяется нулевой провод (НП). При симметричной нагрузке ток в нулевом проводе равен нулю, и провод, собственно, не нужен. При несимметричной нагрузке ток в нулевом проводе определяется по I закону Кирхгофа:
IN = IA + IB + IC.
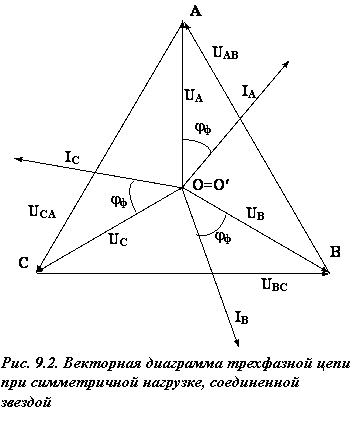
Типовая векторная диаграмма для цепи при симметричной R, L-нагрузке, соединённой в звезду, представлена на рис. 9.2.
Домашняя подготовка к работе
1. Изучить тему «Трёхфазные цепи синусоидального тока», познакомиться с целью и пояснениями к данной лабораторной работе. Подготовить схему и таблицы, необходимые для проведения экспериментов.
2. Для Вашего варианта схемы трёхфазной цепи (см. табл. 8.1) рассчитать токи и напряжения нагрузки и построить векторные диаграммы для трёх случаев: нагрузка симметричная; обрыв сопротивления нагрузки по любой одной из фаз при отсутствии нулевого провода; короткое замыкание по любой другой фазе нагрузки при отсутствии нулевого провода.
Результаты расчётов внести в табл. 2 для сравнения с результатами измерений.
Порядок выполнения работы
1. Используя набор съёмных элементов и элементов на стенде, собрать схему Вашего варианта. Пояснения к формированию сопротивлений нагрузки приведены в примечаниях к таблице вариантов. Нанести общепринятые обозначения сопротивлений и напряжений. В качестве трёхфазного источника использовать источник синусоидального напряжения частотой 50 Гц, имеющийся на стенде.
2. Симметричный режим. Измерить токи Iф, IN, линейные Uab, Ubc, Uca и фазные Ua, Ub, Uc напряжения на нагрузке при включенном и при отключенном нулевом проводе. Результаты измерений внести в табл. 2. Убедиться, что отношение Uл.ср к Uф.ср действительно равно 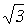 .
.
3. Режим обрыва фазы. Повторить измерения токов и напряжений при обрыве сопротивления нагрузки для случаев включенного и отключенного нулевого провода.
4. Режим короткого замыкания. При выполнении этого эксперимента необходимо пригласить преподавателя. Измерения выполнить только при отключенном нулевом проводе.
5. Сравнить измеренные и расчётные значения токов и напряжений по каждому из пунктов исследования. На векторные диаграммы, построенные при подготовке к работе, другим цветом нанести векторы, соответствующие экспериментальным данным.
46. Метод симметричных составляющих применяется для расчета трехфазных цепей в несимметричных режимах. Несимметричные режимы в энергосистеме возникают при различных видах коротких замыканий. Расчет токов коротких замыканий – важная инженерная задача в электроэнергетике, которая решается методом симметричных составляющих.
Математически любая несимметричная трехфазная система векторных величин (напряжений, токов и др.) может быть представлена в виде суммы (заменена суммой) из трех симметричных трехфазных систем, а именно: а) системы прямой последовательности с прямым порядком следования фаз A→ B→ C→ A; б) системы обратной последовательности с обратным порядком следования фаз A→ C→ B→ A; в) системы нулевой последовательности, которая состоит из трех равных векторов, совпадающих по фазе. Отдельные симмет-ричные системы векторов, на которые раскладывается несимметричная сис-тема, называются симметричными составляющими. Вектора симметричных составляющих индексируются цифрами: 1 - для прямой последовательности, 2 - для обратной последовательности и 0 – для нулевой последовательности.
На рис. 42.1 представлены симметричные составляющие некоторой несимметричной трехфазной системы напряжений UA, UB, UC.
В методе симметричных составляющих для упрощения формы записи уравнений пользуются коэффициентом a=ej120° (поворотный множитель), умножением на который поворачивают вектор на угол в 120° без изменения его модуля. Свойства поворотного множителя: a2=ej240°=e-j120°, a3=1, a4=a, 1+a+a2=0.
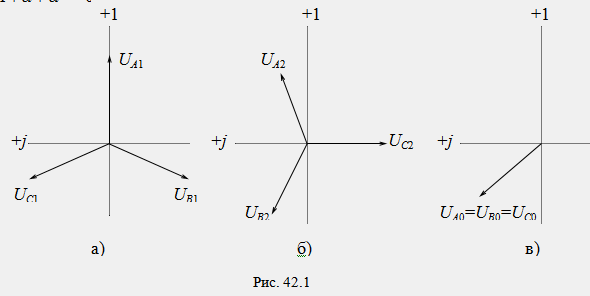
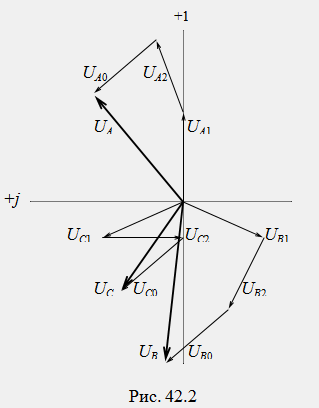
Вектора исходной несимметричной системы определяются по принципу наложения как геометрические суммы соответствующих векторов симметричных составляющих:
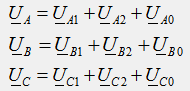
Геометрическое сложение векторов симметричных составляющих согласно этим уравнениям показано на рис. 42.2.
Используя поворотный множитель “a” и “a2”, выразим все слагаемые правой части уравнений через симметричные составляющие фазы А:
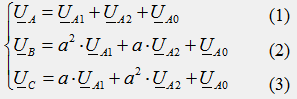
Умножим все члены уравнения (2) на “a”, а все члены уравнения (3) на “a2”, сложим все три уравнения почленно и получим:
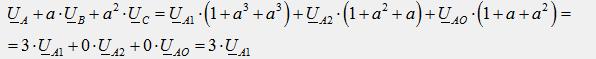
Из полученного уравнения следует формула для выделения симметричной составляющей прямой последовательности из несимметричной системы векторов:
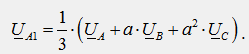
Умножим все члены уравнения (2) на “a2”, а все члены уравнения (3) на “a”, сложим все три уравнения почленно и получим:
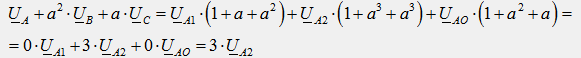
Из полученного уравнения следует формула для выделения симметричной составляющей обратной последовательности из несимметричной системы векторов:
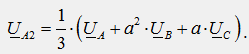
Сложим все три уравнения (1), (2) и (3) почленно и получим:
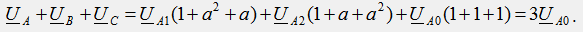
Из полученного уравнения следует формула для выделения симметричной составляющей нулевой последовательности из несимметричной системы вектор:

Полученные формулы применяются на практике для разложения несимметричных трехфазных систем векторов на симметричные составляющие.