
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Момент сили відносно точки та осі. Пара сил
|
|
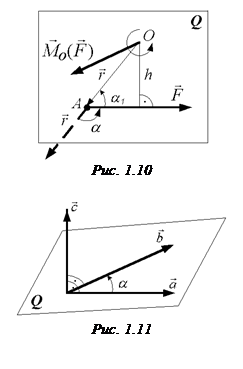
Моментом сили відносно точки 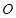 називають векторний добуток
називають векторний добуток
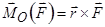 , (1.3)
, (1.3)
де 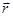 – радіус-вектор, проведений з точки
– радіус-вектор, проведений з точки 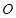 в точку А прикладання сили (рис. 1.10).
в точку А прикладання сили (рис. 1.10).
 Нагадаємо, що векторний добуток
Нагадаємо, що векторний добуток  векторів
векторів  та
та  (рис. 1.11) є вектор, напрямлений перпендикулярно до площини, у якій знаходяться вектори
(рис. 1.11) є вектор, напрямлений перпендикулярно до площини, у якій знаходяться вектори 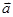 та
та 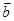 , у той бік, звідки найкоротший поворот від вектора
, у той бік, звідки найкоротший поворот від вектора 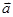 до вектора
до вектора 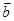 (від першого
(від першого 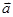 до другого
до другого 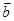 ) видно проти ходу годинникової стрілки (вектори
) видно проти ходу годинникової стрілки (вектори 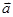 та
та 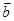 повинні бути
повинні бути  зведеними в одну точку). Можна також зазначити, що момент сили відносно точки напрямлений у той бік, звідки обертання тіла, яке намагається здійснити сила відносно нерухомої точки О, видно проти ходу годинникової стрілки (рис. 1.10). Простіше це можна сформулювати як “правило гвинта”: момент напрямлений у той бік, у який спрямоване зміщення гвинта при його обертанні в напрямі обертання тіла, яке намагається здійснити сила
зведеними в одну точку). Можна також зазначити, що момент сили відносно точки напрямлений у той бік, звідки обертання тіла, яке намагається здійснити сила відносно нерухомої точки О, видно проти ходу годинникової стрілки (рис. 1.10). Простіше це можна сформулювати як “правило гвинта”: момент напрямлений у той бік, у який спрямоване зміщення гвинта при його обертанні в напрямі обертання тіла, яке намагається здійснити сила  . Аналогічно, з використанням “правила гвинта”, можна визначити і напрям вектора
. Аналогічно, з використанням “правила гвинта”, можна визначити і напрям вектора 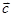 (рис. 1.11).
(рис. 1.11).
Зображаємо вектор  прикладеним в точці О
прикладеним в точці О
(рис. 1.10). Модуль вектора 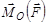 визначається за формулою
визначається за формулою
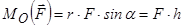 , (1.4)
, (1.4)
де 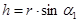 – плече сили
– плече сили  , тобто довжина перпендикуляра, проведеного з точки
, тобто довжина перпендикуляра, проведеного з точки  до лінії дії сили
до лінії дії сили  (рис. 1.10), або плече сили –це найкоротша відстань від точки
(рис. 1.10), або плече сили –це найкоротша відстань від точки  до лінії дії сили
до лінії дії сили  .
.
Момент сили відносно точки можна також визначити, розглядаючи силу у вигляді складових 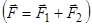 , причому
, причому 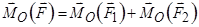 .
.
Момент сили відносно точки О дорівнює нулю, якщо точка  знаходиться на лінії дії сили (у цьому випадку
знаходиться на лінії дії сили (у цьому випадку 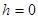 ).
).
Як приклад, знайдемо момент сили  відносно точки
відносно точки  (рис. 1.12). Проведемо радіус-вектор
(рис. 1.12). Проведемо радіус-вектор 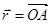 в точку прикладання сили і запишемо
в точку прикладання сили і запишемо 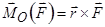 . Перенесемо радіус-вектор
. Перенесемо радіус-вектор 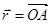 та силу
та силу  в одну точку (точку
в одну точку (точку 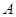 ) і повернемо найкоротшим шляхом радіус-вектор до сили.
) і повернемо найкоротшим шляхом радіус-вектор до сили.
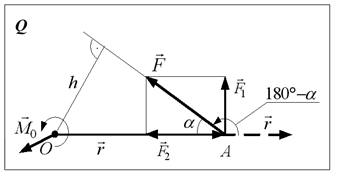
Рис. 1.12
Цей поворот показано на рис. 1.1.2 Момент буде напрямлений на читача. Такий самий результат можна отримати швидше, використовуючи “правило гвинта” відносно напряму обертання (показано на рис. 1.12), яке намагається здійснити сила  відносно точки
відносно точки  . Модуль моменту
. Модуль моменту 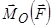 можна вирахувати такими способами. По-перше, можна використати формулу для модуля векторного добутку, а саме:
можна вирахувати такими способами. По-перше, можна використати формулу для модуля векторного добутку, а саме:
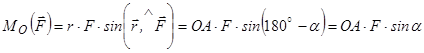 .
.
По-друге, можна також використати формулу, 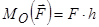 , де плече сили
, де плече сили 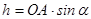 . По-третє, можна розкласти силу
. По-третє, можна розкласти силу  на складові
на складові 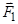 та
та 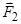 . Маємо:
. Маємо:
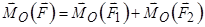 ,
,
де 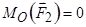 .
.
Тоді 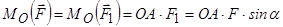 .
.
Зазначимо, що момент сили відносно точки – це вектор, який характеризується напрямом та величиною (модулем), тобто момент сили відносно точки знака не має і свідчити, що він є додатний чи від’ємний не можна (знак має проекція вектора на вісь).
Моментом сили відносно осі називають проекцію на цю вісь моменту сили відносно будь-якої точки на осі (рис. 1.13), тобто
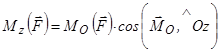 . (1.5)
. (1.5)
|
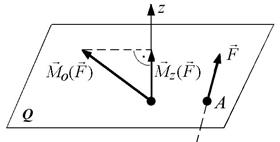
Рис. 1.13
Приклад 1.1. Знайти момент сили 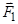 відносно осі
відносно осі 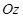 (рис. 1.14).
(рис. 1.14).
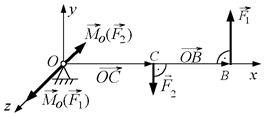
Рис. 1.14
Для цього спочатку знайдемо момент сили 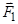 відносно якої-небудь точки на осі. Доцільно за таку точку прийняти точку
відносно якої-небудь точки на осі. Доцільно за таку точку прийняти точку  .
.
Маємо
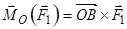 ,
,
де 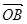 – вектор, проведений з точки
– вектор, проведений з точки 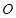 в точку
в точку 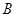 . Момент
. Момент 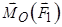 спрямований перпендикулярно до площини, в якій знаходяться ці вектори (тобто площини
спрямований перпендикулярно до площини, в якій знаходяться ці вектори (тобто площини 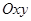 ), в бік, звідки обертання тіла, яке намагається здійснити сила
), в бік, звідки обертання тіла, яке намагається здійснити сила 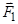 , видно проти ходу годинникової стрілки, тобто вздовж осі
, видно проти ходу годинникової стрілки, тобто вздовж осі 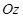 .
.
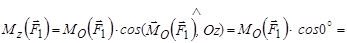
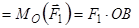 .
.
Аналогічно знаходимо, що момент сили 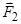 спрямований у бік, протилежний осі
спрямований у бік, протилежний осі 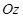
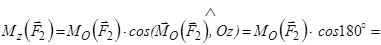
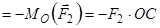 .
.
Цей результат можна узагальнити і сформулювати так: момент сили відносно осі є додатним, якщо з кінця осі обертання тіла, яке намагається здійснити сила, видно проти ходу годинникової стрілки. З цього приводу зробимо деякі зауваження. У разі визначення знака моменту сили відносно осі обов’язково требарозглядати обертання тіла з кінця осі. Річу тому, що вісь 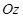 може бути спрямована і від читача, зокрема, це має місце в задачах, де осі розташовані так, як показано на рис. 1.15. Це зумовлено тим, що при розв’язанні задач використовують “праву” систему координат, тобто, якщо дивитися з кінця осі, то наступна вісь повинна бути розташована праворуч від попередньої осі. Так, якщо дивитися з кінця осі
може бути спрямована і від читача, зокрема, це має місце в задачах, де осі розташовані так, як показано на рис. 1.15. Це зумовлено тим, що при розв’язанні задач використовують “праву” систему координат, тобто, якщо дивитися з кінця осі, то наступна вісь повинна бути розташована праворуч від попередньої осі. Так, якщо дивитися з кінця осі 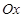 (рис. 1.15), то наступна вісь
(рис. 1.15), то наступна вісь 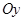 повинна бути розташована праворуч від попередньої осі
повинна бути розташована праворуч від попередньої осі 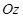 . Це означає, що вісь
. Це означає, що вісь 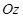 напрямлена від читача (рис. 1.15). Зазвичай в плоскій системі сил вісь
напрямлена від читача (рис. 1.15). Зазвичай в плоскій системі сил вісь 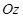 взагалі не зображується. У цьому випадку проекція вектора
взагалі не зображується. У цьому випадку проекція вектора 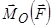 на вісь
на вісь 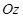 буде від’ємною, а саме:
буде від’ємною, а саме:
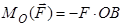 ,
,
хоча читач бачить обертання, яке намагається здійснити сила 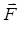 , проти ходу годинникової стрілки (треба дивитися з кінця осі). Тому доцільно при визначенні знака моменту сили відносно осі використати “правило гвинта”.
, проти ходу годинникової стрілки (треба дивитися з кінця осі). Тому доцільно при визначенні знака моменту сили відносно осі використати “правило гвинта”.
Рис. 1.15
Так, для визначення знака проекції  треба встановити напрям моменту
треба встановити напрям моменту  , що легко зробити за “правилом гвинта”, враховуючи напрям обертання, яке намагається здійснити сила
, що легко зробити за “правилом гвинта”, враховуючи напрям обертання, яке намагається здійснити сила 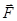 відносно точки
відносно точки 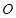 (осі
(осі 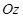 ). Цей момент спрямований проти напряму осі
). Цей момент спрямований проти напряму осі 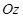 , тому момент сили відносно осі має від’ємне значення. Найпростіше безпосередньо порівняти напрям переміщення гвинта вздовж осі
, тому момент сили відносно осі має від’ємне значення. Найпростіше безпосередньо порівняти напрям переміщення гвинта вздовж осі 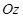 при обертанні тіла під дією сили
при обертанні тіла під дією сили 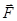 з напрямом осі
з напрямом осі 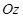 . У даному випадку вони протилежні, тобто проекція моменту на вісь є від’ємною. Якщо вісь, відносно якої обчислюють момент, та сила не взаємно перпендикулярні доцільно використати “робоче правило обчислення моменту сили відносно осі”. За цим правилом, для обчислення моменту сили відносно осі, наприклад
. У даному випадку вони протилежні, тобто проекція моменту на вісь є від’ємною. Якщо вісь, відносно якої обчислюють момент, та сила не взаємно перпендикулярні доцільно використати “робоче правило обчислення моменту сили відносно осі”. За цим правилом, для обчислення моменту сили відносно осі, наприклад 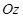 (рис. 1.16), силу спочатку проектують на площину
(рис. 1.16), силу спочатку проектують на площину 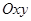 , перпендикулярну до осі
, перпендикулярну до осі 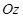 , а далі обчислюють проекцію на цю вісь моменту проекції сили
, а далі обчислюють проекцію на цю вісь моменту проекції сили 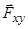 відносно точки
відносно точки 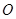 — перетину осі
— перетину осі 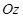 з площиною
з площиною 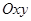 .
.
Момент сили відносно осі дорівнює нулю, якщо сила і вісь знаходяться в одній площині.
Приклад 1.2. Знайти момент сили 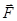 , прикладеної до пластини AOCD і розміщеної у площині, паралельній
, прикладеної до пластини AOCD і розміщеної у площині, паралельній 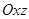 , відносно осі
, відносно осі 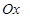 (рис. 1.17, а).
(рис. 1.17, а).
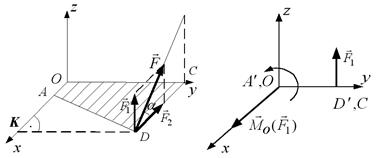
| а) | б) |
Рис. 1.17
Згідно робочого правила для знаходження моменту 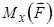 треба спроектувати силу
треба спроектувати силу 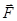 на площину
на площину 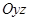 , перпендикулярну до осі
, перпендикулярну до осі 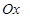 (рис. 1.17, б). При цьому пластина
(рис. 1.17, б). При цьому пластина 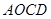 проектується, як зображено на рис. 1.17, б, у відрізок
проектується, як зображено на рис. 1.17, б, у відрізок  .Внаслідок проектування виділяється вектор
.Внаслідок проектування виділяється вектор 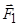 , який є складовою сили
, який є складовою сили 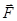 (
(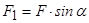 ). Точка
). Точка 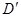 є проекцією точки
є проекцією точки 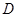 , точка А¢ є проекцією точки А. Далі за відомою методикою знаходимо проекцію на вісь
, точка А¢ є проекцією точки А. Далі за відомою методикою знаходимо проекцію на вісь 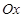 моменту сили
моменту сили 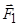 відносно точки
відносно точки 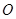 — перетину осі
— перетину осі 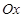 з площиною
з площиною  . За “правилом гвинта” цей вектор напрямлений вздовж осі
. За “правилом гвинта” цей вектор напрямлений вздовж осі  (на читача), тобто момент сили відносно осі є додатним. Далі обчислюємо модуль моменту сили відносно осі:
(на читача), тобто момент сили відносно осі є додатним. Далі обчислюємо модуль моменту сили відносно осі:
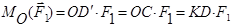 .
.
Отже,
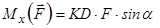 .
.
Обчислення можна спростити, якщо спочатку розкласти силу 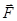 на дві складові
на дві складові 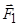 та
та 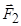 . Сила
. Сила 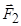 та вісь
та вісь 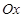 знаходяться в одній площині
знаходяться в одній площині 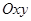 , тому
, тому 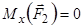 . Для обчислення моменту
. Для обчислення моменту 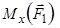 можна використати відрізок
можна використати відрізок 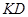 , який є найкоротшою відстанню від точки прикладання сили
, який є найкоротшою відстанню від точки прикладання сили 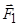 до осі
до осі 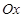 . Перевагою розкладання сили на складові є те, що в цьому випадку, як правило, не треба виконувати допоміжне проектування на площину, перпендикулярну до осі.
. Перевагою розкладання сили на складові є те, що в цьому випадку, як правило, не треба виконувати допоміжне проектування на площину, перпендикулярну до осі.
Парою сил називають систему прикладених до одного тіла двох сил, що рівні за модулем і протилежні за напрямом, лінії дії яких не збігаються (рис. 1.18).Пару сил характеризують моментом 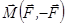 .
.
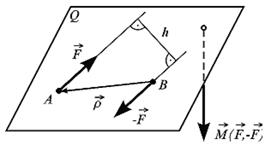
Рис. 1.18
Площину  , в якій знаходяться сили
, в якій знаходяться сили  та
та  , називають площиною дії пари сил. Найкоротша відстань
, називають площиною дії пари сил. Найкоротша відстань 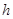 між лініями дії сил
між лініями дії сил 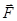 та
та 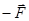 називають плечем пари.
називають плечем пари.
Момент пари дорівнює:
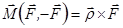 . (1.6)
. (1.6)
Якщо момент кожної окремоїсили, що утворюють пару, відносно деякої точки 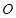 залежить від розташування точки, то момент пари сил від розташування цієї точки не залежить.
залежить від розташування точки, то момент пари сил від розташування цієї точки не залежить.
Момент пари сил напрямлений перпендикулярно до площини дії пари в той бік, звідки обертання, яке намагається здійснити пара сил, видно проти ходу годинникової стрілки (“правило гвинта”). Вектор 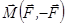 може бути зображений у будь-якій точці фігури. На рис. 1.18 вектор
може бути зображений у будь-якій точці фігури. На рис. 1.18 вектор 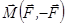 нап-
нап-
рямлений вниз перпендикулярно до площини 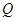 .
.
Модуль моменту пари дорівнює
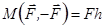 . (1.7)
. (1.7)
Дія пари сил на тіло не зміниться в разі такої зміни сили та плеча пари, за якої момент пари залишається незмінним за напрямом та величиною.
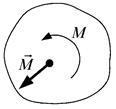
Умовне зображення моменту пари зображено на (рис. 1.19), де 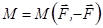 – модуль моменту пари, а стрілкою позначений напрям обертання, яке намагається здійснити пара сил. Наведеній на рис. 1.19 парі сил відповідає вектор моменту пари
– модуль моменту пари, а стрілкою позначений напрям обертання, яке намагається здійснити пара сил. Наведеній на рис. 1.19 парі сил відповідає вектор моменту пари 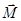 , напрямлений на читача.
, напрямлений на читача.
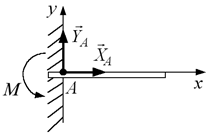
Пара сил має місце в опорі, яку називають жорстким защемленням (рис. 1.20). Тут невідомими є сили 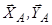 та момент
та момент  , що виникає в опорі.
, що виникає в опорі.
| 
|
| Рис. 1.19 | Рис. 1.20 |