Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Умови рівноваги систем сил
|
|
Головним вектором системи сил називають векторну суму сил системи. Головним моментом системи сил відносно деякої точки називають векторну суму моментів сил системи відносно цієї точки:
; 
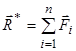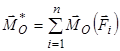. (2.1)
Для рівноваги будь-якої системи сил необхідно й достатньо, щоб головний вектор і головний момент системи сил відносно деякої точки 
дорівнювали нулеві:
; 
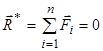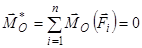. (2.2)
Аналітичні умови рівноваги просторової системи сил в координатній формі мають вигляд:
; 
; 
;
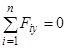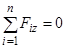(2.3)
; 
; 
.
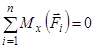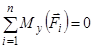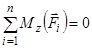Аналітичні умови рівноваги збіжної системи сил (системи сил, лінії дії яких перетинаються в одній точці) мають вигляд:
; 
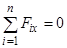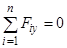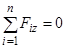; . (2.4)
Аналітичні умови рівноваги плоскої системи сил (системи сил, які знаходяться в одній площині, наприклад,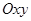 
) мають вигляд
; 
; 
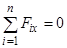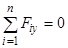, (2.5)
або
; 
; 
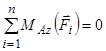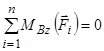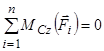, (2.6)
де точки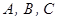 
не лежать на одній прямій, або
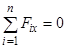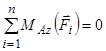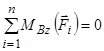; ; , (2.7)
де вісь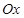 
не перпендикулярна до лінії 
.
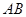Аналітичні умови рівноваги системи паралельних сил (системи сил, які паралельні, наприклад, осі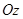 
) мають вигляд:
; 
; 
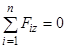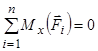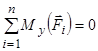. (2.8)
Умовам рівноваги (2.4) можна надати інший зміст, якщо врахувати, що збіжна система сил еквівалентна одній силі – рівнодійній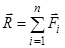 
. Таким чином, умову рівноваги збіжної системи сил можна записати у вигляді:
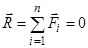. (2.9)
Вираз (2.9) означає, що багатокутник збіжних сил за умови рівноваги є замкненим. За графічним методом розв’язання задачі напрями і модулі невідомих сил визначаються з аналізу замкненого багатокутника сил.
Аналітичний метод розв’язання задачі пов’язаний з проектуванням сил на осі. Проекція сили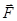 
(рис. 2.1, а) на вісь 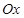з ортом 
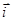визначається таким чином:
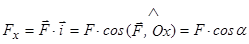. (2.10)
Для визначення кута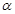 
між силою та віссю їх необхідно перенести в одну точку. Якщо не заданий кут 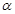між силою і віссю, а відомим є кут 
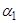між прямими, вздовж яких напрямлені сила та вісь (рис. 2.1, б; 2.1, в), то проекція сили на вісь дорівнює:
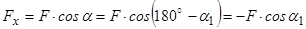. (2.11)
Проекція сили на вісь є від’ємною, коли кут між силою й віссю є тупим. Тому проектування сили на вісь можна спростити, якщо поступати таким чином. У випадках, яким відповідають рис. 2.1, б; 2.1, в, знак проекції визначається безпосередньо з рисунка, це “мінус”, а модуль сили множиться на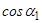 
, тобто відразу записують
.
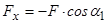х
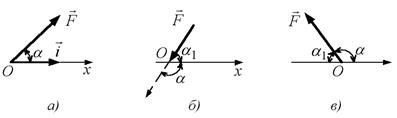
Рис. 2.1
Проекція сили на вісь дорівнює нулеві, коли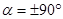 
, тобто вектор 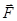і вісь взаємно перпендикулярні.
У більш загальному випадку проекції сили 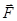на осі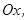 
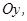
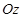(рис. 2.2, а) визначають наступним чином:
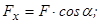
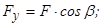
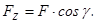(2.12)
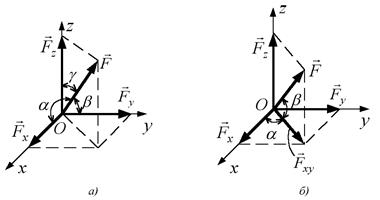
Рис. 2.2
Якщо положення вектора сили задається так, як показано на рис. 2.2, б (кут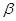 
заданий в площині, що перпендикулярна до площини 
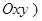, то проекції сили на осі мають вигляд
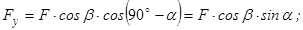(2.13)
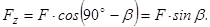
Тобто у разі проектування сили на осі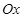 
та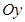 
силу спочатку проектують на площину 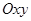, отримують вектор 
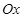, далі цей вектор проектують на осі і 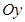в площині .
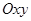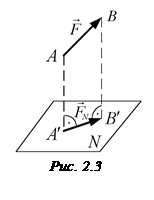
Проекцією вектора 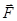на площину 
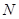(рис. 2.3) є вектор 
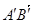(тобто 
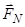), початком і кінцем якого відповідно є проекції на площину 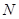початку і кінця вектора .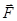