Плоска система сил

Приклад 3.6. Знайти реакції опор балки 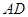, на яку діє сила 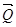і до якої підвішений вантаж вагою 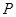(риc. 3.14, а).

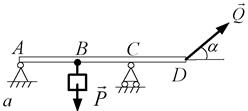
а)

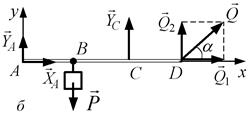
б)

Рис. 3.14

Розв'язання. Зобразимо відомі сили: 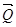, вагу 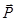та невідомі реакції опор (шарніра 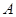та котка 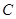), прикладені до балки. Будемо розглядати рівновагу системи: балка – нитка – вантаж. Для плоскої системи сил зобразимо тільки ті сили, що знаходяться в площині рисунка, тобто тільки дві реакції шарнір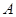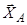а : та 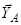. Реакція котка 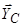спрямована по нормалі до поверхні балки. Маємо три невідомі сили і три аналітичні умови рівноваги для довільної плоскої системи сил. Отже задача має розв’язок.

Запишемо перші два рівняння рівноваги:

;

.

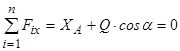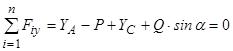Більш детально розглянемо третє рівняння – рівняння моментів відносно осі, спрямованої перпендикулярно до площини 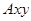. Ця вісь напрямлена на читача і може проходити через будь-яку точку плоскої фігури. Цю точку доцільно вибрати таким чином, щоб через неї проходило якомога більше ліній дії невідомих сил (момент цих сил відносно даної точки дорівнює нулю), – це спрощує запис третього рівняння рівноваги. В даній задачі таких точок дві: точка 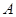(через неї проходять лініїдії реакцій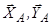

лінії

) та 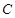(через неї проходять лінії дії реакцій 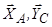). Візьмемо точку 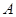, тобто будемо розглядати вісь 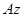, яка напрямлена на читача (звичайно вісь 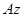не зображують). Сили 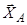, 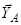перетинають вісь 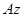, тому моменти цих сил відносно осі 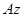дорівнюють нулеві.

Знайдемо. Встановлюємо, що зміщення гвинта, яке зумовлене дією сили, спрямоване від читача, а внаслідок того, що вісь, навпаки, спрямована на читача, отримаємо від’ємне значення моменту. Модуль моменту дорівнює добутку сили Р на плече.

Отже

.

Аналогічно знаходимо:

.

Для визначення моменту 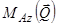розкладемо силу 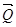на складові 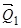та 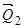. Складова 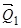перетинає вісь 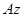, отже її момент відносно осі 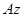дорівнює нулеві. Момент складової 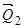(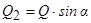) дорівнює:

.

Остаточно маємо:

.

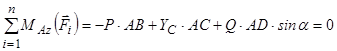Далі знаходимо: ;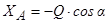

;

.

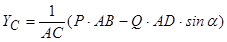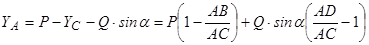Приклад 3.7. Знайти реакції опори 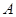невагомої балки, якщо відома вага вантажа 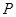(рис. 3.15, а).

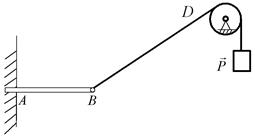
а)

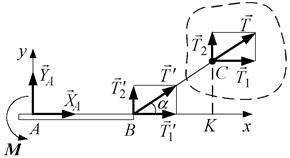
б)

Рис. 3.15

Розв'язання. У жорсткому защемленні в точці 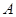мають місце реакції 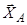, 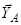та момент 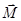. Щоб виключити з розгляду реакції блока, перерізаємо нитку в точці 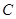і будемо розглядати рівновагу системи: балка, частина нитки 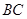. Звільняємося від в’язей і вводимо реакції в’язей 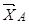, , 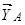, 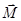також вводимо натяг нитки 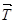(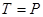) (рис. 3.15, б). Рівняння рівноваги мають вигляд:

;

.

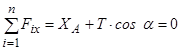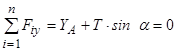Пара сил в ці рівняння не входить, тому що векторна сума сил, що утворюють пару, дорівнює нулеві.

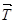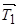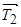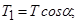
Для запису рівняння моментів, розкладемо силу на складові та ( 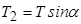) і знайдемо.

.

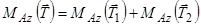Отримаємо

.

Далі знаходимо

.

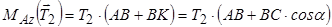Отже

.

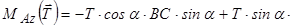
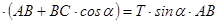Бачимо, що момент 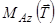не залежить від вибору точки 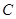(на відрізку 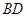від точки до точки 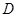– дотику нитки до блока). Це і слід було чекати, тому що сила є ковзним вектором, і ми могли перенести силу 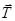в будь-яку точку на лінії

її дії, не змінюючи стану системи, що розглядається. Тому доцільно було б нитку перерізати не в точці С, а в точці , (тобто перенести точку С в точку). B (рис. 3.15, б).

Тоді отримаємо:

.

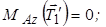
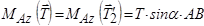У той же час ці обчислення показують, що при розв’язанні задачі потрібно чітко визначити, де конкретно прикладена кожна з сил, тобто рівновага якої системи розглядається.

Остаточно третє рівняння рівноваги має вигляд:

.

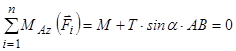Розв’язуючи отриману систему рівнянь з урахуванням 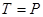, знаходимо:

; ; .

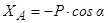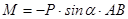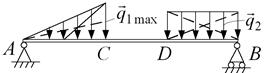
Приклад 3.8. Знайти реакції опор невагомої балки 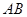, на яку діють розподілені сили з інтенсивністю q_1max =10 Н/м;
q ₂ = 20 Н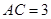/м; 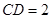м; м; 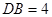м (рис.3.16, а).

а)

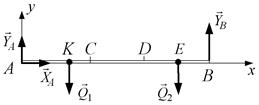
б)

Рис. 3.16