Збіжна система сил

3.

РОЗВ’ЯЗАННЯ ЗАДАЧ СТАТИКИ

Методика розв’язання задач статики

1. Вибрати тіло (систему тіл), рівновага якого буде розглядатися. Звичайно – це тіло, до якого прикладені задані сили та сили, які треба знайти.

2. Зобразити активні сили, які задані за умовою задачі.

3. Визначити кількість та тип в’язей. Далі за аксіомою про звільнення від в’язей звільнити тіло від них та ввести реакції в’язей, що прикладені до точок тіла.

На цьому закінчується етап зображення сил. Зображуються тільки зовнішні сили, що діють на вибране тіло чи систему тіл (внутрішні сили в твердому тілі утворюють зрівноважену систему сил, тобто систему сил, еквівалентну нулеві).

4. При графічному методі розв’язання задачі треба побудувати замкнені багатокутники сил і моментів; при аналітичному – записати аналітичні умови рівноваги.

При графічному методі конкретний напрям реакції в’язей, тобто стрілку на рисунку, визначають в процесі побудови багатокутника сил. При аналітичному методі конкретнийнапрям реакції, тобто стрілку, задають довільно.на початку розв’язання задачі.

При аналітичному методі треба перевірити відповідність кількості невідомих реакцій кількості рівнянь рівноваги. Задача повинна бути статично визначеною.

5. При графічному методі геометрично знаходять напрями та модулі невідомих сил. При аналітичному методі розв’язують систему рівнянь відносно вказаних невідомих. Якщо після розв’язання відповідна сила має додатне значення, то це означає, що відповідна сила має напрям, показаний на рисунку, якщо від’ємне – то протилежне зображеному.

Збіжна система сил

Приклад 3.1. На рис. 3.1 зображені стрижн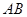і і 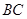, з’єднані між собою та зі стелею за допомогою шарнірів. До шарніра на невагомій нитці підвішений вантаж вагою 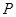. Знайти зусилля в стрижнях.

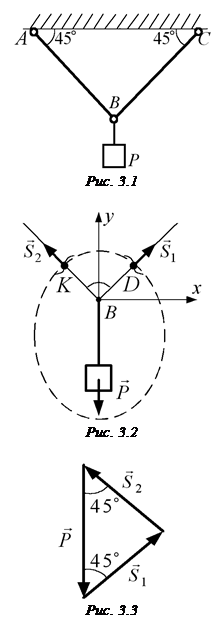Розв’язання.

Графічний метод розв’я-зання.Зображуємо силу 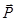, що прикладена до вантажа. Розріжемо стрижні 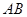та 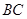, тому що в них потрібно визначити зусилля.

При цьому внутрішні сили в них переводять у зовнішні. Стрижні можна перерізати в будь-якому місці. У місці розрізу зображають реакцію стрижня, яка напрямлена вздовж нього (місця розрізів 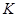, 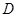показані на рис. 3.2). Нитку не перерізають, тому що знаходити натяг нитки не треба.

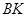Таким чином, будемо розглядати систему, що складається з таких тіл: вантаж, нитка, шарнір , частини стрижнів та 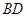. Ця система обведена на рис. 3.2. З деякої точки відкладемо відому силу 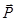(рис. 3.3). Далі з кінця вектора 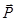відкладаємо силу, паралельну до лінії дії реакції 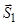стрижня, наприклад 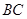, а з початку вектора 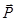силу, паралельну до лінії дії реакцій 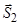стрижня 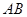. Отримаємо замкнений трикутник сил, де сили 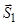та 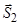є зусиллями в стрижнях 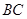та 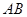відповідно. Напрями векторів ми розставляємо по колу за правилом векторної суми. При цьому в процесі побудови трикутника ми визначились із конкретним напрямом цих сил. Тепер їх можна перенести на рис. 3.2. Сили доцільно зображати так, щоб початок відповідного вектора був у місці перерізу. З геометрії конструкції визначаємо кути між лініями дії сил. Далі, аналізуючи отриманий прямокутний трикутник, знаходимо модулі сил: відповідних стрижнів:

.

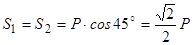Аналітичний метод розв’язання.

У цьому випадку реакції стрижнів 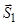та 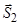зображують відразу. Це пояснюється тим, що далі буде проектування векторів на осі, а це потребує наявності вектора на рисунку. При цьому реакції 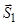та 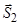можна зображати напрямленими вздовж відповідних стрижнів у будь-якому напрямі.

Приймемо, що сили 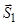та 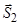напрямлені від місць перерізів, тобто так, як вже зображено на рис. 3.2.

Введемо систему координат 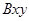. Система координат може

бути розташована довільно, але доцільним є таке її розташування, коли початок системи координат знаходиться в точці перетину сил, а осі були напрямлені так, щоб проектування сил здійснювалося найпростішим чином.

Так як всі сили розташовані в площині рисунка, достатньо ввести лише дві осі 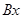та .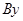

ДЗаписуємо рівняння рівноваги:

;

.

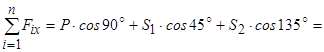
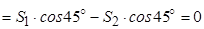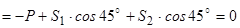З першого рівняння знаходимо 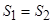. З другого рівняння знаходимо зусилля в стрижнях

.

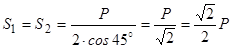Отриманий знак “плюс” означає, що реальні напрями сил 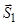та 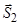збігаються із зображеними на рис. 3.2.

Розглянемо тепер наведену задачу в такому трактуванні: необхідно знайти зусилля в стeрижнях та натяг нитки.

Необхідність знаходження натягу нитки означає, що нитку необхідно перерізати (аналогічно стрижням), але етап розв’язання задачі, на якому це треба зробити, можна вибрати по-різному. По-перше, треба відзначити, що при одночасному перерізі стрижнів і нитки та одночасному знаходженні трьох невідомих це зробити буде неможливо. 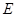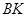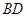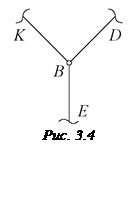Справді, припустимо, що одночасно перерізана нитка в точці та стрижні і розглядається рівновага системи, що складається з тіл: частина стрижня , частина стрижня , шарнір , частина нитки 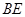(рис. 3.4). Усі три сили невідомі. Знайти необхідні зусилля неможливо. Тому ця задача може бути розв’язана наступними шляхами.