
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Просторова система сил
|
|
Приклад 3.11. До коловорота  під прямим кутом жорстко прикріпленоий стрижень балку
під прямим кутом жорстко прикріпленоий стрижень балку  , до якоїго прикладено розподілене навантаження
, до якоїго прикладено розподілене навантаження 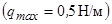 . Коловорот утримується в рівновазі силою
. Коловорот утримується в рівновазі силою 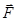 (яка паралельна площині
(яка паралельна площині 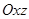 ), прикладеною в точці
), прикладеною в точці 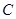 під кутом
під кутом 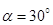 до
до 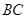 . Визначити величину сили
. Визначити величину сили 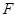 (рис. 3.19, а).
(рис. 3.19, а).
Розв’язання. Розподілене навантаження замінимо зосередженою силою 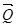 , яку прикладемо у точці
, яку прикладемо у точці 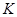 балки
балки 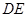 на відстані
на відстані 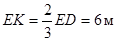 (бо центр ваги трикутника
(бо центр ваги трикутника 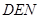 , по якому розподілена сила
, по якому розподілена сила 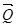 , знаходиться на відстані
, знаходиться на відстані 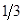
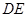
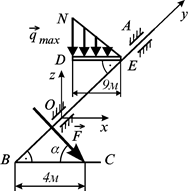
а)
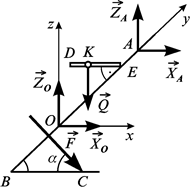
б)
Рис. 3.19
від вершини прямого кута 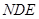 ). Величина сили
). Величина сили 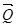 визначається площею фігури, по якій вона розподілена (D DEN). Отже,
визначається площею фігури, по якій вона розподілена (D DEN). Отже,
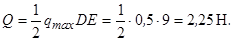
Аналізуємо сили: активні сили  і
і  прикладені до балки та коловорота відповідно; реакції опор (циліндричних підшипників
прикладені до балки та коловорота відповідно; реакції опор (циліндричних підшипників 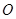 і
і 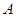 ) прикладені до коловорота. Отже, доцільно розглянути рівновагу системи тіл: коловорот і балка, до якої прикладена просторова система сил
) прикладені до коловорота. Отже, доцільно розглянути рівновагу системи тіл: коловорот і балка, до якої прикладена просторова система сил 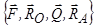 . Реакції підшипників (рис. 3.19, б)
. Реакції підшипників (рис. 3.19, б) 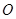 і
і 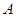 подамо у вигляді двох складових, перпендикулярних до осі обертання
подамо у вигляді двох складових, перпендикулярних до осі обертання 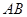 :
:
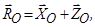
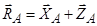 .
.
Маємо 5 невідомих сил: 4 реакції в’язей та сила 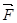 . Для просторової системи сил можна записати 6 рівнянь рівноваги, тобто задача є статично визначеною.
. Для просторової системи сил можна записати 6 рівнянь рівноваги, тобто задача є статично визначеною.
Шуканою силою є сила 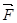 , тому доцільно записати лише те рівняння рівноваги, в яке увійдуть відома сила
, тому доцільно записати лише те рівняння рівноваги, в яке увійдуть відома сила 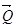 і невідома сила
і невідома сила 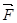 . Так як лінії дії реакцій підшипників
. Так як лінії дії реакцій підшипників 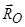 і
і 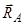 перетинають вісь
перетинають вісь 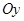 , то момент цих сил відносно цієї осі дорівнює нулеві. Отже, в рівняння моментів сил відносно осі
, то момент цих сил відносно цієї осі дорівнює нулеві. Отже, в рівняння моментів сил відносно осі 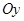 ввійдуть лише сили
ввійдуть лише сили 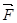 і
і 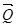 .
.
Знайдемо момент сили 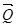 відносно осі
відносно осі 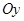 . Для цього спочатку знайдемо момент сили
. Для цього спочатку знайдемо момент сили 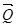 відносно якої-небудь точки на осі. Доцільно за таку точку вибрати точку
відносно якої-небудь точки на осі. Доцільно за таку точку вибрати точку 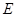 . Далі знаходимо вектор
. Далі знаходимо вектор  , який спрямований в бік, звідки обертання тіла, яке намагається здійснити сила
, який спрямований в бік, звідки обертання тіла, яке намагається здійснити сила 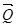 , видно проти ходу годинникової стрілки, тобто на читача (протилежно напрямку осі
, видно проти ходу годинникової стрілки, тобто на читача (протилежно напрямку осі 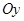 ) (рис. 3.20). (Доцільним є також використання “правила гвинта”). Тоді
) (рис. 3.20). (Доцільним є також використання “правила гвинта”). Тоді
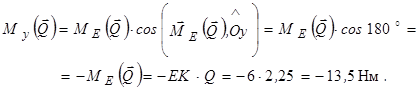
Далі знайдемо момент сили 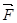 відносно цієї ж осі. Так як вектор сили
відносно цієї ж осі. Так як вектор сили 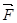 за умовою задачі лежить в площині
за умовою задачі лежить в площині 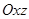 , то сила
, то сила 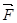 і вісь
і вісь 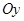 взаємно перпендикулярні і вектор моменту цієї сили доцільно знаходити відносно точки
взаємно перпендикулярні і вектор моменту цієї сили доцільно знаходити відносно точки 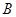 . Вектор
. Вектор 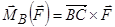 спрямований в бік, звідки обертання тіла, яке намагається здійснити сила
спрямований в бік, звідки обертання тіла, яке намагається здійснити сила 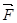 , видно за ходомходом годинниковоїюї стрілкииою, тобто вздовж осі
, видно за ходомходом годинниковоїюї стрілкииою, тобто вздовж осі 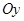 (рис. 3.21).
(рис. 3.21).
Рис.3.20 Тоді

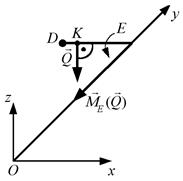 Рис. 3.20
Рис. 3.20
| 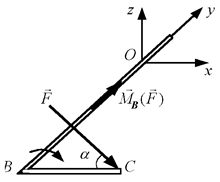 Рис. 3.21
Рис. 3.21
|
Рівняння рівноваги системи сил 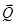 і
і 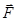 відносно осі
відносно осі 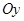 запишеться так:
запишеться так:
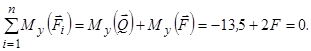
Звідси знаходимо 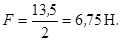
Приклад 3.12. Однорідна трикутна пластина вагою 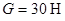 , яка може
, яка може
обертатися навколо осі 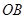 , утримується в рівновазі ниткою
, утримується в рівновазі ниткою 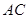 , кут між
, кут між
якою та площиною пластини дорівнює 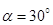 . Нитка, яка прикріплена до пластини в точці пластини в точці D (AD = DO), перекинута через блок
. Нитка, яка прикріплена до пластини в точці пластини в точці D (AD = DO), перекинута через блок  і перекинута через блок
і перекинута через блок  іутримує вантаж
іутримує вантаж
вагою 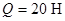 . Визначити реакції сферичного
. Визначити реакції сферичного
шарніра О та петліцилін-дричної петлі 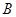 , якщо ОА = 5 см; ОВ = 3 см; АВ = 4 см (рис. 3.22, а).
, якщо ОА = 5 см; ОВ = 3 см; АВ = 4 см (рис. 3.22, а).
Розв’язання. Оскільки за умовою задачі пластина однорідна, силу 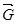 прикладемо в
прикладемо в
центрі ваги пластини (рис. 3.22, б). Переріжемо нитку 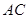 в точці
в точці 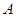 та введемо натяг нитки
та введемо натяг нитки 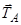 . Щоб виключити з розгляду реакцію блока
. Щоб виключити з розгляду реакцію блока 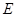 , переріжемо нитку, яка
, переріжемо нитку, яка
утримує вантаж, у точці 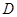 та введемо натяг нитки
та введемо натяг нитки 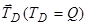 . Зауважимо, що
. Зауважимо, що
вектор натягу нитки слід напрямляти від тіла, рівновага якого розглядається. У даному випадку таким тілом є
пластина – саме до неї прикладені шукані реакції опор: реакція сферичного шарніра О та циліндричної петлі B. Реакція сферичного шарніра О дорівнює:
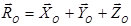 ,
,
а циліндричної петлі B:
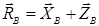 .
.
Пояснимо відсутність складової 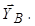 Річ у тім, що петля також обмежує рух пластини в напрямі осі
Річ у тім, що петля також обмежує рух пластини в напрямі осі 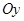 , тобто реакція
, тобто реакція 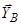 може мати місце. Але методами теоретичної механіки розділити реакції
може мати місце. Але методами теоретичної механіки розділити реакції 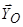 та
та 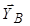 не можна (в усі рівняння рівноваги входить їх сума). Тому в задачах у таких випадках зображується тільки одна з них (звичайно — це реакція в сферичному шарнірі). Саме це й зроблено.
не можна (в усі рівняння рівноваги входить їх сума). Тому в задачах у таких випадках зображується тільки одна з них (звичайно — це реакція в сферичному шарнірі). Саме це й зроблено.
Таким чином, невідомими є 6 складових реакцій в’язей: 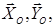
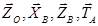 . Задача статично визначена.
. Задача статично визначена.
Для полегшення запису рівнянь рівноваги розкладемо силу 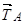 , що лежить у площині прямокутного трикутника
, що лежить у площині прямокутного трикутника 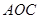 , на складові:
, на складові:
| а) | 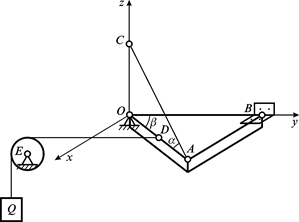
|
| б) | 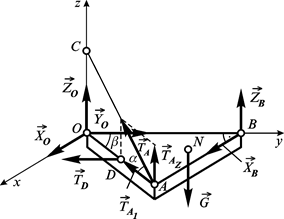
|
Рис. 3.22
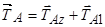 ;
; 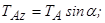
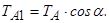
Далі записуємо рівняння рівноваги.
Перші три рівняння – це проекції головного вектора сил на координатні осі:
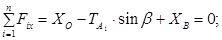 (3.1)
(3.1)
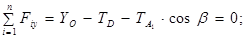 (3.2)
(3.2)
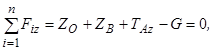 (3.3)
(3.3)
де 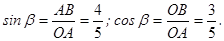
Записуючи рівняння моментів, врахуємо що в них будуть відсутні сили 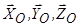 ,. Тбо їхні лінії дії проходять через початок системи координат
,. Тбо їхні лінії дії проходять через початок системи координат 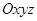 – точку
– точку 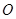 і, таким чином, перетинають всі три осі. Отже, не створюють моментів відносно жодної з осей.
і, таким чином, перетинають всі три осі. Отже, не створюють моментів відносно жодної з осей.
Записуючи проекції моментів на вісьрівняння моментів відносно осі  , відкидаємо додатково сили, лінії дії яких паралельні осі
, відкидаємо додатково сили, лінії дії яких паралельні осі 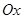 , або її перетинають – це сили
, або її перетинають – це сили 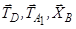 . А для решти сил
. А для решти сил 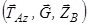 записуємо:
записуємо:
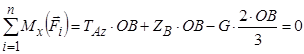 . (3.4)
. (3.4)
При визначенні моментів відносно осі 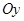 відкидаємо силу
відкидаємо силу 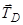 (паралельну осі
(паралельну осі 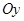 ) та сили
) та сили 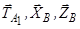 (перетинають вісь
(перетинають вісь 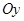 ). Для решти сил
). Для решти сил 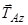 і
і 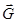 маємо:
маємо:
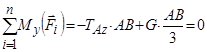 . (3.5)
. (3.5)
Аналогічно для осі 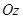 відкидаємо сили
відкидаємо сили 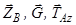 (паралельні осі
(паралельні осі 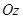 ),
), 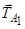 (перетинає вісь
(перетинає вісь  ). Для решти сил
). Для решти сил 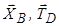 маємо:
маємо:
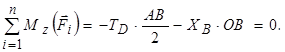 3.6)
3.6)
Розв’язуємо отриману систему рівнянь. Із рівняння (3.6) знаходимо
 .
.
З рівняння (3.5) знаходимо:
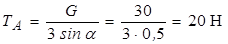 H.
H.
З рівняння (3.2) знаходимо
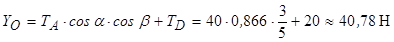 .
.
З рівняння (3.1) знаходимо
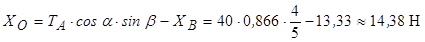 .
.
З рівняння (3.4) знаходимо
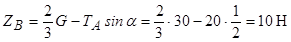 .
.
З рівняння (3.3) знаходимо
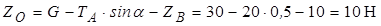 .
.
Приклад 3.13. На квадратну пластину вагою 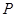 діють сили
діють сили 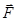 і
і 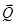 , паралельні осі
, паралельні осі 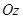 . Пластина утримується в рівновазі шістьма п’ятьма стрижнями. Визначити зусилля в стрижнях (рРис. 3.23, а).
. Пластина утримується в рівновазі шістьма п’ятьма стрижнями. Визначити зусилля в стрижнях (рРис. 3.23, а).
Розв’язання. Будемо розглядати рівновагу пластини. Прикладемо до неї силу ваги 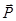 у центрі пластини. Стрижні, які підтримують пластину, відкинемо і замінимо реакціями, спрямованими вздовж них і прикладеними до пластини. Сили
у центрі пластини. Стрижні, які підтримують пластину, відкинемо і замінимо реакціями, спрямованими вздовж них і прикладеними до пластини. Сили 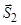 і
і 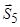 , що лежать у площинах, паралельних
, що лежать у площинах, паралельних 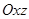 , розкладемо на складові, паралельні осям
, розкладемо на складові, паралельні осям 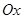 і
і 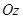 :
:
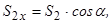
де 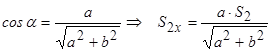 ;
;
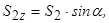
де 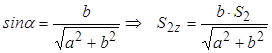 .
.
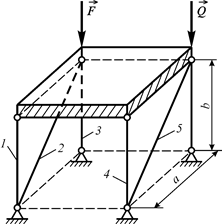
а)
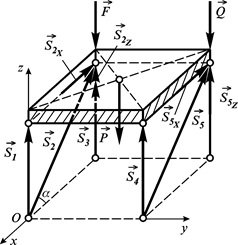
б)
Рис. 3.23
Відповідно
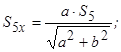
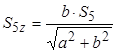 .
.
Запишемо шість рівнянь рівноваги для просторової задачі.
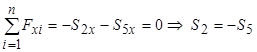 ;
;
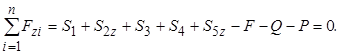 (3.7)
(3.7)
Проекція головного вектора на вісь 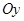 дорівнює нулеві, так як лінії дії всіх сил лежать у площинах, паралельних
дорівнює нулеві, так як лінії дії всіх сил лежать у площинах, паралельних 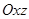 .
.
У рівнянні моментів відносно осі 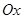 сили
сили 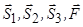 , лінії дії яких перетинають її, і силу
, лінії дії яких перетинають її, і силу 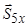 , лінія дії якої паралельна осі
, лінія дії якої паралельна осі 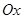 , відкидаємо. Для решти сил маємо
, відкидаємо. Для решти сил маємо
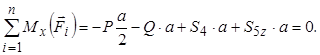 (3.8)
(3.8)
У рівнянні моментів відносно осі 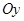 відсутні сили
відсутні сили 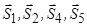 , бо їхні лінії дії перетинають цю вісь. Маємо:
, бо їхні лінії дії перетинають цю вісь. Маємо:
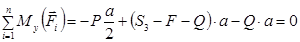 . (3.9)
. (3.9)
У рівнянні моментів відносно осі 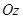 сили
сили 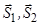 , лінії дії яких перетинають її, і сили
, лінії дії яких перетинають її, і сили 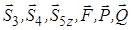 , лінії дії яких паралельні осі
, лінії дії яких паралельні осі 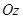 , відкидаємо. Для сили
, відкидаємо. Для сили 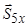 маємо
маємо
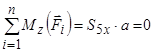 . (3.10)
. (3.10)
Розв’язавши систему рівнянь (3.7¸ 3.10), отримаємо: маємо:
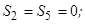
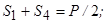
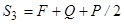 ;
; 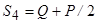 .
.
Тобто,
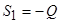 ;
; 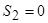 ;
; 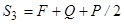 ;
;
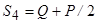 ;
; 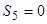 .
.