
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неможливо. Тому ця задача може бути вирішена
|
|
Перший шлях.: сСпочатку знаходимо сили 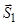 та
та 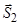 без перерізу нитки (як це було вже виконано), а далі перерізається нитка і знаходиться натяг нитки, що, в свою чергу може бути виконано двома способами. Це пояснюється тим, що після перерізу нитки ми отримаємо дві підсистеми.
без перерізу нитки (як це було вже виконано), а далі перерізається нитка і знаходиться натяг нитки, що, в свою чергу може бути виконано двома способами. Це пояснюється тим, що після перерізу нитки ми отримаємо дві підсистеми.
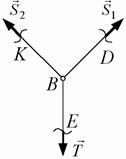
Перша підсистема (рис. 3.5, а) містить: частину стрижня 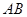 , частину стрижня
, частину стрижня 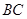 , шарнір
, шарнір  , частину нитки BE. На цю підсистему діють вже відомі сили
, частину нитки BE. На цю підсистему діють вже відомі сили 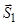 ,
, 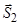 та невідома сила, яку треба визначити (натяг нитки
та невідома сила, яку треба визначити (натяг нитки 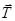 ), тобто сила, з якою відкинута частина нитки діє на частину нитки
), тобто сила, з якою відкинута частина нитки діє на частину нитки 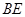 . Силу
. Силу 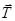 можна знайти як графічно, так і аналітично. Простіше розглянути підсистему, що
можна знайти як графічно, так і аналітично. Простіше розглянути підсистему, що
Рис.3.5 складається з вантажа та частини
нитки (рис. 3.5, б). На цю підсистему діють сили 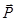 та натяг нитки
та натяг нитки 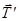 , тобто сила з якою відкинута верхня частина нитки діє на нижню. (Сили
, тобто сила з якою відкинута верхня частина нитки діє на нижню. (Сили 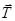 та
та 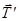 є силами дії та протидії, тому
є силами дії та протидії, тому 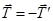 ). Згідно аксіоми про дві сили маємо
). Згідно аксіоми про дві сили маємо 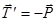 , тобто
, тобто 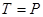 .
.
 а)
а)
| 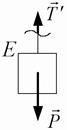 б)
б)
|
| Рис. 3.5 |
Другий шлях. Відразу розрізаємо нитку і знаходимо силу  згідно рис. 3.5, б. Далі знаходимо силу
згідно рис. 3.5, б. Далі знаходимо силу  . Після чого, аналізуючи систему, що зображена на рис. 3.5, а, знаходимо сили
. Після чого, аналізуючи систему, що зображена на рис. 3.5, а, знаходимо сили 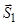 та
та 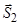 , розглядаючи силу
, розглядаючи силу 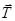 як відому.
як відому.
За кількістю обчислень усі можливі варіанти розв’язання задачі достатньо близькі. Все визначається змістом задачі.
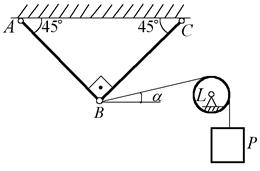
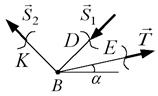
Приклад 3.2. На рис. 3.6, а зображена система тіл, аналогічна системі, зображеній на рис. 3.1, але нитка перекинута через блок 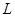 , закріплений шарнірно. Треба знайти зусилля в стрижнях.
, закріплений шарнірно. Треба знайти зусилля в стрижнях.
Розв’язання. Зобразимо відому силу 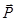 та невідомі сили
та невідомі сили 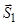 та
та 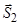 (рис. 3.6, б). Рис.3.6 6 Таким чином, будемо розглядати систему тіл: частину стрижня
(рис. 3.6, б). Рис.3.6 6 Таким чином, будемо розглядати систему тіл: частину стрижня 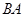 , частину стрижня
, частину стрижня 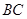 , шарнір
, шарнір 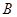 , нитку, блок
, нитку, блок 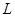 , вантаж
, вантаж 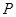 . У зв’язку з тим, що блок закріплений за допомогою нерухомого шарніра, треба ввести до розгляду реакцію шарніра
. У зв’язку з тим, що блок закріплений за допомогою нерухомого шарніра, треба ввести до розгляду реакцію шарніра 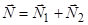 . Тоді система сил не є збіжною. Крім того, кількість невідомих сил дорівнює чотирьом, що перевищує максимальну кількість рівнянь (три) довільної плоскої системи сил. Тому необхідно змінити систему тіл, рівновага якої буде розглядатися. Для виключення із розгляду реакцій
. Тоді система сил не є збіжною. Крім того, кількість невідомих сил дорівнює чотирьом, що перевищує максимальну кількість рівнянь (три) довільної плоскої системи сил. Тому необхідно змінити систему тіл, рівновага якої буде розглядатися. Для виключення із розгляду реакцій 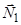 та
та  розріжемо нитку в точці
розріжемо нитку в точці  і знайдемо
і знайдемо
а)
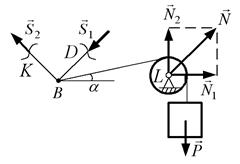
б)
Рис. 3.6
спочатку натяг нитки, тобто використаємо методику роз-в’язання, розглянуту в попередній задачі. Для цього розглянемо відкинуту систему: блок, вантаж, частину нитки (рис. 3.7, а). Силами, що на неї діють, є три сили: вага вантажу 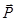 , натяг нитки
, натяг нитки 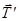 та реакція
та реакція 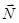 шарніра
шарніра 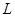 . Лінії дії двох сил
. Лінії дії двох сил 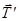 і
і 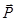 перетинаються в точці
перетинаються в точці 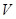 , отже, згідно теореми про три сили, реакція шарніра
, отже, згідно теореми про три сили, реакція шарніра 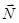 також буде проходити через
також буде проходити через
точку 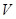 .
.
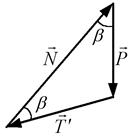
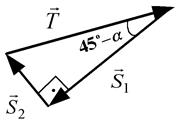
Побудуємо трикутник сил (рис. 3.8, а), з якого видно, що 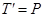 . Далі розглядається система тіл: частина стрижня
. Далі розглядається система тіл: частина стрижня 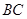 , частина стрижня
, частина стрижня 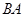 , шарнір
, шарнір 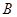 , частина нитки
, частина нитки 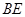 , де відомою є сила
, де відомою є сила 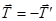 , а невідомими – сили
, а невідомими – сили 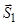 та
та 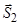 (рис. 3.7, б). Силовий трикутник на рис. 3.8, б побудований аналогічно тому, що на рис. 3.8, а.
(рис. 3.7, б). Силовий трикутник на рис. 3.8, б побудований аналогічно тому, що на рис. 3.8, а.
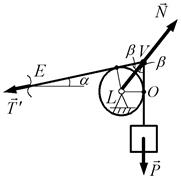
|
|
| а) | б) |
| Рис. 3.7 |
| 
|
| а) | б) |
| Рис. 3.8 |
Таким чином, в цій задачі нитка розрізається в точці 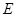 в будь-якому разі, навіть тоді, коли за умовою задачі натяг нитки знаходити не потрібно. Це пояснюється необхідністю виключення з розгляду реакції шарніра
в будь-якому разі, навіть тоді, коли за умовою задачі натяг нитки знаходити не потрібно. Це пояснюється необхідністю виключення з розгляду реакції шарніра 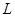 . Обчислення анало-
. Обчислення анало-
гічні наведеним у прикладі 3.1.
Приклад 3.3. До невагомої рами прикладена сила 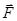 (рис. 3.9, a). Знайти силу, що діє на шарнір
(рис. 3.9, a). Знайти силу, що діє на шарнір 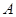 .
.
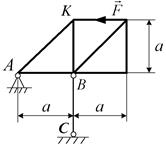 а)
а)
| 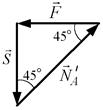 б)
б)
| |
| Рис.3.9 |
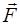 (рис.3.9, a). Знайти силу, що діє на шарнір
(рис.3.9, a). Знайти силу, що діє на шарнір 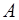 .
.
Розв'язання. Сила, що діє на шарнір 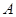 (позначимо її через
(позначимо її через 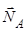 ), не прикладена до рами, тому вона не може бути знайдена з умов рівноваги рами. До рами прикладена реакція шарніра
), не прикладена до рами, тому вона не може бути знайдена з умов рівноваги рами. До рами прикладена реакція шарніра 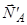 (сили
(сили 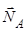 і
і 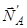 є сили дії і протидії, тобто
є сили дії і протидії, тобто 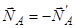 ). Тому спочатку знайдемо реакцію шарніра
). Тому спочатку знайдемо реакцію шарніра 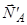 . Рама знаходиться в рівновазі під дією трьох сил: сили
. Рама знаходиться в рівновазі під дією трьох сил: сили 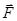 , реакції стрижня
, реакції стрижня 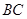 трежня (напрямленої вздовж нього) та реакції шарніра
трежня (напрямленої вздовж нього) та реакції шарніра 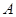 . Оскільки лінії дії сили
. Оскільки лінії дії сили 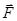 і реакції стрижня перетинаються, то для розв’язання задачі використаємо теорему про три сили. Лінії дії реакції стрижня
і реакції стрижня перетинаються, то для розв’язання задачі використаємо теорему про три сили. Лінії дії реакції стрижня 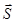 та сили
та сили 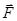 перетинаються в точці
перетинаються в точці 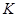 , тому і лінія дії реакції шарніра
, тому і лінія дії реакції шарніра 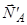 проходить через точку
проходить через точку 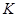 . та точку
. та точку 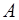 -прикладання сили. Далі будуємо силовий трикутник (рис. 3.9, б), де
-прикладання сили. Далі будуємо силовий трикутник (рис. 3.9, б), де 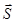 — це реакція стрижня
— це реакція стрижня 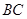 . Із силового трикутника отримаємо:
. Із силового трикутника отримаємо:
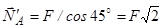 .
.
Остаточно знаходимо
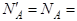
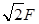 .
.
Напрям сили 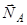 протилежний напряму сили
протилежний напряму сили 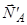 .
.
Приклад 3.4. Знайти зусилля в стрижнях 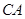 ,
, 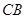 ,
, 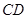 , якщо відома вага вантажа
, якщо відома вага вантажа 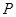 . Площина
. Площина 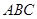 горизонтальна (рис. 3.10).
горизонтальна (рис. 3.10).
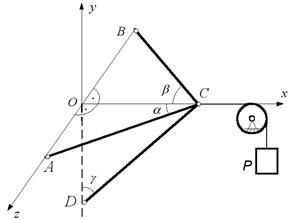
Рис. 3.10
Розв’язання. Будемо розглядати рівновагу шарніра 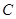 , до якого прикладені реакції стрижнів та натяг нитки. Реакції стрижнів направимо вздовж них однотипно від шарніра
, до якого прикладені реакції стрижнів та натяг нитки. Реакції стрижнів направимо вздовж них однотипно від шарніра 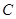 . Натяг нитки
. Натяг нитки 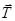 за модулем дорівнює силі
за модулем дорівнює силі 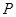 (рис. 3.11). Застосуємо аналітичний метод розв’язання, для чого введемо систему координат
(рис. 3.11). Застосуємо аналітичний метод розв’язання, для чого введемо систему координат 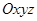 .
.
Рівняння рівноваги мають вигляд::
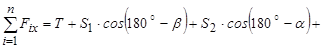
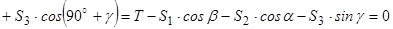 ;
;
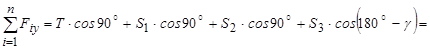
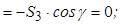
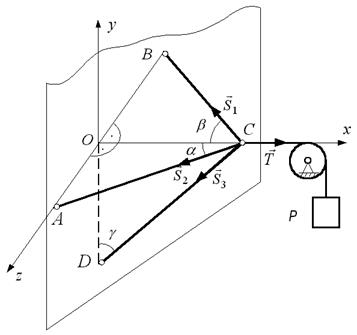
Рис. 3.11
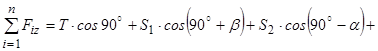
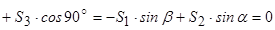 .
.
З другого рівняння знаходимо  . З третього рівняння отримаємо залежність
. З третього рівняння отримаємо залежність 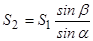 . Після підстановки цього виразу в перше рівняння з урахуванням
. Після підстановки цього виразу в перше рівняння з урахуванням  отримаємо
отримаємо

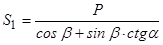 .
.
Далі знаходимо
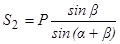 .
.
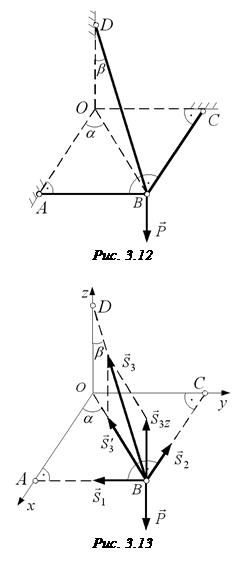 Приклад 3.5. Знайти зусилля в стрижнях АВ, ВС і ВD, якщо до шарніра
Приклад 3.5. Знайти зусилля в стрижнях АВ, ВС і ВD, якщо до шарніра  прикладена вертикальна сила
прикладена вертикальна сила  (рис. 3.12).
(рис. 3.12).
Розв'язання. Введемо декартову систему координат 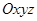 . Переріжемо стрижні біля шарніра
. Переріжемо стрижні біля шарніра  і розглянемо його рівновагу під дією сили
і розглянемо його рівновагу під дією сили 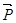 і реакцій
і реакцій 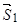 ,
, 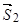 ,
, 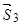
(рис. 3.13), які спрямуємо вздовж відповідних стрижнів однотипно від шарніра  .
.
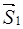 ,
, 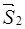 ,
, 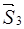 (рис. 3.13), які направимо вздовж відповідних стрижнів однотипно від шарніра
(рис. 3.13), які направимо вздовж відповідних стрижнів однотипно від шарніра  . Маємо збіжну систему сил з трьома невідомими силами, рівняння рівноваги якої містять проекції сил на осі введеної системи координат.
. Маємо збіжну систему сил з трьома невідомими силами, рівняння рівноваги якої містять проекції сил на осі введеної системи координат.
Розглянемо, як при-клад, проектування сили 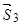 . Для цього використає-мо співвідношення (2.11) – (2.13). Знайдемо
. Для цього використає-мо співвідношення (2.11) – (2.13). Знайдемо 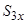 . Спо-чатку спроектуємо силу
. Спо-чатку спроектуємо силу 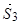 на площину
на площину 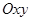 : от-римаємо силу
: от-римаємо силу 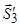 (рис. 3.13), модуль якої дорівнює
(рис. 3.13), модуль якої дорівнює
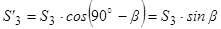 .
.
Далі цей вектор потрібно спроектувати на вісь 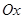 . Знак проекції
. Знак проекції
Рис.3.13 визначаємо безпосередньо з рисунка (" мінус"), тому що кут між вектором 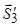 та віссю
та віссю 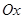 є тупим. Нагадаємо, що при знаходженні кута між вектором та віссю вони повинні бути виведеними з однієї точки. Визначаємо проекцію
є тупим. Нагадаємо, що при знаходженні кута між вектором та віссю вони повинні бути виведеними з однієї точки. Визначаємо проекцію 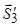 на вісь Ox.
на вісь Ox.
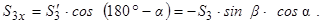
Далі знаходимо 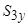 . Для цього на вісь
. Для цього на вісь 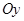 потрібно спроектувати силу
потрібно спроектувати силу 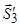 . Знак цієї проекції також від’ємний, тому маємо
. Знак цієї проекції також від’ємний, тому маємо
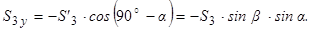
Далі знаходимо проекцію 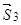 на вісь
на вісь 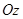 :
:
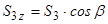 .
.
Запишемо рівняння рівноваги:
 ;
;
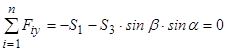
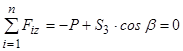
З третього рівняння знайдемо
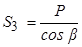 .
.
З першого і другого знаходимо
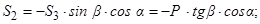
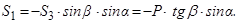
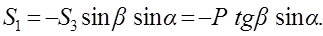
Те, що величини 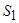 та
та 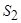 є від’ємними, означає, що сили
є від’ємними, означає, що сили 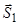 та
та 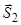 насправді спрямовані в протилежний бік по відношенню до зображених напрямів на рис. 3.13.
насправді спрямовані в протилежний бік по відношенню до зображених напрямів на рис. 3.13.