
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методика розв'язання задач статики при наявності сил тертя ковзання.
|
|
РІВНОВАГА ТІЛ ПРИ НАЯВНОСТІ ТЕРТЯ КОВЗАННЯ

| Якщо опора не є абсолютно гладенькою то має місце не тільки нормальна складова реакції опори 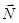 , але й дотична складова , але й дотична складова 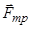 , яку називають силою тертя ковзання (рис. 4.1). Експериментально показано, що сила тертя не може перевищувати певного значення, яке визначають за формулою , яку називають силою тертя ковзання (рис. 4.1). Експериментально показано, що сила тертя не може перевищувати певного значення, яке визначають за формулою
|
| Рис. 4.1 |
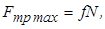 (4.1)
(4.1)
де 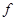 – коефіцієнт пропорційності, який називають коефіцієнтом тертя ковзання.
– коефіцієнт пропорційності, який називають коефіцієнтом тертя ковзання.
Тобто,
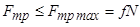 . (4.2)
. (4.2)
При цьому треба враховувати, що у формулі (4.2) 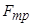 – це модуль сили тертя.
– це модуль сили тертя.
Методика розв'язання задач статики при наявності сил тертя ковзання.
Якщо за умовою задачі відомо, що тіло перебуває у спокої і треба знайти силу тертя ковзання, то її визначають аналогічно будь-якій невідомій силі з умов рівноваги. Для цього зображують силу тертя як дотичну складову реакції опори. Якщо напрям можливого руху тіла в разі відсутності сили тертя є очевидним, то силу тертя доцільно напрямляти в протилежному напрямі (це відображає той факт, що сила тертя ковзання перешкоджає можливому руху). Якщо напрям можливого руху тіла визначити неможливо або складно, то силу тертя спрямовують уздовж дотичної в довільному напрямі (дійсний напрям сили тертя ковзання визначають у процесі розв’язання задачі). Зауважимо, що на цьому етапі розв’язання задачі формули (4.1) та (4.2) не використовують.
У разі, коли треба переконатися, що тіло перебуває в рівновазі, або у випадку, коли мова йде про порушення цього стану, розв’язання задачі слід продовжити, а саме: треба перевірити виконання умови (4.2), або, якщо необхідно, визначити з цієї умови шукану величину (силу тертя ковзання, кут і т.ін.).
У будь-якому разі треба переконатися у виконанні нерівності 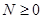 , хоча на першому етапі це свідчить про правильність розв’язання задачі (якщо зазначено, що тіло перебуває в рівновазі, то ця умова вважається виконаною).
, хоча на першому етапі це свідчить про правильність розв’язання задачі (якщо зазначено, що тіло перебуває в рівновазі, то ця умова вважається виконаною).
Приклад 4.1. На шорсткій похилій поверхні (рис. 4.2, а) у стані спокою знаходиться тіло вагою 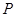 = 10 Н, на яке діє сила Q
= 10 Н, на яке діє сила Q 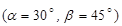 . Визначити:
. Визначити:
1) силу тертя ковзання, коли 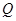 = 7 Н;
= 7 Н;
2) значення сили 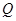 , при яких тіло перебуватиме в стані спокою, якщо коефіцієнт тертя ковзання дорівнює
, при яких тіло перебуватиме в стані спокою, якщо коефіцієнт тертя ковзання дорівнює 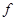 = 0, 05.
= 0, 05.
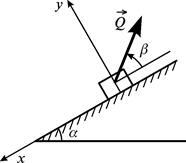
| 
|
| а) | б) |
Рис. 4.2
Розв’язання. Розглядаємо рівновагу тіла, на яке діють сила 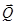 та сила ваги
та сила ваги 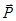 . Зображаємо нормальну складову реакції опори
. Зображаємо нормальну складову реакції опори 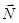 . Оскільки відразу визначити напрям можливого руху тіла не можна, бо він залежить як від величин сил, так і від значень кутів
. Оскільки відразу визначити напрям можливого руху тіла не можна, бо він залежить як від величин сил, так і від значень кутів 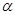 та
та 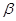 , тому зображаємо силу тертя ковзання
, тому зображаємо силу тертя ковзання 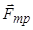 вздовж поверхні в довільному напрямі, наприклад, вниз (рис. 4.2, б).
вздовж поверхні в довільному напрямі, наприклад, вниз (рис. 4.2, б).
Вводимо систему координат 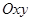 . Для визначення сили
. Для визначення сили 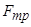 достатньо скористатись одним рівнянням рівноваги, а саме:
достатньо скористатись одним рівнянням рівноваги, а саме:
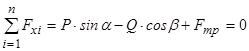 . (4.1)
. (4.1)
Звідси знаходимо:
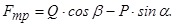 (4.2)
(4.2)
Для заданих величин маємо:
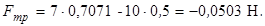
Від’ємний знак величини 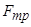 означає, що дійсний напрям сили
означає, що дійсний напрям сили 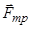 протилежний зображеному на рис. 4.2, б.
протилежний зображеному на рис. 4.2, б.
На цьому перший етап задачі завершено.
Покажемо, що умова (4.2) виконується. Для знаходження нормальної складової реакції шорсткої поверхні 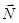 записуємо друге рівняння рівноваги
записуємо друге рівняння рівноваги
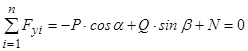 . (4.3)
. (4.3)
Звідси знаходимо
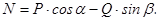 (4.4)
(4.4)
Згідно (4.2) маємо:
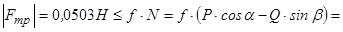
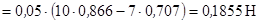 .
.
Розглядаємо другий етап розв’язання задачі. Через те, що мова йде про порушення стану спокою, то суть задачі полягає в дослідженні умови (4.2), а саме:
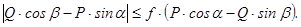 (4.5)
(4.5)
Умову (4.5) можна записати у вигляді:
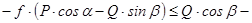
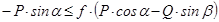 .
.
Звідси
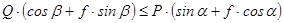 ;
;
(4.6)
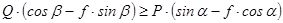 .
.
Для прийнятих даних з (4.6) отримуємо:
 .
.
Зауважимо, що аналогічною розглянутій є наступна постановка задачі: за відомою силою 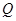 визначити значення кута
визначити значення кута 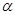 , при якому тіло починає рухатись.
, при якому тіло починає рухатись.
Приклад 4.2. Визначити, при яких значеннях кута 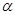 балка вагою Р перебуває в рівновазі. До середини балки прикладена горизонтальна сила
балка вагою Р перебуває в рівновазі. До середини балки прикладена горизонтальна сила 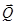 (рис. 4.3, а). Коефіцієнт тертя між балкою та горизонтальною поверхнею дорівнює f. Стіна гладка.
(рис. 4.3, а). Коефіцієнт тертя між балкою та горизонтальною поверхнею дорівнює f. Стіна гладка.
Розв’язання. Зображаємо відомі сили 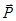 ,
, 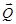 , нормальні складові реакцій в’язей
, нормальні складові реакцій в’язей 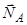 ,
, 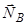 та силу тертя
та силу тертя 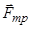 , яку спрямовуємо вздовж осі
, яку спрямовуємо вздовж осі 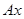 . Початок системи координат приймаємо в точці А. Осі
. Початок системи координат приймаємо в точці А. Осі 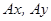 вказано на рис. 4.3, б.
вказано на рис. 4.3, б.

а) б)
Рис. 4.3
Записуємо наступні рівняння рівноваги балки:
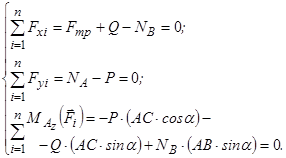 (4.7)
(4.7)
Звідки знаходимо:
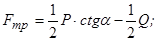
(4.8)
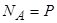 .
.
На цьому завершено перший етап розв’язання задачі.