
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Зведення систем силдо найпростішого виду
|
|
Зведення просторової системи сил, прикладених до твердого тіла, до найпростішого виду полягає у знаходженні однієї сили і однієї пари сил, які є статично еквівалентними цій системі. Шукана сила дорівнює головному вектору 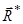 просторової системи сил, прикладеному в довільно вибраному центрі зведення
просторової системи сил, прикладеному в довільно вибраному центрі зведення  . Пара сил має момент
. Пара сил має момент 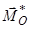 , який дорівнює головному моменту системи сил відносно цього ж центра зведення
, який дорівнює головному моменту системи сил відносно цього ж центра зведення  .
.
Головний вектор 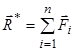 не залежить від вибору центра зведення і є першим статичним інваріантом
не залежить від вибору центра зведення і є першим статичним інваріантом 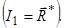
Головний момент 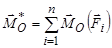 залежить від вибору центра зведення
залежить від вибору центра зведення 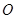 , але його проекція на напрям головного вектора
, але його проекція на напрям головного вектора 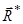 , тобто
, тобто 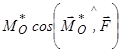 , не залежить від вибору
, не залежить від вибору
центра зведення і її називають другим статичним інваріантом даної системи сил ( ).
).
У випадку зведення просторової системи сил до найпростішого виду можуть зустрітися окремі випадки (див. табл. 6.1).
У таблиці позначено: 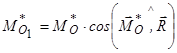 , де
, де 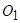 – новий центр зведення, положення якого визначають довжиною відрізка
– новий центр зведення, положення якого визначають довжиною відрізка
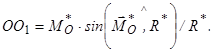
Він перпендикулярний до площини, в якій розміщені головний вектор 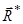 і головний момент
і головний момент 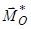 (рис. 6.1).
(рис. 6.1).
Таблиця 6.1
Перший
статичний інваріант
(головний
вектор)
| Головний
момент
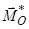
| Другий
статичний
інваріант 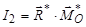
| Випадок зведення системи сил |
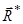 
| 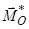 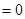
| 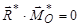
| Система сил еквівалентна нулеві (є зрівноваженою) |
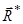 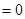
| 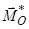 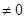
| 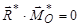
| Пара сил |
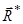 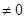
| 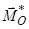 
| 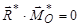
| Рівнодійна, яка прикладена в точці зведення |
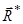 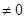
| 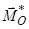 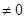
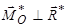
| 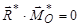
| Рівнодійна, яка зміщена від центра зведення 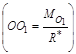
|
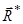 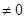
| 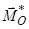 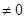
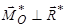
| 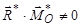
| Динама (силовий гвинт) з силою 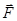 і парою сил з моментом і парою сил з моментом 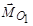 або дві мимобіжні сили або дві мимобіжні сили
|
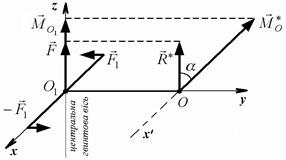
Рис. 6.1
Динама – це сукупність сили 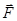 і пари сил
і пари сил 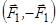 , момент якої
, момент якої 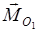 спрямований вздовж лінії дії цієї сили (рис. 6.2).
спрямований вздовж лінії дії цієї сили (рис. 6.2).
Пряму, що проходить через точку 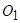 , уздовж якої спрямовані вектори
, уздовж якої спрямовані вектори 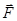 і
і 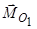 , називають центральною гвинтовою віссю.
, називають центральною гвинтовою віссю.
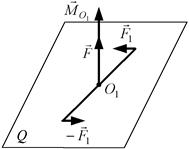
Рис. 6.2
Приклад 6.1. До якого випадку зводиться система сил, якщо її головний вектор 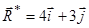 (Н), а головний момент відносно початку координат
(Н), а головний момент відносно початку координат 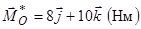 ?
?
Розв’язання. Так як за умовою задачі відомі проекції на осі головного вектора
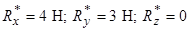
і головного моменту
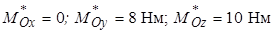 ,
,
визначимо величини головного вектора і головного моменту даної системи сил:
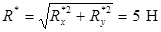 ;
;
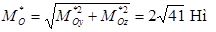 .
.
Так як головний вектор і головний момент відмінні від нуля, то необхідно визначити другий статичний інваріант:
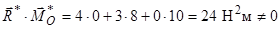 .
.
Отже, дана система сил зводиться до динами (силового гвинта) з головним вектором і головним моментом
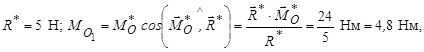
спрямованими вздовж центральної гвинтової осі, яка пара-
лельна лінії дії головного вектора 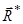 і проходить через точку
і проходить через точку 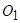 . Положення цієї точки визначають довжиною відрізка
. Положення цієї точки визначають довжиною відрізка
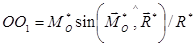 .
.
Оскільки 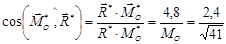 , то
, то
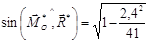 .
.
Тоді 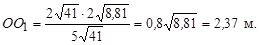
Запишемо рівняння центральної гвинтової осі. Так як
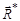 і
і 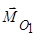 паралельні, то
паралельні, то 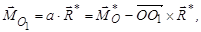
де 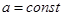 .
.
Тоді в скалярно-аналітичній формі
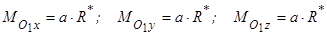 ,
,
тобто
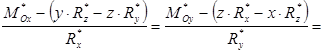
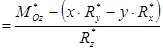 .
.
Після підстановки проекцій векторів головного вектора 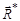 і головного моменту
і головного моменту 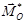 знайдемо
знайдемо
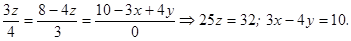
Отже, центральна гвинтова вісь – пряма, яку отримаємо внаслідок перетину площин 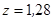 і
і 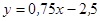 (рис. 6.3).
(рис. 6.3).
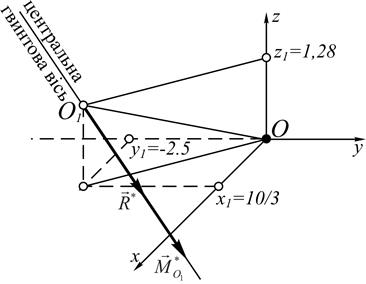
Рис. 6.3
Приклад 6.2. До невагомої пластини  прикладено сили
прикладено сили 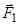 ,
, 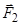 і
і 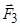 , паралельні осі
, паралельні осі 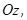 причому
причому 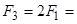
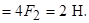 Визначити відстань
Визначити відстань 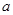 , при якій система сил зводиться до рівнодійної сили, прикладеної у точці
, при якій система сил зводиться до рівнодійної сили, прикладеної у точці 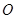 , якщо відстань
, якщо відстань 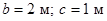 (рис. 6.4).
(рис. 6.4).
Розв’язання. Щоб система сил звелась до рівнодійної, прикладеної у точці 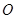 , необхідно, щоб головний момент
, необхідно, щоб головний момент 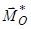 та другий статичний інваріант
та другий статичний інваріант  дорівнювали нулеві, а головний вектор
дорівнювали нулеві, а головний вектор 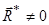 .
.
Визначимо проекції головного вектора 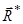 і головного моменту
і головного моменту 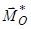 на осі:
на осі:
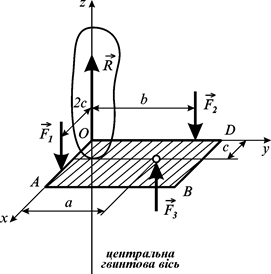
Рис. 6.4
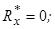
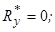
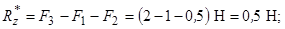
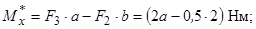

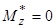 .
.
Тоді головний вектор
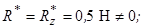
головний момент
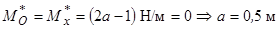 ,
,
а другий статичний інваріант
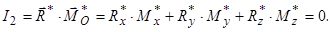
Отже, система сил зводиться до рівнодійної (обведена на рис.6.4), якщо а = 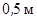 .
.
Приклад 6.3. Визначити модуль сили 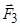 , коли система сил
, коли система сил 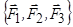 , що прикладена до куба, зводиться до пари сил, якщо відомо:
, що прикладена до куба, зводиться до пари сил, якщо відомо: 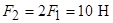 (рис. 6.5).
(рис. 6.5).
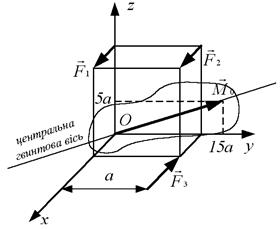
Рис. 6.5
Розв’язання. Для того, щоб система сил звелась до пари сил, необхідно, щоб головний вектор дорівнював нулеві, а головний момент не дорвнював нулеві. За цих умов знаходимо
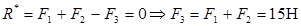 ,
,
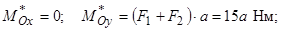
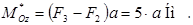
Тоді
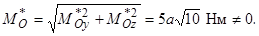
Тобто, головний момент 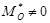 .
.
Отже, якщо сила 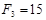 Н, то систему сил можна звести до пари сил.
Н, то систему сил можна звести до пари сил.
Приклад 6.4. На якій відстані 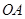 від точки
від точки 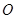 розміщена рівнодійна, якщо головний вектор системи сил
розміщена рівнодійна, якщо головний вектор системи сил 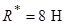 і головний момент
і головний момент 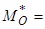 26 Нм взаємно перпендикулярні? (рис. 6.6).
26 Нм взаємно перпендикулярні? (рис. 6.6).
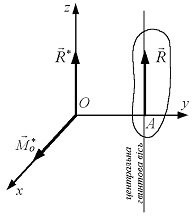
Рис. 6.6
Розв’язання. Дана система сил зводиться до рівнодійної, бо 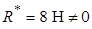 ,
, 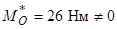 , а другий статичний інваріант
, а другий статичний інваріант
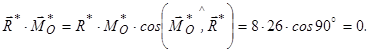
При цьому центральна гвинтова вісь паралельна головному вектору 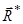 і знаходиться на відстані
і знаходиться на відстані
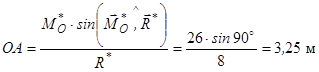 .
.
Ця вісь зміщена вправо, тому що головний вектор 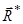 повинен повертатись відносно старого центра зведення (точки
повинен повертатись відносно старого центра зведення (точки 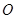 ) проти ходу годинникової стрілки, бо
) проти ходу годинникової стрілки, бо 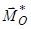 спрямований на нас.
спрямований на нас.
Приклад 6.5. Головний вектор 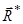 іголовний момент
іголовний момент 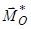 системи сил розміщені у площині
системи сил розміщені у площині 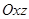 . Визначити відстань
. Визначити відстань 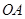 до центральної гвинтової осі, якщо відомі
до центральної гвинтової осі, якщо відомі 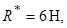
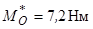 і кут між
і кут між 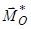 і віссю
і віссю 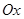 дорівнює
дорівнює 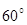 (рис. 6.7).
(рис. 6.7).
Розв’язання. Відрізок 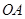 перпендикулярний до головного вектора
перпендикулярний до головного вектора 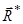 і головного моменту
і головного моменту 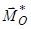 , які розміщені у площині
, які розміщені у площині 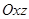 . Отже, відрізок
. Отже, відрізок 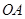 лежить на осі
лежить на осі 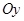 і зміщений вправо.
і зміщений вправо.
Момент зведеної пари сил
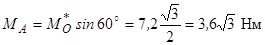 ,
,
а відстань 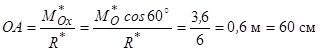 .
.
Центральна гвинтова лінія паралельна головному вектору 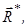 тобто осі
тобто осі 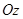 , і проходить через точку
, і проходить через точку 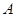 (рис. 6.7).
(рис. 6.7).
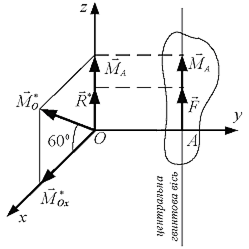
Рис. 6.7