Центр ваги твердого тіла

На всі частинки тіла, що знаходиться поблизу поверхні Землі, діє сила ваги. Якщо тіло розбити на елементарні частини, сили ваг яких позначити як 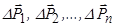(рис. 7.2), і врахувати, що розміри тіла є незначними порівняно з розмірами Землі, то сили ваг елементарних частин тіла з достатньо великою точністю утворюють систему паралельних сил.

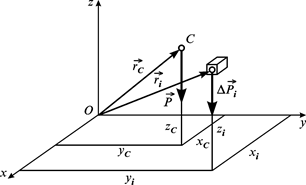
Рис. 7.2

Рівнодійна сил ваг окремих частин тіла називається силою ваги тіла.

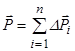. (7.7)

Сили ваг окремих частин тіла 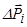паралельні і напрямлені в один бік, тому з виразу (7.3) можна отримати

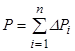. (7.8)

Тобто, вага тіла дорівнює сумі ваг окремих його частин.

Центр паралельних сил ваг окремих частин тіла називається центром ваги тіла. На рис. 7.2 центр ваги тіла позначено буквою С.

Радіус-вектор центра ваги 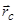визначається на основі формули (7.5) у вигляді

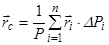. (7.9)

Переходячи у виразі (7.9) до границі при 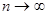і припускаючи, що розміри всіх елементарних частин прямують до нуля, дістанемо

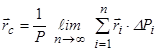. (7.10)

Границя суми у цьому виразі є інтегралом, поширеному на об’єм тіла. У результаті отримаємо

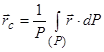. (7.11)

На основі формули (7.9) в проекціях на координатні осі отримаємо:

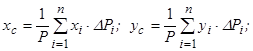
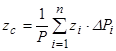, (7.12)

а на основі (7.11) дістанемо:

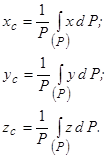(7.13)

Розглянемо деякі часткові випадки.

7.2.1 Центр ваги однорідного тіла (центр ваги об’єму)

Для однорідних тіл питома вага 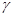є величиною сталою по об’єму.

Вага тіла дорівнює:

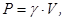(7.14)

де 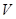— об’єм всього тіла.

Вага частини тіла дорівнює

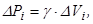(7.15)

де 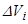— об’єм частини тіла.

Підставивши (7.14) і (7.15) в (7.9¸ 7.13), отримаємо формули, які визначають координати центра ваги однорідного тіла.

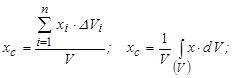
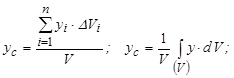(7.16)

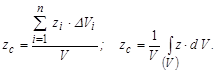
7.2.2 Центр ваги площі однорідного плоского тіла
(центр ваги площі)

Розглядається однорідне плоске тіло товщиною , розміщене в площині (рис. 7.3)

Вага такого тіла і ваги окремих його частин дорівнюють:

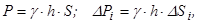(7.17)

де 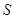— площа тіла; 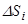— площа окремої його частини.

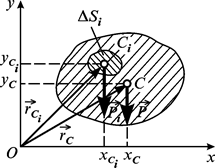
Рис. 7.3

Підставивши (7.17) в (7.9)¸ (7.13) отримаємо формули, які визначають координати центра ваги однорідного плоского тіла:

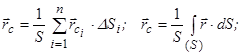
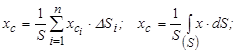
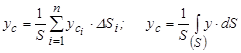, (7.18)

де 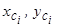— координати центра ваги і -ої частинки.

Сума добутків площі кожного елемента плоскої фігури на його відстань до деякої осі, яка лежить у площині фігури, називається статичним моментом плоскої фігури відносно цієї осі.

Статичні моменти (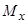 і 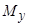) плоскої фігури (рис. 7.3) відносно осей 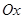і 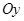відповідно дорівнюють:

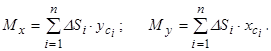(7.19)

Підставивши вирази (7.19) в (7.18), отримаємо для координат центра ваги плоскої фігури такі формули:

(7.20)

За цими формулами обчислюють координати центра ваги плоскої фігури, якщо відомі її статичні моменти 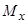і .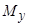

7.2.3 Центр ваги однорідного лінійного тіла
(центр ваги лінії)

Позначивши через 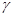вагу одиниці довжини однорідного лінійного тіла, його вагу і вагу його окремої частини визначимо за формулами:

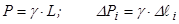, (7.21)

де: 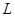— довжина тіла; 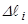— довжина 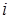-го елемента.

Підставивши (7.21) у вирази (7.9)¸ (7.13), отримаємо формули, які визначають координати центра ваги лінійного однорідного тіла (наприклад, дроту, стрижневої конструкції і т.ін., рис. 7.4)

(7.14)

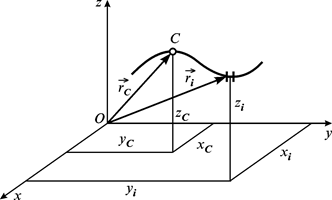
Рис. 7.4